Related Research Articles
Control theory in control systems engineering is a subfield of mathematics that deals with the control of continuously operating dynamical systems in engineered processes and machines. The objective is to develop a control model for controlling such systems using a control action in an optimum manner without delay or overshoot and ensuring control stability.
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences and engineering disciplines, as well as in the social sciences.

In signal processing, a signal is a function that conveys information about a phenomenon. In electronics and telecommunications, it refers to any time varying voltage, current or electromagnetic wave that carries information. A signal may also be defined as an observable change in a quality such as quantity.

Computer simulation is the process of mathematical modelling, performed on a computer, which is designed to predict the behaviour of and/or the outcome of a real-world or physical system. Since they allow to check the reliability of chosen mathematical models, computer simulations have become a useful tool for the mathematical modeling of many natural systems in physics, astrophysics, climatology, chemistry, biology and manufacturing, as well as human systems in economics, psychology, social science, health care and engineering. Simulation of a system is represented as the running of the system's model. It can be used to explore and gain new insights into new technology and to estimate the performance of systems too complex for analytical solutions.
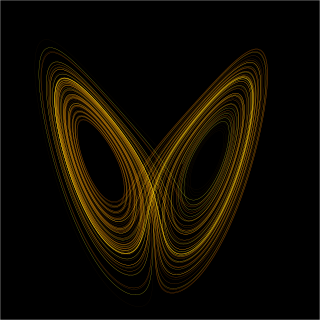
Dynamical systems theory is an area of mathematics used to describe the behavior of the complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a least action principle. When difference equations are employed, the theory is called discrete dynamical systems. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed operators, such as differential-difference equations.
Telecommunications traffic engineering, teletraffic engineering, or traffic engineering is the application of traffic engineering theory to telecommunications. Teletraffic engineers use their knowledge of statistics including queuing theory, the nature of traffic, their practical models, their measurements and simulations to make predictions and to plan telecommunication networks such as a telephone network or the Internet. These tools and knowledge help provide reliable service at lower cost.
A state variable is one of the set of variables that are used to describe the mathematical "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour in the absence of any external forces affecting the system. Models that consist of coupled first-order differential equations are said to be in state-variable form.
A discrete-event simulation (DES) models the operation of a system as a (discrete) sequence of events in time. Each event occurs at a particular instant in time and marks a change of state in the system. Between consecutive events, no change in the system is assumed to occur; thus the simulation time can directly jump to the occurrence time of the next event, which is called next-event time progression.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.
Polynomial chaos (PC), also called Wiener chaos expansion, is a non-sampling-based method to determine evolution of uncertainty in a dynamical system when there is probabilistic uncertainty in the system parameters. PC was first introduced by Norbert Wiener where Hermite polynomials were used to model stochastic processes with Gaussian random variables. It can be thought of as an extension of Volterra's theory of nonlinear functionals for stochastic systems. According to Cameron and Martin such an expansion converges in the sense for any arbitrary stochastic process with finite second moment. This applies to most physical systems.

EcosimPro is a simulation tool developed by Empresarios Agrupados A.I.E for modelling simple and complex physical processes that can be expressed in terms of Differential algebraic equations or Ordinary differential equations and Discrete event simulation.
DEVS abbreviating Discrete Event System Specification is a modular and hierarchical formalism for modeling and analyzing general systems that can be discrete event systems which might be described by state transition tables, and continuous state systems which might be described by differential equations, and hybrid continuous state and discrete event systems. DEVS is a timed event system.
Stochastic control or stochastic optimal control is a sub field of control theory that deals with the existence of uncertainty either in observations or in the noise that drives the evolution of the system. The system designer assumes, in a Bayesian probability-driven fashion, that random noise with known probability distribution affects the evolution and observation of the state variables. Stochastic control aims to design the time path of the controlled variables that performs the desired control task with minimum cost, somehow defined, despite the presence of this noise. The context may be either discrete time or continuous time.

Creating a cellular model has been a particularly challenging task of systems biology and mathematical biology. It involves developing efficient algorithms, data structures, visualization and communication tools to orchestrate the integration of large quantities of biological data with the goal of computer modeling.

Traffic simulation or the simulation of transportation systems is the mathematical modeling of transportation systems through the application of computer software to better help plan, design, and operate transportation systems. Simulation of transportation systems started over forty years ago, and is an important area of discipline in traffic engineering and transportation planning today. Various national and local transportation agencies, academic institutions and consulting firms use simulation to aid in their management of transportation networks.
MLDesigner is an integrated modeling and simulation tool for the design and analysis of complex embedded and networked systems. MLDesigner speeds up modeling, simulation and analysis of discrete event, discrete time and continuous time systems concerning architecture, function and performance. The tools is based on ideas of the "Ptolemy Project", done at the University if California Berkeley. MLDesigner is developed by MLDesign Technologies Inc. Palo Alto, CA, USA in collaboration with Mission Level Design GmbH, Ilmenau, Germany.
In mathematical modeling, deterministic simulations contain no random variables and no degree of randomness, and consist mostly of equations, for example difference equations. These simulations have known inputs and they result in a unique set of outputs. Contrast stochastic (probability) simulation, which includes random variables.
Design of robust and reliable networks and network services relies on an understanding of the traffic characteristics of the network. Throughout history, different models of network traffic have been developed and used for evaluating existing and proposed networks and services.
System identification is a method of identifying or measuring the mathematical model of a system from measurements of the system inputs and outputs. The applications of system identification include any system where the inputs and outputs can be measured and include industrial processes, control systems, economic data, biology and the life sciences, medicine, social systems and many more.
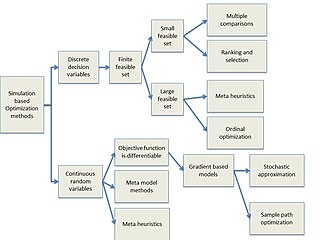
Simulation-based optimization integrates optimization techniques into simulation analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate.
References
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Flood, J.E. Telecommunications Switching, Traffic and Networks, Chapter 4: Telecommunications Traffic, New York: Prentice-Hall, 1998.
- 1 2 3 4 5 6 7 8 Penttinen A., Chapter 9 – Simulation, Lecture Notes: S-38.145 - Introduction to Teletraffic Theory, Helsinki University of Technology, Fall 1999.
- ↑ Kennedy I. G., Traffic Simulation, School of Electrical and Information Engineering, University of the Witwatersrand, 2003.
- ↑ Akimaru H., Kawashima K., Teletraffic – Theory and Applications, Springer-Verlag London, 2nd Edition, 1999, pg 6