New digraph reconstruction conjecture

Last updated
Unsolved problem in mathematics:

Are digraphs uniquely determined by their subgraphs and some in-degree data?

Contents

(more unsolved problems in mathematics)

The reconstruction conjecture of Stanisław Ulam is one of the best-known open problems in graph theory. Using the terminology of Frank Harary [1] it can be stated as follows: If G and H are two graphs on at least three vertices and ƒ is a bijection from V(G) to V(H) such that G\{v} and H\{ƒ(v)} are isomorphic for all vertices v in V(G), then G and H are isomorphic.

In 1964 Harary [2] extended the reconstruction conjecture to directed graphs on at least five vertices as the so-called digraph reconstruction conjecture. Many results supporting the digraph reconstruction conjecture appeared between 1964 and 1976. However, this conjecture was proved to be false when P. K. Stockmeyer discovered several infinite families of counterexample pairs of digraphs (including tournaments) of arbitrarily large order. [3] [4] [5] The falsity of the digraph reconstruction conjecture caused doubt about the reconstruction conjecture itself. Stockmeyer even observed that “perhaps the considerable effort being spent in attempts to prove the (reconstruction) conjecture should be balanced by more serious attempts to construct counterexamples.” [3]

In 1979, Ramachandran revived the digraph reconstruction conjecture in a slightly weaker form called the new digraph reconstruction conjecture. In a digraph, the number of arcs incident from (respectively, to) a vertex v is called the outdegree (indegree) of v and is denoted by od(v) (respectively, id(v)). The new digraph conjecture may be stated as follows: [6] [7]

If D and E are any two digraphs and ƒ is a bijection from V(D) to V(E) such that D\{v} and E\{ƒ(v)} are isomorphic and (od(v),id(v)) = (od(ƒ(v)),id(ƒ(v))) for all v in V(D), then D and E are isomorphic.

The new digraph reconstruction conjecture reduces to the reconstruction conjecture in the undirected case, because if all the vertex-deleted subgraphs of two graphs are isomorphic, then the corresponding vertices must have the same degree. Thus, the new digraph reconstruction conjecture is stronger than the reconstruction conjecture, but weaker than the disproved digraph reconstruction conjecture. Several families of digraphs have been shown to satisfy the new digraph reconstruction conjecture and these include all the digraphs in the known counterexample pairs to the digraph reconstruction conjecture.

Reductions

Present status

As of 2024, no counterexample to the new digraph reconstruction conjecture is known. This conjecture is now also known as the degree associated reconstruction conjecture.

Related Research Articles

<span class="mw-page-title-main">Graph theory</span> Area of discrete mathematics

In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics.

<span class="mw-page-title-main">Kuratowski's theorem</span> On forbidden subgraphs in planar graphs

In graph theory, Kuratowski's theorem is a mathematical forbidden graph characterization of planar graphs, named after Kazimierz Kuratowski. It states that a finite graph is planar if and only if it does not contain a subgraph that is a subdivision of or of .

<span class="mw-page-title-main">Graph isomorphism</span> Bijection between the vertex set of two graphs

In graph theory, an isomorphism of graphsG and H is a bijection between the vertex sets of G and H

Informally, the reconstruction conjecture in graph theory says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.

This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).

<span class="mw-page-title-main">Critical graph</span> Undirected graph

In graph theory, a critical graph is an undirected graph all of whose proper subgraphs have smaller chromatic number. In such a graph, every vertex or edge is a critical element, in the sense that its deletion would decrease the number of colors needed in a graph coloring of the given graph. The decrease in the number of colors cannot be by more than one.

In graph theory, the strong perfect graph theorem is a forbidden graph characterization of the perfect graphs as being exactly the graphs that have neither odd holes nor odd antiholes. It was conjectured by Claude Berge in 1961. A proof by Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas was announced in 2002 and published by them in 2006.

<span class="mw-page-title-main">Complement graph</span> Graph with same nodes but opposite connections as another

In the mathematical field of graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two distinct vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there.

<span class="mw-page-title-main">Wheel graph</span> Cycle graph plus universal vertex

In the mathematical discipline of graph theory, a wheel graph is a graph formed by connecting a single universal vertex to all vertices of a cycle. A wheel graph with n vertices can also be defined as the 1-skeleton of an (n – 1)-gonal pyramid. Some authors write Wn to denote a wheel graph with n vertices ; other authors instead use Wn to denote a wheel graph with n + 1 vertices, which is formed by connecting a single vertex to all vertices of a cycle of length n. The rest of this article uses the former notation.

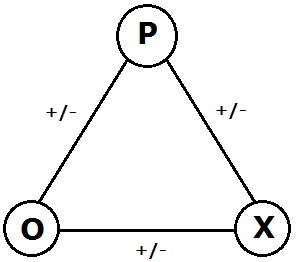
<span class="mw-page-title-main">Signed graph</span> Graph with sign-labeled edges

In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign.

<span class="mw-page-title-main">Graph factorization</span>

In graph theory, a factor of a graph G is a spanning subgraph, i.e., a subgraph that has the same vertex set as G. A k-factor of a graph is a spanning k-regular subgraph, and a k-factorization partitions the edges of the graph into disjoint k-factors. A graph G is said to be k-factorable if it admits a k-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a k-regular graph is a proper edge coloring with k colors. A 2-factor is a collection of cycles that spans all vertices of the graph.

<span class="mw-page-title-main">Circulant graph</span> Undirected graph acted on by a vertex-transitive cyclic group of symmetries

In graph theory, a circulant graph is an undirected graph acted on by a cyclic group of symmetries which takes any vertex to any other vertex. It is sometimes called a cyclic graph, but this term has other meanings.

<span class="mw-page-title-main">Factor-critical graph</span> Graph of n vertices with a perfect matching for every subgraph of n-1 vertices

In graph theory, a mathematical discipline, a factor-critical graph is a graph with n vertices in which every subgraph of n − 1 vertices has a perfect matching.

<span class="mw-page-title-main">Hedetniemi's conjecture</span> Conjecture in graph theory

In graph theory, Hedetniemi's conjecture, formulated by Stephen T. Hedetniemi in 1966, concerns the connection between graph coloring and the tensor product of graphs. This conjecture states that

In graph theory, Vizing's conjecture concerns a relation between the domination number and the cartesian product of graphs. This conjecture was first stated by Vadim G. Vizing (1968), and states that, if γ(G) denotes the minimum number of vertices in a dominating set for the graph G, then

<span class="mw-page-title-main">Directed graph</span> Graph with oriented edges

In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by directed edges, often called arcs.

<span class="mw-page-title-main">Polyhedral graph</span> Graph made from vertices and edges of a convex polyhedron

In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.

<span class="mw-page-title-main">Caterpillar tree</span> Tree graph with all nodes within distance 1 from central path

In graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices are within distance 1 of a central path.

<span class="mw-page-title-main">Pancyclic graph</span>

In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length.

References

  1. ↑ Harary, Frank (1969), Graph Theory, Reading, Mass.: Addison-Wesley, MR   0256911 .
  2. ↑ Harary, Frank (1964), "On the reconstruction of a graph from a collection of subgraphs", in Fiedler, M. (ed.), Theory of Graphs and its Applications (Proc. Sympos. Smolenice, 1963), Publ. House Czechoslovak Acad. Sci., Prague, pp. 47–52, MR   0175111
  3. 1 2 Stockmeyer, Paul K. (1977), "The falsity of the reconstruction conjecture for tournaments", Journal of Graph Theory , 1 (1): 19–25, doi:10.1002/jgt.3190010108, MR   0453584 . Erratum, J. Graph Th.62 (2): 199–200, 2009, doi : 10.1002/jgt.20398, MR 2555098.
  4. ↑ Stockmeyer, Paul K. (1981), "A census of nonreconstructible digraphs. I. Six related families", Journal of Combinatorial Theory , Series B, 31 (2): 232–239, doi:10.1016/S0095-8956(81)80027-5, MR   0630985 .
  5. ↑ Stockmeyer, Paul K. (1991), A census of nonreconstructible digraphs II: A family of tournaments, Preprint.
  6. ↑ Ramachandran, S. (1979), "A digraph reconstruction conjecture", Graph Theory Newsletter, 8 (4), Western Michigan University.
  7. ↑ Ramachandran, S. (1981), "On a new digraph reconstruction conjecture", Journal of Combinatorial Theory , Series B, 31 (2): 143–149, doi: 10.1016/S0095-8956(81)80019-6 , MR   0630977 .
  8. ↑ Ramachandran, S; Monikandan, S (2006), "All Digraphs are N-reconstructible if all Digraphs with 2-connected underlying Graphs are N-reconstructible", Utilitas Mathematica, 71, UTIL MATH PUBL INC: 225–234, MR   2278835
  9. ↑ Ramachandran, S (2012), "Sufficient Conditions For The N-Reconstructibility Of All Digraphs", Utilitas Mathematica, 88, UTIL MATH PUBL INC: 183–188, MR   2975831
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.