Related Research Articles
In computational mathematics, an iterative method is a mathematical procedure that uses an initial value to generate a sequence of improving approximate solutions for a class of problems, in which the n-th approximation is derived from the previous ones.

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt at finding approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.
In numerical analysis, Newton's method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots of a real-valued function. The most basic version starts with a real-valued function f, its derivative f′, and an initial guess x0 for a root of f. If f satisfies certain assumptions and the initial guess is close, then

In computer animation and robotics, inverse kinematics is the mathematical process of calculating the variable joint parameters needed to place the end of a kinematic chain, such as a robot manipulator or animation character's skeleton, in a given position and orientation relative to the start of the chain. Given joint parameters, the position and orientation of the chain's end, e.g. the hand of the character or robot, can typically be calculated directly using multiple applications of trigonometric formulas, a process known as forward kinematics. However, the reverse operation is, in general, much more challenging.
In numerical analysis, inverse iteration is an iterative eigenvalue algorithm. It allows one to find an approximate eigenvector when an approximation to a corresponding eigenvalue is already known. The method is conceptually similar to the power method. It appears to have originally been developed to compute resonance frequencies in the field of structural mechanics.
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of an iterative method. Arnoldi finds an approximation to the eigenvalues and eigenvectors of general matrices by constructing an orthonormal basis of the Krylov subspace, which makes it particularly useful when dealing with large sparse matrices.
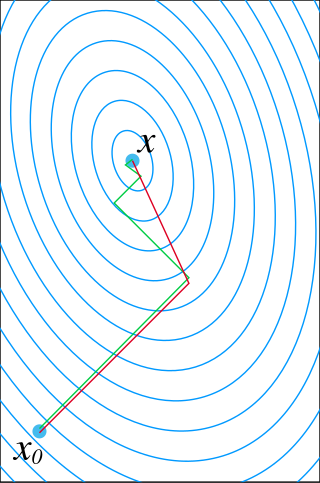
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.
In numerical analysis, a multigrid method is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners.
In linear algebra, the order-rKrylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A, that is,
In mathematics, the generalized minimal residual method (GMRES) is an iterative method for the numerical solution of an indefinite nonsymmetric system of linear equations. The method approximates the solution by the vector in a Krylov subspace with minimal residual. The Arnoldi iteration is used to find this vector.
In mathematics, preconditioning is the application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solving methods. Preconditioning is typically related to reducing a condition number of the problem. The preconditioned problem is then usually solved by an iterative method.
Quasi-Newton methods are methods used to either find zeroes or local maxima and minima of functions, as an alternative to Newton's method. They can be used if the Jacobian or Hessian is unavailable or is too expensive to compute at every iteration. The "full" Newton's method requires the Jacobian in order to search for zeros, or the Hessian for finding extrema. Some iterative methods that reduce to Newton's method, such as SLSQP, may be considered quasi-Newtonian.
In computational mathematics, a matrix-free method is an algorithm for solving a linear system of equations or an eigenvalue problem that does not store the coefficient matrix explicitly, but accesses the matrix by evaluating matrix-vector products. Such methods can be preferable when the matrix is so big that storing and manipulating it would cost a lot of memory and computing time, even with the use of methods for sparse matrices. Many iterative methods allow for a matrix-free implementation, including:
In numerical analysis, Broyden's method is a quasi-Newton method for finding roots in k variables. It was originally described by C. G. Broyden in 1965.

Lis is a scalable parallel software library for solving discretized linear equations and eigenvalue problems that mainly arise in the numerical solution of partial differential equations by using iterative methods. Although it is designed for parallel computers, the library can be used without being conscious of parallel processing.
In numerical linear algebra, the biconjugate gradient stabilized method, often abbreviated as BiCGSTAB, is an iterative method developed by H. A. van der Vorst for the numerical solution of nonsymmetric linear systems. It is a variant of the biconjugate gradient method (BiCG) and has faster and smoother convergence than the original BiCG as well as other variants such as the conjugate gradient squared method (CGS). It is a Krylov subspace method. Unlike the original BiCG method, it doesn't require multiplication by the transpose of the system matrix.
SLEPc is a software library for the parallel computation of eigenvalues and eigenvectors of large, sparse matrices. It can be seen as a module of PETSc that provides solvers for different types of eigenproblems, including linear and nonlinear, as well as the SVD. Recent versions also include support for matrix functions. It uses the MPI standard for parallelization. Both real and complex arithmetic are supported, with single, double and quadruple precision.
The following is a timeline of numerical analysis after 1945, and deals with developments after the invention of the modern electronic computer, which began during Second World War. For a fuller history of the subject before this period, see timeline and history of mathematics.
In mathematics, Anderson acceleration, also called Anderson mixing, is a method for the acceleration of the convergence rate of fixed-point iterations. Introduced by Donald G. Anderson, this technique can be used to find the solution to fixed point equations often arising in the field of computational science.
References
- ↑ Knoll, D.A.; Keyes, D.E. (2004). "Jacobian-free Newton–Krylov methods: a survey of approaches and applications". Journal of Computational Physics. 193 (2): 357. CiteSeerX 10.1.1.636.3743 . doi:10.1016/j.jcp.2003.08.010.
- ↑ Kelley, C.T. (2003). Solving nonlinear equations with Newton's method (1 ed.). SIAM.