A histogram is an accurate representation of the distribution of numerical data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson. It differs from a bar graph, in the sense that a bar graph relates two variables, but a histogram relates only one. To construct a histogram, the first step is to "bin" the range of values—that is, divide the entire range of values into a series of intervals—and then count how many values fall into each interval. The bins are usually specified as consecutive, non-overlapping intervals of a variable. The bins (intervals) must be adjacent, and are often of equal size.
Pearson's chi-squared test (χ2) is a statistical test applied to sets of categorical data to evaluate how likely it is that any observed difference between the sets arose by chance. It is the most widely used of many chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900. In contexts where it is important to improve a distinction between the test statistic and its distribution, names similar to Pearson χ-squared test or statistic are used.
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given random-sample-based statistic. If an arbitrarily large number of samples, each involving multiple observations, were separately used in order to compute one value of a statistic for each sample, then the sampling distribution is the probability distribution of the values that the statistic takes on. In many contexts, only one sample is observed, but the sampling distribution can be found theoretically.
The t-test is any statistical hypothesis test in which the test statistic follows a Student's t-distribution under the null hypothesis.

The standard error (SE) of a statistic is the standard deviation of its sampling distribution or an estimate of that standard deviation. If the parameter or the statistic is the mean, it is called the standard error of the mean (SEM).
Sample size determination is the act of choosing the number of observations or replicates to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample. In practice, the sample size used in a study is usually determined based on the cost, time, or convenience of collecting the data, and the need for it to offer sufficient statistical power. In complicated studies there may be several different sample sizes: for example, in a stratified survey there would be different sizes for each stratum. In a census, data is sought for an entire population, hence the intended sample size is equal to the population. In experimental design, where a study may be divided into different treatment groups, there may be different sample sizes for each group.
The Western Electric rules are decision rules in statistical process control for detecting out-of-control or non-random conditions on control charts. Locations of the observations relative to the control chart control limits and centerline indicate whether the process in question should be investigated for assignable causes. The Western Electric rules were codified by a specially-appointed committee of the manufacturing division of the Western Electric Company and appeared in the first edition of a 1956 handbook, that became a standard text of the field. Their purpose was to ensure that line workers and engineers interpret control charts in a uniform way.

In statistical process monitoring (SPM), the and R chart is a type of scheme, popularly known as control chart, used to monitor the mean and range of a normally distributed variables simultaneously, when samples are collected at regular intervals from a business or industrial process.. It is often used to monitor the variables data but the performance of the and R chart may suffer when the normality assumption is not valid. This is connected traditional statistical quality control (SQC) and statistical process control (SPC). However, Woodall noted that "I believe that the use of control charts and other monitoring methods should be referred to as “statistical process monitoring,” not “statistical process control (SPC).”"

In statistical quality control, the p-chart is a type of control chart used to monitor the proportion of nonconforming units in a sample, where the sample proportion nonconforming is defined as the ratio of the number of nonconforming units to the sample size, n.
Natural process variation, sometimes just called process variation, is the statistical description of natural fluctuations in process outputs.

In statistics, bootstrapping is any test or metric that relies on random sampling with replacement. Bootstrapping allows assigning measures of accuracy to sample estimates. This technique allows estimation of the sampling distribution of almost any statistic using random sampling methods. Generally, it falls in the broader class of resampling methods.
The combination of quality control and genetic algorithms led to novel solutions of complex quality control design and optimization problems. Quality control is a process by which entities review the quality of all factors involved in production. Quality is the degree to which a set of inherent characteristics fulfils a need or expectation that is stated, general implied or obligatory. Genetic algorithms are search algorithms, based on the mechanics of natural selection and natural genetics.
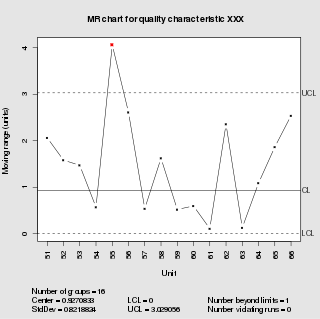
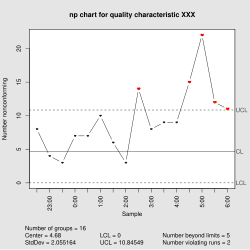
In statistical quality control, the individual/moving-range chart is a type of control chart used to monitor variables data from a business or industrial process for which it is impractical to use rational subgroups.
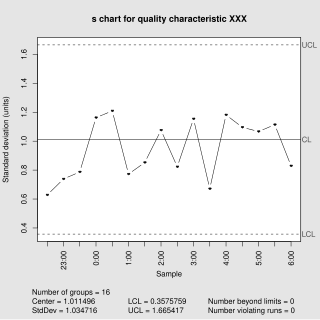
In statistical quality control, the and s chart is a type of control chart used to monitor variables data when samples are collected at regular intervals from a business or industrial process. This is connected traditional statistical quality control (SQC) and statistical process control (SPC). However, Woodall noted that "I believe that the use of control charts and other monitoring methods should be referred to as “statistical process monitoring,” not “statistical process control (SPC).”"
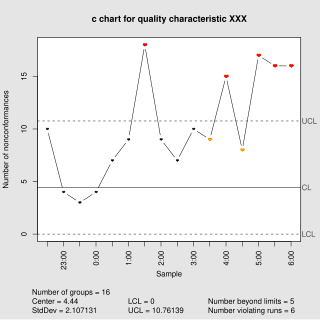
In statistical quality control, the c-chart is a type of control chart used to monitor "count"-type data, typically total number of nonconformities per unit. It is also occasionally used to monitor the total number of events occurring in a given unit of time.
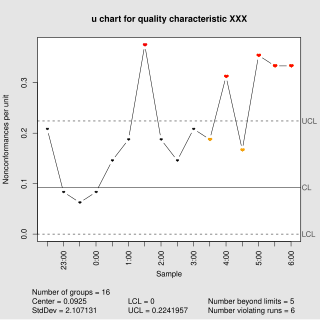
In statistical quality control, the u-chart is a type of control chart used to monitor "count"-type data where the sample size is greater than one, typically the average number of nonconformities per unit.

In statistical quality control, the EWMA chart is a type of control chart used to monitor either variables or attributes-type data using the monitored business or industrial process's entire history of output. While other control charts treat rational subgroups of samples individually, the EWMA chart tracks the exponentially-weighted moving average of all prior sample means. EWMA weights samples in geometrically decreasing order so that the most recent samples are weighted most highly while the most distant samples contribute very little.
Acceptance sampling uses statistical sampling to determine whether to accept or reject a production lot of material. It has been a common quality control technique used in industry. It is usually done as products leaves the factory, or in some cases even within the factory. Most often a producer supplies a consumer a number of items and a decision to accept or reject the items is made by determining the number of defective items in a sample from the lot. The lot is accepted if the number of defects falls below where the acceptance number or otherwise the lot is rejected.
A variables sampling plan is an acceptance sampling technique. Plans for variables are intended for quality characteristics that are measured in a continuous scale. This plan requires the knowledge of the statistical model e.g. normal distribution. The historical evolution of this technique dates back to the seminal work of Wallis (1943). The purpose of a plan for variables is to assess whether the process is operating far enough from the specification limit. Plans for variables may produce a similar OC curve to attribute plans with significantly less sample size.