Null move

Last updated

In game theory, a null move or pass is a decision by a player to not make a move when it is that player's turn to move. Even though null moves are against the rules of many games, they are often useful to consider when analyzing these games. Examples of this include the analysis of zugzwang (a situation in chess or other games in which a null move, if it were allowed, would be better than any other move), [1] and the null-move heuristic in game tree analysis (a method of pruning game trees involving making a null move and then searching to a lower depth). [2]

Game theory is the study of mathematical models of strategic interaction in between rational decision-makers. It has applications in all fields of social science, as well as in logic and computer science. Originally, it addressed zero-sum games, in which each participant's gains or losses are exactly balanced by those of the other participants. Today, game theory applies to a wide range of behavioral relations, and is now an umbrella term for the science of logical decision making in humans, animals, and computers.

Zugzwang is a situation found in chess and other games wherein one player is put at a disadvantage because they must make a move when they would prefer to pass and not move. The fact that the player is compelled to move means that their position will become significantly weaker. A player is said to be "in zugzwang" when any possible move will worsen their position.

In computer chess programs, the null-move heuristic is a heuristic technique used to enhance the speed of the alpha-beta pruning algorithm.

The reason a reduced-depth null move is effective in game tree alpha-beta search reduction is that tactical threats tend to show up very quickly, in just one or two moves. If the opponent has no tactical threats revealed by null move search, the position may be good enough to exceed the best result obtainable in another branch of the tree (i.e. "beta"), so that no further search need be done from the current node, and the result from the null move can be returned as the search value. Even if the null move search value doesn't exceed beta, the returned value may set a higher floor on the valuation of the position than the present alpha, so more cutoffs will occur at descendant sibling nodes from the position.

The underlying assumption is that at least some legal move available to the player on move at the node is better than no move at all. In the case of the player on move being in zugswang, that assumption is false, and the null move result is invalid (in that case, it actually sets a ceiling on the value of the position). Therefore it is necessary to have logic to exclude null moves at nodes in the tree where zugswang is possible. In chess, zugawang positions can occur in king and pawn endgames, and sometimes in end games that include other pieces as well.

Related Research Articles

Minimax is a decision rule used in artificial intelligence, decision theory, game theory, statistics and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin"—to maximize the minimum gain. Originally formulated for two-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.

Computer chess computer hardware and software capable of playing chess

Computer chess includes both hardware and software capable of playing chess. Computer chess provides opportunities for players to practice even in the absence of human opponents, and also provides opportunities for analysis, entertainment and training.

Alpha–beta pruning is a search algorithm that seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player games. It stops evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.

An evaluation function, also known as a heuristic evaluation function or static evaluation function, is a function used by game-playing computer programs to estimate the value or goodness of a position in a game tree. A tree of such evaluations is usually part of a minimax or related search paradigm which returns a particular node and its evaluation as a result of alternately selecting the most favorable move for the side on move at each ply of the game tree. The value is a quantized scalar, often in nths of the value of a playing piece such as a stone in go or a pawn in chess. n may be tenths, hundredths or other convenient fraction.

In competitive two-player games, the killer heuristic is a technique for improving the efficiency of alpha-beta pruning, which in turn improves the efficiency of the minimax algorithm. This algorithm has an exponential search time to find the optimal next move, so general methods for speeding it up are very useful. Barbara Liskov created the general heuristic to speed tree search in a computer program to play chess endgames for her Ph.D. thesis.

In computer chess and other computer games, transposition tables are used to speed up the search of the game tree. Transposition tables are primarily useful in perfect-information games. The usage of transposition tables is essentially memoization applied to the tree search and is a form of dynamic programming.

The horizon effect, also known as the horizon problem, is a problem in artificial intelligence whereby, in many games, the number of possible states or positions is immense and computers can only feasibly search a small portion of them, typically a few plies down the game tree. Thus, for a computer searching only five plies, there is a possibility that it will make a detrimental move, but the effect is not visible because the computer does not search to the depth of the error.

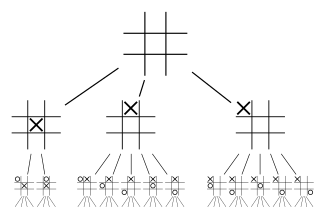
Game tree tree diagram used to find and analyze potential moves in a game

In game theory, a game tree is a directed graph whose nodes are positions in a game and whose edges are moves. The complete game tree for a game is the game tree starting at the initial position and containing all possible moves from each position; the complete tree is the same tree as that obtained from the extensive-form game representation.

Maven is an artificial intelligence Scrabble player, created by Brian Sheppard. It has been used in official licensed Hasbro Scrabble games.

The expectiminimax algorithm is a variation of the minimax algorithm, for use in artificial intelligence systems that play two-player zero-sum games, such as backgammon, in which the outcome depends on a combination of the player's skill and chance elements such as dice rolls. In addition to "min" and "max" nodes of the traditional minimax tree, this variant has "chance" nodes, which take the expected value of a random event occurring. In game theory terms, an expectiminimax tree is the game tree of an extensive-form game of perfect, but incomplete information.

Negamax search is a variant form of minimax search that relies on the zero-sum property of a two-player game.

Principal variation search is a negamax algorithm that can be faster than alpha-beta pruning. Like alpha-beta pruning, NegaScout is a directional search algorithm for computing the minimax value of a node in a tree. It dominates alpha-beta pruning in the sense that it will never examine a node that can be pruned by alpha-beta; however, it relies on accurate node ordering to capitalize on this advantage.

Quiescence search is an algorithm typically used to extend search at unstable nodes in minimax game trees in game-playing computer programs. It is an extension of the evaluation function to defer evaluation until the position is stable enough to be evaluated statically, that is, without considering the history of the position or future moves from the position. It mitigates the effect of the horizon problem faced by AI engines for various games like chess and Go.

Alexander Brudno Russian mathematician

Alexander L'vovich Brudno was a Russian computer scientist, best known for fully describing the alpha-beta pruning algorithm. From 1991 until his death he lived in Israel.

In computer chess, and in other games that computers play, late move reductions is a non-game specific enhancement to the alpha–beta algorithm and its variants which attempts to examine a game search tree more efficiently. It uses the assumption that good game-specific move ordering causes a program to search the most likely moves early. If a cut-off is going to happen in a search, the first few moves are the ones most likely to cause them. In games like chess, most programs search winning captures and "killers" first. Late move reductions will reduce the search depth for moves searched later at a given node. This allows the program to search deeper along the critical lines, and play better.

SSS* is a search algorithm, introduced by George Stockman in 1979, that conducts a state space search traversing a game tree in a best-first fashion similar to that of the A* search algorithm.

In computer science, B* is a best-first graph search algorithm that finds the least-cost path from a given initial node to any goal node. First published by Hans Berliner in 1979, it is related to the A* search algorithm.

In computer science, Monte Carlo tree search (MCTS) is a heuristic search algorithm for some kinds of decision processes, most notably those employed in game play. MCTS was introduced in 2006 for computer Go. It has been used in other board games like chess and shogi, games with incomplete information such as bridge and poker, as well as in real-time video games.

References

  1. ↑ Beal, Don F. (1990), "A generalised quiescence search algorithm", Artificial Intelligence, 43 (1): 85–98, doi:10.1016/0004-3702(90)90072-8 .
  2. ↑ Goetsch, G.; Campbell, M. S. (1990), "Experiments with the null-move heuristic", in Marsland, T. Anthony; Schaeffer, Jonathan (eds.), Computers, Chess, and Cognition, Springer-Verlag, pp. 159–168.


This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.