History
The numerical renormalization group is an inherently non-perturbative procedure, which was originally used to solve the Kondo model. [1] The Kondo model is a simplified theoretical model which describes a system of magnetic spin-1/2 impurities which couple to metallic conduction electrons (e.g. iron impurities in gold). This problem is notoriously difficult to tackle theoretically, since perturbative techniques break down at low-energy. However, Wilson was able to prove for the first time using the numerical renormalization group that the ground state of the Kondo model is a singlet state. But perhaps more importantly, the notions of renormalization, fixed points, and renormalization group flow were introduced to the field of condensed matter theory — it is for this that Wilson won the Nobel Prize in 1982. The complete behaviour of the Kondo model, including both the high-temperature 'local moment' regime and the low-temperature 'strong coupling' regime are captured by the numerical renormalization group; an exponentially small energy scale TK (not accessible from straight perturbation theory) was shown to govern all properties at low-energies, with all physical observables such as resistivity, thermodynamics, dynamics etc. exhibiting universal scaling. This is a characteristic feature of many problems in condensed matter physics, and is a central theme of quantum impurity physics in particular. In the original example of the Kondo model, the impurity local moment is completely screened below TK by the conduction electrons via the celebrated Kondo effect; and one famous consequence is that such materials exhibit a resistivity minimum at low temperatures, contrary to expectations based purely on the standard phonon contribution, where the resistivity is predicted to decrease monotonically with temperature.
The very existence of local moments in real systems of course presupposes strong electron-electron correlations. The Anderson impurity model describes a quantum level with an onsite Coulomb repulsion between electrons (rather than a spin), which is tunnel-coupled to metallic conduction electrons. In the singly occupied regime of the impurity, one can derive the Kondo model from the Anderson model, but the latter contains other physics associated with charge fluctuations. The numerical renormalization group was extended to deal with the Anderson model (capturing thereby both Kondo physics and valence fluctuation physics) by H. R. Krishnamurthy et al. [2] in 1980. Indeed, various important developments have been made since: a comprehensive modern review has been compiled by Bulla et al. [3]
Technique
The numerical renormalization group is an iterative procedure, which is an example of a renormalization group technique.
The technique consists of first dividing the conduction band into logarithmic intervals (i.e. intervals which get smaller exponentially as you move closer to the Fermi energy). One conduction band state from each interval is retained, this being the totally symmetric combination of all the states in that interval. The conduction band has now been "logarithmically discretized". The Hamiltonian is now in a position to be transformed into so-called linear chain form, in which the impurity is coupled to only one conduction band state, which is coupled to one other conduction band state and so on. Crucially, these couplings decrease exponentially along the chain, so that, even though the transformed Hamiltonian is for an infinite chain, one can consider a chain of finite length and still obtain useful results.
The only restriction to the conduction-band is that it is non-interacting. Recent developments [4] make it possible for mapping a general multi-channel conduction-band with channel mixing to a Wilson chain, and here is the python implementation.
Once the Hamiltonian is in linear chain form, one can begin the iterative process. First the isolated impurity is considered, which will have some characteristic set of energy levels. One then considers adding the first conduction band orbital to the chain. This causes a splitting in the energy levels for the isolated impurity. One then considers the effect of adding further orbitals along the chain, doing which splits the hitherto derived energy levels further. Because the couplings decrease along the chain, the successive splittings caused by adding orbitals to the chain decrease.
When a particular number of orbitals have been added to the chain, we have a set of energy levels for that finite chain. This is obviously not the true set of energy levels for the infinite chain, but it is a good approximation to the true set in the temperature range where: the further splittings caused by adding more orbitals is negligible, and we have enough orbitals in the chain to account for splittings which are relevant in this temperature range. The results of this is that the results derived for a chain of any particular length are valid only in a particular temperature range, a range which moves to lower temperatures as the chain length increases. This means that by considering the results at many different chain lengths, one can build up a picture of the behavior of the system over a wide temperature range.
The Hamiltonian for a linear chain of finite length is an example of an effective Hamiltonian. It is not the full Hamiltonian of the infinite linear chain system, but in a certain temperature range it gives similar results to the full Hamiltonian.
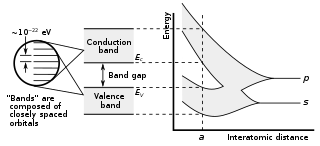
In solid-state physics, a band gap, also called an energy gap, is an energy range in a solid where no electronic states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the bottom of the conduction band in insulators and semiconductors. It is the energy required to promote a valence electron bound to an atom to become a conduction electron, which is free to move within the crystal lattice and serve as a charge carrier to conduct electric current. It is closely related to the HOMO/LUMO gap in chemistry. If the valence band is completely full and the conduction band is completely empty, then electrons cannot move within the solid because there are no available states. If the electrons are not free to move within the crystal lattice, then there is no generated current due to no net charge carrier mobility. However, if some electrons transfer from the valence band to the conduction band, then current can flow. Therefore, the band gap is a major factor determining the electrical conductivity of a solid. Substances with large band gaps are generally insulators, those with smaller band gaps are semiconductors, while conductors either have very small band gaps or none, because the valence and conduction bands overlap to form a continuous band.

Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian.
In theoretical physics, the term renormalization group (RG) refers to a formal apparatus that allows systematic investigation of the changes of a physical system as viewed at different scales. In particle physics, it reflects the changes in the underlying force laws as the energy scale at which physical processes occur varies, energy/momentum and resolution distance scales being effectively conjugate under the uncertainty principle.

In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities. Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Experiments in the 1960s by Myriam Sarachik at Bell Laboratories provided the first data that confirmed the Kondo effect. Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, and ytterbium, and actinide elements such as uranium. The Kondo effect has also been observed in quantum dot systems.

Kenneth Geddes "Ken" Wilson was an American theoretical physicist and a pioneer in leveraging computers for studying particle physics. He was awarded the 1982 Nobel Prize in Physics for his work on phase transitions—illuminating the subtle essence of phenomena like melting ice and emerging magnetism. It was embodied in his fundamental work on the renormalization group.

A polaron is a quasiparticle used in condensed matter physics to understand the interactions between electrons and atoms in a solid material. The polaron concept was proposed by Lev Landau in 1933 and Solomon Pekar in 1946 to describe an electron moving in a dielectric crystal where the atoms displace from their equilibrium positions to effectively screen the charge of an electron, known as a phonon cloud. This lowers the electron mobility and increases the electron's effective mass.

In physics, dephasing is a mechanism that recovers classical behaviour from a quantum system. It refers to the ways in which coherence caused by perturbation decays over time, and the system returns to the state before perturbation. It is an important effect in molecular and atomic spectroscopy, and in the condensed matter physics of mesoscopic devices.

The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard.

In particle physics, the history of quantum field theory starts with its creation by Paul Dirac, when he attempted to quantize the electromagnetic field in the late 1920s. Heisenberg was awarded the 1932 Nobel Prize in Physics "for the creation of quantum mechanics". Major advances in the theory were made in the 1940s and 1950s, leading to the introduction of renormalized quantum electrodynamics (QED). QED was so successful and accurately predictive that efforts were made to apply the same basic concepts for the other forces of nature. By the late 1970s, these efforts successfully utilized gauge theory in the strong nuclear force and weak nuclear force, producing the modern Standard Model of particle physics.
Quantum Monte Carlo encompasses a large family of computational methods whose common aim is the study of complex quantum systems. One of the major goals of these approaches is to provide a reliable solution of the quantum many-body problem. The diverse flavors of quantum Monte Carlo approaches all share the common use of the Monte Carlo method to handle the multi-dimensional integrals that arise in the different formulations of the many-body problem.
In physics, the Bethe ansatz is an ansatz method for finding the exact wavefunctions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian. Since then the method has been extended to other models in one dimension: the (anisotropic) Heisenberg chain, the Lieb-Liniger interacting Bose gas, the Hubbard model, the Kondo model, the Anderson impurity model, the Richardson model etc.
A charge density wave (CDW) is an ordered quantum fluid of electrons in a linear chain compound or layered crystal. The electrons within a CDW form a standing wave pattern and sometimes collectively carry an electric current. The electrons in such a CDW, like those in a superconductor, can flow through a linear chain compound en masse, in a highly correlated fashion. Unlike a superconductor, however, the electric CDW current often flows in a jerky fashion, much like water dripping from a faucet due to its electrostatic properties. In a CDW, the combined effects of pinning and electrostatic interactions likely play critical roles in the CDW current's jerky behavior, as discussed in sections 4 & 5 below.
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments. The name "heavy fermion" comes from the fact that the fermion behaves as if it has an effective mass greater than its rest mass. In the case of electrons, below a characteristic temperature (typically 10 K), the conduction electrons in these metallic compounds behave as if they had an effective mass up to 1000 times the free particle mass. This large effective mass is also reflected in a large contribution to the resistivity from electron-electron scattering via the Kadowaki–Woods ratio. Heavy fermion behavior has been found in a broad variety of states including metallic, superconducting, insulating and magnetic states. Characteristic examples are CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 and UPt3.
The Anderson impurity model, named after Philip Warren Anderson, is a Hamiltonian that is used to describe magnetic impurities embedded in metals. It is often applied to the description of Kondo effect-type problems, such as heavy fermion systems and Kondo insulators. In its simplest form, the model contains a term describing the kinetic energy of the conduction electrons, a two-level term with an on-site Coulomb repulsion that models the impurity energy levels, and a hybridization term that couples conduction and impurity orbitals. For a single impurity, the Hamiltonian takes the form
The timeline of quantum mechanics is a list of key events in the history of quantum mechanics, quantum field theories and quantum chemistry.
Dynamical mean-field theory (DMFT) is a method to determine the electronic structure of strongly correlated materials. In such materials, the approximation of independent electrons, which is used in density functional theory and usual band structure calculations, breaks down. Dynamical mean-field theory, a non-perturbative treatment of local interactions between electrons, bridges the gap between the nearly free electron gas limit and the atomic limit of condensed-matter physics.
The Rashba effect, also called Bychkov–Rashba effect, is a momentum-dependent splitting of spin bands in bulk crystals and low-dimensional condensed matter systems similar to the splitting of particles and anti-particles in the Dirac Hamiltonian. The splitting is a combined effect of spin–orbit interaction and asymmetry of the crystal potential, in particular in the direction perpendicular to the two-dimensional plane. This effect is named in honour of Emmanuel Rashba, who discovered it with Valentin I. Sheka in 1959 for three-dimensional systems and afterward with Yurii A. Bychkov in 1984 for two-dimensional systems.
The Kondo model is a model for a single localized quantum impurity coupled to a large reservoir of delocalized and noninteracting electrons. The quantum impurity is represented by a spin-1/2 particle, and is coupled to a continuous band of noninteracting electrons by an antiferromagnetic exchange coupling . The Kondo model is used as a model for metals containing magnetic impurities, as well as quantum dot systems.
Hulikal Ramaiengar Krishnamurthy is an Indian theoretical physicist. He specializes in theoretical condensed matter physics, especially quantum many-body theory and statistical physics. He was the chairman of the Department of Physics, Indian Institute of Science. His most well-known work is titled Renormalization Group Approach to the Anderson Model of Dilute Magnetic Alloys.
The Dresselhaus effect is a phenomenon in solid-state physics in which spin–orbit interaction causes energy bands to split. It is usually present in crystal systems lacking inversion symmetry. The effect is named after Gene Dresselhaus, husband of Mildred Dresselhaus, who discovered this splitting in 1955.






