
Quantum decoherence is the loss of quantum coherence, the process in which a system's behaviour changes from that which can be explained by quantum mechanics to that which can be explained by classical mechanics. In quantum mechanics, particles such as electrons are described by a wave function, a mathematical representation of the quantum state of a system; a probabilistic interpretation of the wave function is used to explain various quantum effects. As long as there exists a definite phase relation between different states, the system is said to be coherent. A definite phase relationship is necessary to perform quantum computing on quantum information encoded in quantum states. Coherence is preserved under the laws of quantum physics.
The Ising model, named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that represent magnetic dipole moments of atomic "spins" that can be in one of two states. The spins are arranged in a graph, usually a lattice, allowing each spin to interact with its neighbors. Neighboring spins that agree have a lower energy than those that disagree; the system tends to the lowest energy but heat disturbs this tendency, thus creating the possibility of different structural phases. The model allows the identification of phase transitions as a simplified model of reality. The two-dimensional square-lattice Ising model is one of the simplest statistical models to show a phase transition.

In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities. Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Experiments in the 1960s by Myriam Sarachik at Bell Laboratories provided the first data that confirmed the Kondo effect. Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, and ytterbium, and actinide elements such as uranium. The Kondo effect has also been observed in quantum dot systems.
In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

A Luttinger liquid, or Tomonaga–Luttinger liquid, is a theoretical model describing interacting electrons in a one-dimensional conductor. Such a model is necessary as the commonly used Fermi liquid model breaks down for one dimension.

The Hubbard model is an approximate model used to describe the transition between conducting and insulating systems. It is particularly useful in solid-state physics. The model is named for John Hubbard.

In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.
In solid-state physics, heavy fermion materials are a specific type of intermetallic compound, containing elements with 4f or 5f electrons in unfilled electron bands. Electrons are one type of fermion, and when they are found in such materials, they are sometimes referred to as heavy electrons. Heavy fermion materials have a low-temperature specific heat whose linear term is up to 1000 times larger than the value expected from the free electron model. The properties of the heavy fermion compounds often derive from the partly filled f-orbitals of rare-earth or actinide ions, which behave like localized magnetic moments. The name "heavy fermion" comes from the fact that the fermion behaves as if it has an effective mass greater than its rest mass. In the case of electrons, below a characteristic temperature (typically 10 K), the conduction electrons in these metallic compounds behave as if they had an effective mass up to 1000 times the free particle mass. This large effective mass is also reflected in a large contribution to the resistivity from electron-electron scattering via the Kadowaki–Woods ratio. Heavy fermion behavior has been found in a broad variety of states including metallic, superconducting, insulating and magnetic states. Characteristic examples are CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 and UPt3.
A schema is a template in computer science used in the field of genetic algorithms that identifies a subset of strings with similarities at certain string positions. Schemata are a special case of cylinder sets, forming a basis for a product topology on strings. In other words, schemata can be used to generate a topology on a space of strings.
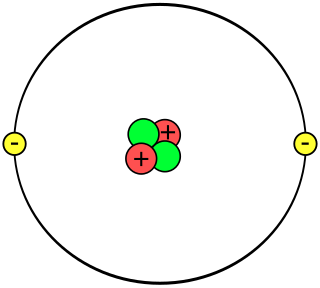
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom.
The Stoner criterion is a condition to be fulfilled for the ferromagnetic order to arise in a simplified model of a solid. It is named after Edmund Clifton Stoner.
A flavor of the k·p perturbation theory used for calculating the structure of multiple, degenerate electronic bands in bulk and quantum well semiconductors. The method is a generalization of the single band k·p theory.
In solid mechanics, the Johnson–Holmquist damage model is used to model the mechanical behavior of damaged brittle materials, such as ceramics, rocks, and concrete, over a range of strain rates. Such materials usually have high compressive strength but low tensile strength and tend to exhibit progressive damage under load due to the growth of microfractures.
Dynamical mean-field theory (DMFT) is a method to determine the electronic structure of strongly correlated materials. In such materials, the approximation of independent electrons, which is used in density functional theory and usual band structure calculations, breaks down. Dynamical mean-field theory, a non-perturbative treatment of local interactions between electrons, bridges the gap between the nearly free electron gas limit and the atomic limit of condensed-matter physics.
The Rashba effect, also called Bychkov–Rashba effect, is a momentum-dependent splitting of spin bands in bulk crystals and low-dimensional condensed matter systems similar to the splitting of particles and anti-particles in the Dirac Hamiltonian. The splitting is a combined effect of spin–orbit interaction and asymmetry of the crystal potential, in particular in the direction perpendicular to the two-dimensional plane. This effect is named in honour of Emmanuel Rashba, who discovered it with Valentin I. Sheka in 1959 for three-dimensional systems and afterward with Yurii A. Bychkov in 1984 for two-dimensional systems.
The Kondo model is a model for a single localized quantum impurity coupled to a large reservoir of delocalized and noninteracting electrons. The quantum impurity is represented by a spin-1/2 particle, and is coupled to a continuous band of noninteracting electrons by an antiferromagnetic exchange coupling . The Kondo model is used as a model for metals containing magnetic impurities, as well as quantum dot systems.
In condensed matter physics, the resonating valence bond theory (RVB) is a theoretical model that attempts to describe high-temperature superconductivity, and in particular the superconductivity in cuprate compounds. It was first proposed by an American physicist P. W. Anderson and Indian theoretical physicist Ganapathy Baskaran in 1987. The theory states that in copper oxide lattices, electrons from neighboring copper atoms interact to form a valence bond, which locks them in place. However, with doping, these electrons can act as mobile Cooper pairs and are able to superconduct. Anderson observed in his 1987 paper that the origins of superconductivity in doped cuprates was in the Mott insulator nature of crystalline copper oxide. RVB builds on the Hubbard and t-J models used in the study of strongly correlated materials.
In computational solid state physics, Continuous-time quantum Monte Carlo (CT-QMC) is a family of stochastic algorithms for solving the Anderson impurity model at finite temperature. These methods first expand the full partition function as a series of Feynman diagrams, employ Wick's theorem to group diagrams into determinants, and finally use Markov chain Monte Carlo to stochastically sum up the resulting series.
The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are Graphene, topological insulators, Dirac semimetals, Weyl semimetals, various high-temperature superconductors with -wave pairing and liquid Helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the Dirac matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.
The transverse field Ising model is a quantum version of the classical Ising model. It features a lattice with nearest neighbour interactions determined by the alignment or anti-alignment of spin projections along the axis, as well as an external magnetic field perpendicular to the axis which creates an energetic bias for one x-axis spin direction over the other.


























