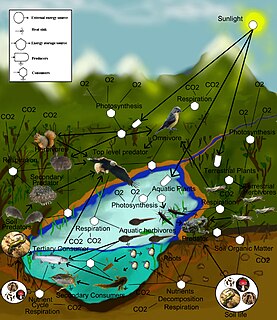
Theoretical ecology is the scientific discipline devoted to the study of ecological systems using theoretical methods such as simple conceptual models, mathematical models, computational simulations, and advanced data analysis. Effective models improve understanding of the natural world by revealing how the dynamics of species populations are often based on fundamental biological conditions and processes. Further, the field aims to unify a diverse range of empirical observations by assuming that common, mechanistic processes generate observable phenomena across species and ecological environments. Based on biologically realistic assumptions, theoretical ecologists are able to uncover novel, non-intuitive insights about natural processes. Theoretical results are often verified by empirical and observational studies, revealing the power of theoretical methods in both predicting and understanding the noisy, diverse biological world.

Predation is a biological interaction where one organism, the predator, kills and eats another organism, its prey. It is one of a family of common feeding behaviours that includes parasitism and micropredation and parasitoidism. It is distinct from scavenging on dead prey, though many predators also scavenge; it overlaps with herbivory, as seed predators and destructive frugivores are predators.

Parasteatoda tepidariorum, the common house spider, referred to internationally as the American house spider, is a spider species of the genus Parasteatoda that is mainly indigenous to the New World, with P. tepidariorum australis but has achieved a cosmopolitan distribution. American house spiders are synanthropic and build their tangled webs in or near human dwellings, greenhouses or similar, often in secluded areas such as between loose walls and behind open doors and attic windows. Statistically, they are the most often encountered spider by humans in North America, and least likely to adopt defensive behavior in their vicinity. Their prey mechanism is similar to that of the other cobweb spiders: the spider follows disturbances transmitted along the web to entangle and then paralyze its prey, which usually consists of household insects and other invertebrates.

The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order nonlinear differential equations, frequently used to describe the dynamics of biological systems in which two species interact, one as a predator and the other as prey. The populations change through time according to the pair of equations:
Population dynamics is the type of mathematics used to model and study the size and age composition of populations as dynamical systems.

Population ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment, such as birth and death rates, and by immigration and emigration).

A metapopulation consists of a group of spatially separated populations of the same species which interact at some level. The term metapopulation was coined by Richard Levins in 1969 to describe a model of population dynamics of insect pests in agricultural fields, but the idea has been most broadly applied to species in naturally or artificially fragmented habitats. In Levins' own words, it consists of "a population of populations".

Optimal foraging theory (OFT) is a behavioral ecology model that helps predict how an animal behaves when searching for food. Although obtaining food provides the animal with energy, searching for and capturing the food require both energy and time. To maximize fitness, an animal adopts a foraging strategy that provides the most benefit (energy) for the lowest cost, maximizing the net energy gained. OFT helps predict the best strategy that an animal can use to achieve this goal.
MIMIC, known in capitalized form only, is a former simulation computer language developed 1964 by H. E. Petersen, F. J. Sansom and L. M. Warshawsky of Systems Engineering Group within the Air Force Materiel Command at the Wright-Patterson AFB in Dayton, Ohio, United States. It is an expression-oriented continuous block simulation language, but capable of incorporating blocks of FORTRAN-like algebra.
The paradox of enrichment is a term from population ecology coined by Michael Rosenzweig in 1971. He described an effect in six predator–prey models where increasing the food available to the prey caused the predator's population to destabilize. A common example is that if the food supply of a prey such as a rabbit is overabundant, its population will grow unbounded and cause the predator population to grow unsustainably large. That may result in a crash in the population of the predators and possibly lead to local eradication or even species extinction.

A functional response in ecology is the intake rate of a consumer as a function of food density. It is associated with the numerical response, which is the reproduction rate of a consumer as a function of food density. Following C. S. Holling, functional responses are generally classified into three types, which are called Holling's type I, II, and III.

An ecosystem model is an abstract, usually mathematical, representation of an ecological system, which is studied to better understand the real system.
A population model is a type of mathematical model that is applied to the study of population dynamics.
The Nicholson–Bailey model was developed in the 1930s to describe the population dynamics of a coupled host-parasitoid system. It is named after Alexander John Nicholson and Victor Albert Bailey. Host-parasite and prey-predator systems can also be represented with the Nicholson-Bailey model. The model is closely related to the Lotka–Volterra model, which describes the dynamics of antagonistic populations using differential equations.

A fishery is an area with an associated fish or aquatic population which is harvested for its commercial or recreational value. Fisheries can be wild or farmed. Population dynamics describes the ways in which a given population grows and shrinks over time, as controlled by birth, death, and migration. It is the basis for understanding changing fishery patterns and issues such as habitat destruction, predation and optimal harvesting rates. The population dynamics of fisheries is used by fisheries scientists to determine sustainable yields.
The paradox of the pesticides is a paradox that states that applying pesticide to a pest may end up increasing the abundance of the pest if the pesticide upsets natural predator–prey dynamics in the ecosystem.
The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator–prey examples of Lotka–Volterra types. They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their dynamics can be analysed analytically to some extent. This makes them useful as a theoretical tool for modeling food webs. However, they lack features of other ecological models such as predator preference and nonlinear functional responses, and they cannot be used to model mutualism without allowing indefinite population growth.

Lev R. Ginzburg is a mathematical ecologist and the President of the firm Applied Biomathematics.
The Arditi–Ginzburg equations describes ratio dependent predator–prey dynamics. Where N is the population of a prey species and P that of a predator, the population dynamics are described by the following two equations:

Pursuit predation is a form of predation in which predators give chase to fleeing prey. The chase can be initiated either by the predator or by the prey, should the prey be alerted to a predator's presence and attempt to flee before the predator gives chase. The chase ends when either the predator captures and consumes the prey, or the prey escapes. Pursuit predation is typically observed in carnivorous species within the kingdom Animalia, with some iconic examples being cheetahs, lions, and wolves.












