Related Research Articles
In computer science, an online algorithm is one that can process its input piece-by-piece in a serial fashion, i.e., in the order that the input is fed to the algorithm, without having the entire input available from the start.

The travelling salesman problem asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

Linear programming is a method to achieve the best outcome in a mathematical model whose requirements are represented by linear relationships. Linear programming is a special case of mathematical programming.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.

A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
The Bottleneck traveling salesman problem is a problem in discrete or combinatorial optimization. The problem is to find the Hamiltonian cycle in a weighted graph which minimizes the weight of the highest-weight edge of the cycle. It was first formulated by Gilmore & Gomory (1964) with some additional constraints, and in its full generality by Garfinkel & Gilbert (1978).

Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there are also many approximation algorithms that provide an additive guarantee on the quality of the returned solution. A notable example of an approximation algorithm that provides both is the classic approximation algorithm of Lenstra, Shmoys and Tardos for scheduling on unrelated parallel machines.
In mathematics, computer science and economics, an optimization problem is the problem of finding the best solution from all feasible solutions.
In computational complexity theory, the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant. In simple terms, problems in this class have efficient algorithms that can find an answer within some fixed multiplicative factor of the optimal answer.
In computer science, graph traversal refers to the process of visiting each vertex in a graph. Such traversals are classified by the order in which the vertices are visited. Tree traversal is a special case of graph traversal.
Competitive analysis is a method invented for analyzing online algorithms, in which the performance of an online algorithm is compared to the performance of an optimal offline algorithm that can view the sequence of requests in advance. An algorithm is competitive if its competitive ratio—the ratio between its performance and the offline algorithm's performance—is bounded. Unlike traditional worst-case analysis, where the performance of an algorithm is measured only for "hard" inputs, competitive analysis requires that an algorithm perform well both on hard and easy inputs, where "hard" and "easy" are defined by the performance of the optimal offline algorithm.
As applied in the field of computer vision, graph cut optimization can be employed to efficiently solve a wide variety of low-level computer vision problems, such as image smoothing, the stereo correspondence problem, image segmentation, object co-segmentation, and many other computer vision problems that can be formulated in terms of energy minimization. Many of these energy minimization problems can be approximated by solving a maximum flow problem in a graph. Under most formulations of such problems in computer vision, the minimum energy solution corresponds to the maximum a posteriori estimate of a solution. Although many computer vision algorithms involve cutting a graph, the term "graph cuts" is applied specifically to those models which employ a max-flow/min-cut optimization.
In computer science, the ski rental problem is a name given to a class of problems in which there is a choice between continuing to pay a repeating cost or paying a one-time cost which eliminates or reduces the repeating cost.
In computer science and graph theory, the Canadian traveller problem (CTP) is a generalization of the shortest path problem to graphs that are partially observable. In other words, the graph is revealed while it is being explored, and explorative edges are charged even if they do not contribute to the final path.
Clustering is the problem of partitioning data points into groups based on their similarity. Correlation clustering provides a method for clustering a set of objects into the optimum number of clusters without specifying that number in advance.
In computational complexity theory, a gap reduction is a reduction to a particular type of decision problem, known as a c-gap problem. Such reductions provide information about the hardness of approximating solutions to optimization problems. In short, a gap problem refers to one wherein the objective is to distinguish between cases where the best solution is above one threshold from cases where the best solution is below another threshold, such that the two thresholds have a gap in between. Gap reductions can be used to demonstrate inapproximability results, as if a problem may be approximated to a better factor than the size of gap, then the approximation algorithm can be used to solve the corresponding gap problem.
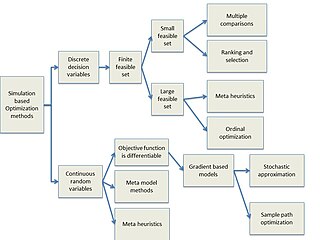
Simulation-based optimization integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that the objective function must be estimated using statistical estimation techniques.
The vertex k-center problem is a classical NP-hard problem in computer science. It has application in facility location and clustering. Basically, the vertex k-center problem models the following real problem: given a city with facilities, find the best facilities where to build fire stations. Since firemen must attend any emergency as quickly as possible, the distance from the farthest facility to its nearest fire station has to be as small as possible. In other words, the position of the fire stations must be such that every possible fire is attended as quickly as possible.
References
- ↑ Jaillet, Patrick, and Michael R. Wagner. Online Optimization. Springer Publishing Company, Incorporated, 2012.
- ↑ Dochow, Robert (2016). Online Algorithms for the Portfolio Selection Problem. Springer Gabler.