Ski rental problem

Last updated October 08, 2024

In computer science, the ski rental problem is a name given to a class of problems in which there is a choice between continuing to pay a repeating cost or paying a one-time cost which eliminates or reduces the repeating cost.^[1]

The problem

Many online problems have a sub-problem called the rent-or-buy problem. Given an expensive up front cost, or a less expensive repeating cost, with no knowledge of how the future will play out, at what point is it better to pay the up front cost to avoid a continued repeating cost?

Consider a person who decides to go skiing, but for an undecided number of days. Renting skis costs $1 per day, whereas buying a pair of skis costs $10. If the person knows in advance how many days they want to ski, then the breakeven point is 10 days. Fewer than 10 days, renting is preferable, whereas with more than 10 days, buying is preferable. However, with no advance knowledge of how long one will be skiing, the breakeven point is unclear. A good algorithm will minimize the ratio of the cost when the number of days is known in advance to the cost when the number of days is not known in advance.^[2] Ski rental^[3]^[4] is one example of this class of problem.

The break-even algorithm

The break-even algorithm instructs one to rent for 9 days and buy skis on the morning of day 10 if one is still up for skiing.^[5] If one has to stop skiing during the first 9 days, it costs the same as what one would pay if one had known the number of days one would go skiing. If one has to stop skiing after day 10, one's cost is $19 which is 90% more than what one would pay if one had known the number of days one would go skiing in advance. This is the worst case for the break-even algorithm.

The break-even algorithm is known to be the best deterministic algorithm for this problem.

The randomized algorithm

A person can flip a coin. If it comes up heads, she buys skis on day eight; otherwise, she buys skis on day 10. This is an instance of a randomized algorithm. The expected cost is at most 80% more than what the person would pay if she had known the number of days she would go skiing, regardless of how many days she skis. In particular, if the person skis for 10 days, her expected cost is 1/2 [7 +10] + 1/2 [9+10] = 18 dollars, only 80% excess instead of 90%.

A randomized algorithm can be understood as a composition of different algorithms, each one which occurs with a given probability. We define the expected competitive ratio on a given instance i as:

$E_{i}=\sum _{j}P(ALG_{j})\cdot ALG_{j}(i)$ , where $ALG_{j}(i)$ is the competitive ratio for instance i, given $ALG_{j}$ .

Consequently, the competitive ratio of a randomized algorithm is given by the worst value of $E_{i}$ over all given instances. In the case of the coin flipping ski-rental, we note that the randomized algorithm has 2 possible branches: If the coin comes up heads, we buy on day 8, otherwise we buy on day 10. We may call the branches $ALG_{heads}$ and $ALG_{tails}$ , respectively. $E_{i}=P(ALG_{heads})\cdot ALG_{heads}(i)+P(ALG_{tails})\cdot ALG_{tails}(i)={\frac {1}{2}}\cdot 1+{\frac {1}{2}}\cdot 1=1$ , for $i<8$ .

$E_{8}=P(ALG_{heads})\cdot ALG_{heads}(8)+P(ALG_{tails})\cdot ALG_{tails}(8)={\frac {1}{2}}\cdot {\frac {17}{8}}+{\frac {1}{2}}\cdot 1=1.5625$ ,

$E_{9}=P(ALG_{heads})\cdot ALG_{heads}(9)+P(ALG_{tails})\cdot ALG_{tails}(9)={\frac {1}{2}}\cdot {\frac {17}{9}}+{\frac {1}{2}}\cdot 1=1.444444$ , and

$E_{i}=P(ALG_{heads})\cdot ALG_{heads}(i)+P(ALG_{tails})\cdot ALG_{tails}(i)={\frac {1}{2}}\cdot {\frac {17}{10}}+{\frac {1}{2}}\cdot {\frac {19}{10}}=1.8$ , for $i\geq 10$ .

Therefore, the competitive ratio of the randomized ski-rental coin flipping algorithm is 1.8.

The best randomized algorithm against an oblivious adversary is to choose some day i at random according to the following distribution p, rent for i-1 days and buy skis on the morning of day i if one are still up for skiing. Karlin et al.^[3] first presented this algorithm with distribution $p_{i}=\left\{{\begin{array}{ll}({\frac {b-1}{b}})^{b-i}{\frac {1}{b(1-(1-(1/b))^{b})}}&i\leq b\\0&i>b\end{array}}\right.,$ where buying skis costs $ $b$ and renting costs $1. Its expected cost is at most e/(e-1) $\approx$ 1.58 times what one would pay if one had known the number of days one would go skiing. No randomized algorithm can do better.

Applications

Snoopy caching:^[3] several caches share the same memory space that is partitioned into blocks. When a cache writes to a block, caches that share the block spend 1 bus cycle to get updated. These caches can invalidate the block to avoid the cost of updating. But there is a penalty of p bus cycles for invalidating a block from a cache that shortly thereafter needs access to it. We can break the write request sequences for several caches into request sequences for two caches. One cache performs a sequence of write operations to the block. The other cache needs to decide whether to get updated by paying 1 bus cycle per operation or invalidate the block by paying p bus cycles for future read request of itself. The two cache, one block snoopy caching problem is just the ski rental problem.

TCP acknowledgment:^[6] A stream of packets arrive at a destination and are required by the TCP protocol to be acknowledged upon arrival. However, we can use a single acknowledgment packet to simultaneously acknowledge multiple outstanding packets, thereby reducing the overhead of the acknowledgments. On the other hand, delaying acknowledgments too much can interfere with the TCP's congestion control mechanisms, and thus we should not allow the latency between a packet's arrival time and the time at which the acknowledgment is sent to increase too much. Karlin et al.^[7] described a one-parameter family of inputs, called the basis inputs, and showed that when restricted to these basis inputs, the TCP acknowledgement problem behaves the same as the ski rental problem.

Total completion time scheduling:^[2] We wish to schedule jobs with fixed processing times on m identical machines. The processing time of job j is p_j. Each job becomes known to the scheduler on its release time r_j. The goal is to minimize the sum of completion times over all jobs. A simplified problem is one single machine with the following input: at time 0, a job with processing time 1 arrives; k jobs with processing time 0 arrive at some unknown time. We need to choose a start time for the first job. Waiting incurs a cost of 1 per time unit, yet starting the first job before the later k jobs may incur an extra cost of k in the worst case. This simplified problem may be viewed as a continuous version of the ski rental problem.

Refactoring versus working with a poor design: In software development, engineers have to choose between the friction and risk of errors of working with an overly-complex design and reducing the complexity of the design before making a change. The extra cost of each change with the old design is the "rental" cost, the cost of refactoring is the "buy" cost. "How many times does one work with a poor design before cleaning it up?" is a ski rental problem.

Related Research Articles

In mathematics and computer programming, exponentiating by squaring is a general method for fast computation of large positive integer powers of a number, or more generally of an element of a semigroup, like a polynomial or a square matrix. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. These can be of quite general use, for example in modular arithmetic or powering of matrices. For semigroups for which additive notation is commonly used, like elliptic curves used in cryptography, this method is also referred to as double-and-add.

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesX_i are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable X_i in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.

In probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli, is the discrete probability distribution of a random variable which takes the value 1 with probability $and the value 0 with probability . Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes-no question. Such questions lead to outcomes that are Boolean-valued: a single bit whose value is success/yes/true/one with probability p and failure/no/false/zero with probability q . It can be used to represent a coin toss where 1 and 0 would represent "heads" and "tails", respectively, and p would be the probability of the coin landing on heads. In particular, unfair coins would have$

The bin packing problem is an optimization problem, in which items of different sizes must be packed into a finite number of bins or containers, each of a fixed given capacity, in a way that minimizes the number of bins used. The problem has many applications, such as filling up containers, loading trucks with weight capacity constraints, creating file backups in media, splitting a network prefix into multiple subnets, and technology mapping in FPGA semiconductor chip design.

In numerical analysis and computational statistics, rejection sampling is a basic technique used to generate observations from a distribution. It is also commonly called the acceptance-rejection method or "accept-reject algorithm" and is a type of exact simulation method. The method works for any distribution in $with a density.$

In electrical engineering, statistical computing and bioinformatics, the Baum–Welch algorithm is a special case of the expectation–maximization algorithm used to find the unknown parameters of a hidden Markov model (HMM). It makes use of the forward-backward algorithm to compute the statistics for the expectation step.

In machine learning, backpropagation is a gradient estimation method commonly used for training neural networks to compute the network parameter updates.

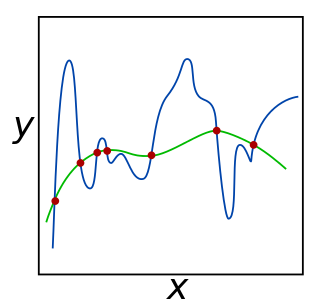
<span class="mw-page-title-main">Regularization (mathematics)</span> Technique to make a model more generalizable and transferable

In mathematics, statistics, finance, and computer science, particularly in machine learning and inverse problems, regularization is a process that converts the answer of a problem to a simpler one. It is often used in solving ill-posed problems or to prevent overfitting.

In probability theory, if a large number of events are all independent of one another and each has probability less than 1, then there is a positive probability that none of the events will occur. The Lovász local lemma allows one to relax the independence condition slightly: As long as the events are "mostly" independent from one another and aren't individually too likely, then there will still be a positive probability that none of them occurs. It is most commonly used in the probabilistic method, in particular to give existence proofs.

The cross-entropy (CE) method is a Monte Carlo method for importance sampling and optimization. It is applicable to both combinatorial and continuous problems, with either a static or noisy objective.

TCP-Illinois is a variant of TCP congestion control protocol, developed at the University of Illinois at Urbana–Champaign. It is especially targeted at high-speed, long-distance networks. A sender side modification to the standard TCP congestion control algorithm, it achieves a higher average throughput than the standard TCP, allocates the network resource fairly as the standard TCP, is compatible with the standard TCP, and provides incentives for TCP users to switch.

Stochastic approximation methods are a family of iterative methods typically used for root-finding problems or for optimization problems. The recursive update rules of stochastic approximation methods can be used, among other things, for solving linear systems when the collected data is corrupted by noise, or for approximating extreme values of functions which cannot be computed directly, but only estimated via noisy observations.

In computer science and graph theory, Karger's algorithm is a randomized algorithm to compute a minimum cut of a connected graph. It was invented by David Karger and first published in 1993.

The Price of Anarchy (PoA) is a concept in economics and game theory that measures how the efficiency of a system degrades due to selfish behavior of its agents. It is a general notion that can be extended to diverse systems and notions of efficiency. For example, consider the system of transportation of a city and many agents trying to go from some initial location to a destination. Here, efficiency means the average time for an agent to reach the destination. In the 'centralized' solution, a central authority can tell each agent which path to take in order to minimize the average travel time. In the 'decentralized' version, each agent chooses its own path. The Price of Anarchy measures the ratio between average travel time in the two cases.

Within theoretical computer science, the Sun–Ni law is a memory-bounded speedup model which states that as computing power increases the corresponding increase in problem size is constrained by the system’s memory capacity. In general, as a system grows in computational power, the problems run on the system increase in size. Analogous to Amdahl's law, which says that the problem size remains constant as system sizes grow, and Gustafson's law, which proposes that the problem size should scale but be bound by a fixed amount of time, the Sun–Ni law states the problem size should scale but be bound by the memory capacity of the system. Sun–Ni law was initially proposed by Xian-He Sun and Lionel Ni at the Proceedings of IEEE Supercomputing Conference 1990.

MAXEkSAT is a problem in computational complexity theory that is a maximization version of the Boolean satisfiability problem 3SAT. In MAXEkSAT, each clause has exactly k literals, each with distinct variables, and is in conjunctive normal form. These are called k-CNF formulas. The problem is to determine the maximum number of clauses that can be satisfied by a truth assignment to the variables in the clauses.

The maximum coverage problem is a classical question in computer science, computational complexity theory, and operations research. It is a problem that is widely taught in approximation algorithms.

The List Update or the List Access problem is a simple model used in the study of competitive analysis of online algorithms. Given a set of items in a list where the cost of accessing an item is proportional to its distance from the head of the list, e.g. a linked List, and a request sequence of accesses, the problem is to come up with a strategy of reordering the list so that the total cost of accesses is minimized. The reordering can be done at any time but incurs a cost. The standard model includes two reordering actions:

In PAC learning, error tolerance refers to the ability of an algorithm to learn when the examples received have been corrupted in some way. In fact, this is a very common and important issue since in many applications it is not possible to access noise-free data. Noise can interfere with the learning process at different levels: the algorithm may receive data that have been occasionally mislabeled, or the inputs may have some false information, or the classification of the examples may have been maliciously adulterated.

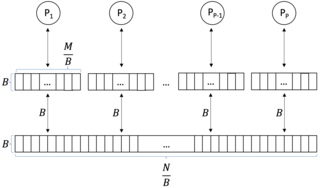
In computer science, a parallel external memory (PEM) model is a cache-aware, external-memory abstract machine. It is the parallel-computing analogy to the single-processor external memory (EM) model. In a similar way, it is the cache-aware analogy to the parallel random-access machine (PRAM). The PEM model consists of a number of processors, together with their respective private caches and a shared main memory.

References

↑ Blum, Avrim. "cos 521: Advanced Algorithm Design Lecture 24: Online Algorithms" (PDF). Computer Science Princeton University. Princeton University. Retrieved 2022-07-16.
1 2 Steven S. Seiden. A guessing game and randomized online algorithms. Annual ACM Symposium on Theory of Computing, 2000. http://portal.acm.org/citation.cfm?id=335385
1 2 3 A. R. Karlin, M. S. Manasse, L. A. McGeoch, and S. Owicki. Competitive randomized algorithms for non-uniform problems. In Proceedings of the First Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, 22–24 January 1990, pp. 301-309. Also in Algorithmica, 11(6): 542-571, 1994. http://courses.csail.mit.edu/6.895/fall03/handouts/papers/karlin.pdf
↑ Claire Mathieu. Brown University. Lecture note: http://www.cs.brown.edu/~claire/Talks/skirental.pdf
↑ A. R. Karlin, M. Manasse, L. Rudolph and D. Sleator. Competitive snoopy caching. Algorithmica, 3(1): 79-119, 1988
↑ Dooly, Daniel R.; Goldman, Sally A.; Scott, Stephen D. (1998). "TCP Dynamic Acknowledgment Delay: Theory and Practice (Extended Abstract)". In Vitter, Jeffrey Scott (ed.). Proceedings of the Thirtieth Annual ACM Symposium on the Theory of Computing, Dallas, Texas, USA, May 23-26, 1998. {ACM}. pp. 389–398. doi: 10.1145/276698.276792 .
↑ Anna R. Karlin and Claire Kenyon and Dana Randall. Dynamic TCP acknowledgement and other stories about e/(e-1). Thirty-Third Annual ACM Symposium on Theory of Computing (STOC), 2001. Algorithmica. http://www.cs.brown.edu/people/claire/Publis/ACKpaper.ps

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Blum, Avrim. "cos 521: Advanced Algorithm Design Lecture 24: Online Algorithms" (PDF). Computer Science Princeton University. Princeton University. Retrieved 2022-07-16.

[seiden-2] 1 2 Steven S. Seiden. A guessing game and randomized online algorithms. Annual ACM Symposium on Theory of Computing, 2000. http://portal.acm.org/citation.cfm?id=335385

[Karlin1994-3] 1 2 3 A. R. Karlin, M. S. Manasse, L. A. McGeoch, and S. Owicki. Competitive randomized algorithms for non-uniform problems. In Proceedings of the First Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, 22–24 January 1990, pp. 301-309. Also in Algorithmica, 11(6): 542-571, 1994. http://courses.csail.mit.edu/6.895/fall03/handouts/papers/karlin.pdf

[4] Claire Mathieu. Brown University. Lecture note: http://www.cs.brown.edu/~claire/Talks/skirental.pdf

[Karlin1988-5] A. R. Karlin, M. Manasse, L. Rudolph and D. Sleator. Competitive snoopy caching. Algorithmica, 3(1): 79-119, 1988

[6] Dooly, Daniel R.; Goldman, Sally A.; Scott, Stephen D. (1998). "TCP Dynamic Acknowledgment Delay: Theory and Practice (Extended Abstract)". In Vitter, Jeffrey Scott (ed.). Proceedings of the Thirtieth Annual ACM Symposium on the Theory of Computing, Dallas, Texas, USA, May 23-26, 1998. {ACM}. pp. 389–398. doi: 10.1145/276698.276792 .

[7] Anna R. Karlin and Claire Kenyon and Dana Randall. Dynamic TCP acknowledgement and other stories about e/(e-1). Thirty-Third Annual ACM Symposium on Theory of Computing (STOC), 2001. Algorithmica. http://www.cs.brown.edu/people/claire/Publis/ACKpaper.ps

[1]

[2]

[3]

[4]

[5]

[6]

[7]