Optical cluster state

Optical cluster states are a proposed tool to achieve quantum computational universality in linear optical quantum computing (LOQC). ^[1] As direct entangling operations with photons often require nonlinear effects, probabilistic generation of entangled resource states has been proposed as an alternative path to the direct approach.

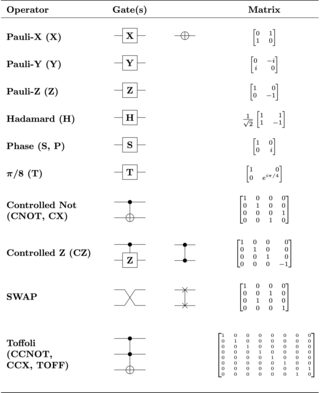
Creation of the cluster state

On a silicon photonic chip, one of the most common platforms for implementing LOQC, there are two typical choices for encoding quantum information, though many more options exist. ^[2] Photons have useful degrees of freedom in the spatial modes of the possible photon paths or in the polarization of the photons themselves. The way in which a cluster state is generated varies with which encoding has been chosen for implementation.

Storing information in the spatial modes of the photon paths is often referred to as dual rail encoding. In a simple case, one might consider the situation where a photon has two possible paths, a horizontal path with creation operator ${\displaystyle a^{\dagger }}$ and a vertical path with creation operator ${\displaystyle b^{\dagger }}$, where the logical zero and one states are then represented by

${\displaystyle a^{\dagger }|0_{a},0_{b}\rangle =|1_{a},0_{b}\rangle =|0\rangle _{L}}$

and

${\displaystyle b^{\dagger }|0_{a},0_{b}\rangle =|0_{a},1_{b}\rangle =|1\rangle _{L}}$.

Single qubit operations are then performed by beam splitters, which allow manipulation of the relative superposition weights of the modes, and phase shifters, which allow manipulation of the relative phases of the two modes. This type of encoding lends itself to the Nielsen protocol for generating cluster states. In encoding with photon polarization, logical zero and one can be encoded via the horizontal and vertical states of a photon, e.g.

${\displaystyle |H\rangle =|0\rangle _{L}}$

and

${\displaystyle |V\rangle =|1\rangle _{L}}$.

Given this encoding, single qubit operations can be performed using waveplates. This encoding can be used with the Browne-Rudolph protocol.

Nielsen protocol

In 2004, Nielsen proposed a protocol to create cluster states, ^[3] borrowing techniques from the Knill-Laflamme-Milburn protocol (KLM protocol) to probabilistically create controlled-Z connections between qubits which, when performed on a pair of ${\displaystyle |+\rangle =|0\rangle +|1\rangle }$ states (normalization being ignored), forms the basis for cluster states. While the KLM protocol requires error correction and a fairly large number of modes in order to get very high probability two-qubit gate, Nielsen's protocol only requires a success probability per gate of greater than one half. Given that the success probability for a connection using ${\displaystyle n}$ ancilla photons is ${\displaystyle n^{2}/(n+1)^{2}}$, relaxation of the success probability from nearly one to anything over one half presents a major advantage in resources, as well as simply reducing the number of required elements in the photonic circuit.

To see how Nielsen brought about this improvement, consider the photons being generated for qubits as vertices on a two dimensional grid, and the controlled-Z operations being probabilistically added edges between nearest neighbors. Using results from percolation theory, it can be shown that as long as the probability of adding edges is above a certain threshold, there will exist a complete grid as a sub-graph with near unit probability. Because of this, Nielsen's protocol doesn't rely on every individual connection being successful, just enough of them that the connections between photons allow a grid.

Yoran-Reznik protocol

Among the first proposals of utilizing resource states for optical quantum computing was the Yoran-Reznik protocol in 2003. ^[4] While the proposed resource in this protocol was not exactly a cluster state, it brought many of the same key concepts to the attention of those considering the possibilities of optical quantum computing and still required connecting multiple separate one-dimensional chains of entangled photons via controlled-Z operations. This protocol is somewhat unique in that it utilizes both the spatial mode degree of freedom along with the polarization degree of freedom to help entanglement between qubits.

Given a horizontal path, denoted by ${\displaystyle a}$, and a vertical path, denoted by ${\displaystyle b}$, a 50:50 beam splitter connecting the paths followed by a ${\displaystyle \pi /2}$-phase shifter on path ${\displaystyle a}$, we can perform the transformations

${\displaystyle |H,a\rangle \rightarrow {\frac {1}{\sqrt {2}}}(|H,b\rangle +|V,a\rangle )}$

${\displaystyle |V,a\rangle \rightarrow {\frac {1}{\sqrt {2}}}(|H,a\rangle -|V,b\rangle )}$

${\displaystyle |H,b\rangle \rightarrow {\frac {1}{\sqrt {2}}}(|H,b\rangle -|V,a\rangle )}$

${\displaystyle |V,b\rangle \rightarrow {\frac {1}{\sqrt {2}}}(|H,a\rangle +|V,b\rangle )}$

where ${\displaystyle |\lambda ,k\rangle }$ denotes a photon with polarization ${\displaystyle \lambda }$ on path ${\displaystyle k}$. In this way, we have the path of the photon entangled with its polarization. This is sometimes referred to as hyperentanglement, a situation in which the degrees of freedom of a single particle are entangled with each other. This, paired with the Hong-Ou-Mandel effect and projective measurements on the polarization state, can be used to create path entanglement between photons in a linear chain.

These one-dimensional chains of entangled photons still need to be connected via controlled-Z operations, similar to the KLM protocol. These controlled-Z connection s between chains are still probabilistic, relying on measurement dependent teleportation with special resource states. However, due to the fact that this method does not include Fock measurements on the photons being used for computation as the KLM protocol does, the probabilistic nature of implementing controlled-Z operations presents much less of a problem. In fact, as long as connections occur with probability greater than one half, the entanglement present between chains will be enough to perform useful quantum computation, on average.

Browne-Rudolph protocol

An alternative approach to building cluster states that focuses entirely on photon polarization is the Browne-Rudolph protocol. ^[5] This method rests on performing parity checks on a pair of photons to stitch together already entangled sets of photons, meaning that this protocol requires entangled photon sources. Browne and Rudolph proposed two ways of doing this, called type-I and type-II fusion.

Type-I fusion

In type-I fusion, photons with either vertical or horizontal polarization are injected into modes ${\displaystyle a}$ and ${\displaystyle b}$, connected by a polarizing beam splitter. Each of the photons sent into this system is part of a Bell pair that this method will try to entangle. Upon passing through the polarizing beam splitter, the two photons will go opposite ways if they have the same polarization or the same way if they have the opposite polarization, e.g.

${\displaystyle |H_{a},H_{b}\rangle \rightarrow |H_{a},H_{b}\rangle }$

or

${\displaystyle |H_{a},V_{b}\rangle \rightarrow |H_{a}V_{a},0_{b}\rangle }$

Then on one of these modes, a projective measurement onto the basis ${\displaystyle |H\rangle \pm |V\rangle }$ is performed. If the measurement is successful, i.e. if it detects anything, then the detected photon is destroyed, but the remaining photons from the Bell pairs become entangled. Failure to detect anything results in an effective loss of the involved photons in a way that breaks any chain of entangled photons they were on. This can make attempting to make connections between already developed chains potentially risky.

Type-II fusion

Type-II fusion works similarly to type-I fusion, with the differences being that a diagonal polarizing beam splitter is used and the pair of photons is measured in the two-qubit Bell basis. A successful measurement here involves measuring the pair to be in a Bell state with no relative phase between the superposition of states (e.g. ${\displaystyle |H,H\rangle +|V,V\rangle }$ as opposed to ${\displaystyle |H,H\rangle -|V,V\rangle }$). This again entangles any two clusters already formed. A failure here performs local complementation on the local subgraph, making an existing chain shorter rather than cutting it in half. In this way, while it requires the use of more qubits in combining entangled resources, the potential loss for attempts to connect two chains together are not as expensive for type-II fusion as they are for type-I fusion.

Computing with cluster states

Once a cluster state has been successfully generated, computation can be done with the resource state directly by applying measurements to the qubits on the lattice. This is the model of measurement-based quantum computation (MQC), and it is equivalent to the circuit model.

Logical operations in MQC come about from the byproduct operators that occur during quantum teleportation. For example, given a single qubit state ${\displaystyle |\psi \rangle }$, one can connect this qubit to a plus state ${\displaystyle |+\rangle =|0\rangle +|1\rangle }$ via a two-qubit controlled-Z operation. Then, upon measuring the first qubit (the original ${\displaystyle |\psi \rangle }$) in the Pauli-X basis, the original state of the first qubit is teleported to the second qubit with a measurement outcome dependent extra rotation, which one can see from the partial inner product of the measurement acting on the two-qubit state:

${\displaystyle (\left\langle +\right|Z^{m}\otimes I)CZ(\left|\psi \right\rangle \otimes \left|+\right\rangle )={\frac {1}{\sqrt {2}}}HZ^{m}\left|\psi \right\rangle }$.

for ${\displaystyle m=0,1}$ denoting the measurement outcome as either the ${\displaystyle +1}$ eigenstate of Pauli-X for ${\displaystyle m=0}$ or the ${\displaystyle -1}$ eigenstate for ${\displaystyle m=1}$. A two qubit state ${\displaystyle |\phi \rangle }$ connected by a pair of controlled-Z operations to the state ${\displaystyle CZ|+\rangle ^{\otimes 2}}$ yields a two-qubit operation on the teleported ${\displaystyle |\phi \rangle }$ state after measuring the original qubits:

${\displaystyle (\langle +|Z^{m_{1}}\otimes \langle +|Z^{m_{2}}\otimes I)CZ_{1,3}CZ_{2,4}(|\phi \rangle \otimes CZ|+\rangle ^{\otimes 2})={\frac {1}{2}}CZ(HZ^{m_{1}}\otimes HZ^{m_{2}})|\phi \rangle }$.

for measurement outcomes ${\displaystyle m_{1}}$ and ${\displaystyle m_{2}}$. This basic concept extends to arbitrarily many qubits, and thus computation is performed by the byproduct operators of teleportation down a chain. Adjusting the desired single-qubit gates is simply a matter of adjusting the measurement basis on each qubit, and non-Pauli measurements are necessary for universal quantum computation.

Experimental Implementations

Spatial encoding

Four-wave mixing can be thought of as the pair-wise absorption and emission of photons by the electrons in a material.

Path-entangled two qubit states have been generated in laboratory settings on silicon photonic chips in recent years, making important steps in the direction of generating optical cluster states. Among methods of doing this, it has been shown experimentally that spontaneous four-wave mixing can be used with the appropriate use of microring resonators and other waveguides for filtering to perform on-chip generation of two-photon Bell states, which are equivalent to two-qubit cluster states up to local unitary operations.

To do this, a short laser pulse is injected into an on-chip waveguide that splits into two paths. This forces the pulse into a superposition of the possible directions it could go. The two paths are coupled to microring resonators that allow circulation of the laser pulse until spontaneous four-wave mixing occurs, taking two photons from the laser pulse and converting them into a pair of photons, called the signal ${\displaystyle s}$ and idler ${\displaystyle i}$ with different frequencies in a way that conserves energy. In order to prevent the generation of multiple photon pairs at once, the procedure takes advantage of the conservation of energy and ensures that there is only enough energy in the laser pulse to create a single pair of photons. Because of this restriction, spontaneous four-wave mixing can only occur in one of the microring resonators at a time, meaning that the superposition of paths that the laser pulse could take is converted into a superposition of paths the two photons could be on. Mathematically, if ${\displaystyle |\alpha \rangle }$ denotes the laser pulse, the paths are labeled as ${\displaystyle a}$ and ${\displaystyle b}$, the process can be written as

${\displaystyle |\alpha \rangle \rightarrow {\frac {1}{\sqrt {2}}}(|\alpha _{a}\rangle +|\alpha _{b}\rangle )\rightarrow {\frac {1}{\sqrt {2}}}(|1_{s,a},0_{s,b},1_{i,a},0_{i,b}\rangle +|0_{s,a},1_{s,b},0_{i,a},1_{i,b}\rangle )={\frac {1}{\sqrt {2}}}(|00\rangle _{L}+|11\rangle _{L})}$

where ${\displaystyle |n_{x,y}\rangle }$ is the representation of having ${\displaystyle n}$ of photon ${\displaystyle x}$ on path ${\displaystyle y}$. With the state of the two photons being in this kind of superposition, they are entangled, which can be verified by tests of Bell inequalities.

Polarization encoding

Polarization entangled photon pairs have also been produced on-chip. ^[6] The setup involves a silicon wire waveguide that is split in half by a polarization rotator. This process, like the entanglement generation described for the dual rail encoding, makes use of the nonlinear process of spontaneous four-wave mixing, which can occur in the silicon wire on either side of the polarization rotator. However, the geometry of these wires are designed such that horizontal polarization is preferred in the conversion of laser pump photons to signal and idler photons. Thus when the photon pair is generated, both photons should have the same polarization, i.e.

${\displaystyle |\psi \rangle =|H_{s},H_{i}\rangle }$.

The polarization rotator is then designed with the specific dimensions such that horizontal polarization is switched to vertical polarization. Thus any pairs of photons generated before the rotator exit the waveguide with vertical polarization and any pairs generated on the other end of the wire exit the waveguide still having horizontal polarization. Mathematically, the process is, up to overall normalization,

${\displaystyle |\alpha \rangle \rightarrow |\alpha '\rangle +|H_{s},H_{i}\rangle \rightarrow |\alpha '\rangle +|V_{s},V_{i}\rangle \rightarrow |H_{s},H_{i}\rangle +e^{i\phi }|V_{s},V_{i}\rangle }$.

Assuming that equal space on each side of the rotator makes spontaneous four-wave mixing equally likely one each side, the output state of the photons is maximally entangled:

${\displaystyle |\psi \rangle ={\frac {1}{\sqrt {2}}}(|H_{s},H_{i}\rangle +e^{i\phi }|V_{s},V_{i}\rangle )={\frac {1}{\sqrt {2}}}(|00\rangle _{L}+e^{i\phi }|11\rangle _{L})}$.

States generated this way could potentially be used to build a cluster state using the Browne-Rudolph protocol.

References

1. Kok, Pieter; Munro, W. J.; Nemoto, Kae; Ralph, T. C.; Dowling, Jonathan P.; Milburn, G. J. (2007-01-24). "Linear optical quantum computing with photonic qubits". Reviews of Modern Physics. American Physical Society (APS). 79 (1): 135–174. arXiv: quant-ph/0512071 . Bibcode:2007RvMP...79..135K. doi:10.1103/revmodphys.79.135. ISSN   0034-6861. S2CID   119335959.
2. Rudolph, "Why I am optimistic about the silicon-photonic route to quantum computing", APL Photonics, 2017.
3. Nielsen, Michael A. (2004-07-21). "Optical Quantum Computation Using Cluster States". Physical Review Letters. American Physical Society (APS). 93 (4): 040503. arXiv: quant-ph/0402005 . Bibcode:2004PhRvL..93d0503N. doi:10.1103/physrevlett.93.040503. ISSN   0031-9007. PMID   15323741. S2CID   7720448.
4. Kok, Pieter; Munro, W. J.; Nemoto, Kae; Ralph, T. C.; Dowling, Jonathan P.; Milburn, G. J. (2007-01-24). "Linear optical quantum computing with photonic qubits". Reviews of Modern Physics. American Physical Society (APS). 79 (1): 135–174. arXiv: quant-ph/0512071 . Bibcode:2007RvMP...79..135K. doi:10.1103/revmodphys.79.135. ISSN   0034-6861. S2CID   119335959.
5. Browne, Daniel E.; Rudolph, Terry (2005-06-27). "Resource-Efficient Linear Optical Quantum Computation". Physical Review Letters. 95 (1): 010501. arXiv: quant-ph/0405157 . Bibcode:2005PhRvL..95a0501B. doi:10.1103/physrevlett.95.010501. ISSN   0031-9007. PMID   16090595. S2CID   27224760.
6. Matsuda, Nobuyuki; Le Jeannic, Hanna; Fukuda, Hiroshi; Tsuchizawa, Tai; Munro, William John; et al. (2012-11-12). "A monolithically integrated polarization entangled photon pair source on a silicon chip". Scientific Reports. 2 (1): 817. arXiv: 1211.2885 . Bibcode:2012NatSR...2E.817M. doi: 10.1038/srep00817 . ISSN   2045-2322. PMC   3495342 . PMID   23150781.