Related Research Articles
Control theory is a field of control engineering and applied mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any delay, overshoot, or steady-state error and ensuring a level of control stability; often with the aim to achieve a degree of optimality.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
Monte Carlo methods, or Monte Carlo experiments, are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results. The underlying concept is to use randomness to solve problems that might be deterministic in principle. They are often used in physical and mathematical problems and are most useful when it is difficult or impossible to use other approaches. Monte Carlo methods are mainly used in three problem classes: optimization, numerical integration, and generating draws from a probability distribution.
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field. It is called an inverse problem because it starts with the effects and then calculates the causes. It is the inverse of a forward problem, which starts with the causes and then calculates the effects.

Optimal control theory is a branch of control theory that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the Moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory.
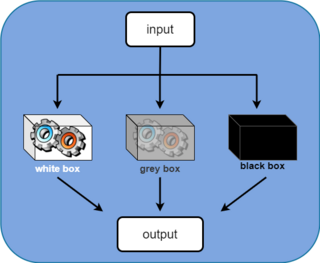
The field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data. System identification also includes the optimal design of experiments for efficiently generating informative data for fitting such models as well as model reduction. A common approach is to start from measurements of the behavior of the system and the external influences and try to determine a mathematical relation between them without going into many details of what is actually happening inside the system; this approach is called black box system identification.
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem where some of the constraints or the objective function are nonlinear. An optimization problem is one of calculation of the extrema of an objective function over a set of unknown real variables and conditional to the satisfaction of a system of equalities and inequalities, collectively termed constraints. It is the sub-field of mathematical optimization that deals with problems that are not linear.
Model predictive control (MPC) is an advanced method of process control that is used to control a process while satisfying a set of constraints. It has been in use in the process industries in chemical plants and oil refineries since the 1980s. In recent years it has also been used in power system balancing models and in power electronics. Model predictive controllers rely on dynamic models of the process, most often linear empirical models obtained by system identification. The main advantage of MPC is the fact that it allows the current timeslot to be optimized, while keeping future timeslots in account. This is achieved by optimizing a finite time-horizon, but only implementing the current timeslot and then optimizing again, repeatedly, thus differing from a linear–quadratic regulator (LQR). Also MPC has the ability to anticipate future events and can take control actions accordingly. PID controllers do not have this predictive ability. MPC is nearly universally implemented as a digital control, although there is research into achieving faster response times with specially designed analog circuitry.
Trajectory optimization is the process of designing a trajectory that minimizes some measure of performance while satisfying a set of constraints. Generally speaking, trajectory optimization is a technique for computing an open-loop solution to an optimal control problem. It is often used for systems where computing the full closed-loop solution is not required, impractical or impossible. If a trajectory optimization problem can be solved at a rate given by the inverse of the Lipschitz constant, then it can be used iteratively to generate a closed-loop solution in the sense of Caratheodory. If only the first step of the trajectory is executed for an infinite-horizon problem, then this is known as Model Predictive Control (MPC).
In mathematical optimization and related fields, relaxation is a modeling strategy. A relaxation is an approximation of a difficult problem by a nearby problem that is easier to solve. A solution of the relaxed problem provides information about the original problem.
The TOMLAB Optimization Environment is a modeling platform for solving applied optimization problems in MATLAB.
A geometric program (GP) is an optimization problem of the form
Advanced process monitor (APMonitor) is a modeling language for differential algebraic (DAE) equations. It is a free web-service or local server for solving representations of physical systems in the form of implicit DAE models. APMonitor is suited for large-scale problems and solves linear programming, integer programming, nonlinear programming, nonlinear mixed integer programming, dynamic simulation, moving horizon estimation, and nonlinear model predictive control. APMonitor does not solve the problems directly, but calls nonlinear programming solvers such as APOPT, BPOPT, IPOPT, MINOS, and SNOPT. The APMonitor API provides exact first and second derivatives of continuous functions to the solvers through automatic differentiation and in sparse matrix form.
The PROPT MATLAB Optimal Control Software is a new generation platform for solving applied optimal control and parameters estimation problems.
Moving horizon estimation (MHE) is an optimization approach that uses a series of measurements observed over time, containing noise and other inaccuracies, and produces estimates of unknown variables or parameters. Unlike deterministic approaches, MHE requires an iterative approach that relies on linear programming or nonlinear programming solvers to find a solution.
APOPT is a software package for solving large-scale optimization problems of any of these forms:
GPOPS-II is a general-purpose MATLAB software for solving continuous optimal control problems using hp-adaptive Gaussian quadrature collocation and sparse nonlinear programming. The acronym GPOPS stands for "General Purpose OPtimal Control Software", and the Roman numeral "II" refers to the fact that GPOPS-II is the second software of its type.
References
- ↑ MathWorks - Optimization Toolbox - Requirements
- ↑ Dragain, Andreas (2009). "Comparative Study of Numerical Methods for Optimal Control of a Biomechanical System" (PDF). Chalmers University of Technology. Retrieved 2013-07-01.
- ↑ Rao, Singiresu (2009). Engineering Optimization: Theory and Practice . Hoboken, New Jersey: John Wiley & Sons. p. 36. ISBN 978-0-470-18352-6.
- ↑ Banks, H.T.; et al. (2013). "Material parameter estimation and hypothesis testing on a 1D viscoelastic stenosis model: Methodology". Journal of Inverse and Ill-Posed Problems. 21 (1): 25–57. doi:10.1515/jip-2012-0081.
- ↑ Collins Licata, A.; et al. (2001). "A Physiologically Based Pharmacokinetic Model for Methyl tert-Butyl Ether in Humans: Implementing Sensitivity and Variability Analyses". Toxicological Sciences. 62 (2): 191–204. doi: 10.1093/toxsci/62.2.191 . PMID 11452131.
- ↑ Pachamanova, D. (2010). Simulation and Optimization in Finance + Web Site. Hoboken, New Jersey: John Wiley & Sons. ISBN 978-0-470-37189-3.
- ↑ Cartina, G.; et al. (2007). "Power System Analysis using MATLAB Toolboxes". 6th International Conference on Electromechanical and Power Systems: 305–308.