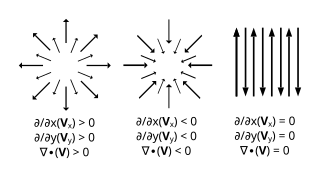
Del, or nabla, is an operator used in mathematics, in particular in vector calculus, as a vector differential operator, usually represented by the nabla symbol ∇. When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus. When applied to a field, it may denote the gradient of a scalar field, the divergence of a vector field, or the curl (rotation) of a vector field, depending on the way it is applied.
In mathematics, a Green's function of an inhomogeneous linear differential operator defined on a domain with specified initial conditions or boundary conditions is its impulse response.
In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants".

Scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value (scalar) that depends only on its location. A familiar example is potential energy due to gravity.
In mathematics, the directional derivative of a multivariate differentiable function along a given vector v at a given point x intuitively represents the instantaneous rate of change of the function, moving through x with a velocity specified by v. It therefore generalizes the notion of a partial derivative, in which the rate of change is taken along one of the curvilinear coordinate curves, all other coordinates being constant.
In mathematics, Green's identities are a set of three identities in vector calculus relating the bulk with the boundary of a region on which differential operators act. They are named after the mathematician George Green, who discovered Green's theorem.
Stochastic gradient descent, also known as incremental gradient descent, is an iterative method for optimizing a differentiable objective function, a stochastic approximation of gradient descent optimization. A 2018 article implicitly credits Herbert Robbins and Sutton Monro for developing SGD in their 1951 article titled "A Stochastic Approximation Method"; see Stochastic approximation for more information. It is called stochastic because samples are selected randomly instead of as a single group or in the order they appear in the training set.
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami operator, after Laplace and Eugenio Beltrami. Like the Laplacian, the Laplace–Beltrami operator is defined as the divergence of the gradient, and is a linear operator taking functions into functions. The operator can be extended to operate on tensors as the divergence of the covariant derivative. Alternatively, the operator can be generalized to operate on differential forms using the divergence and exterior derivative. The resulting operator is called the Laplace–de Rham operator.
In mathematics, the derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, and geometry.

In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over time. More formally, a flow is a group action of the real numbers on a set.
In mathematics, the Clark–Ocone theorem is a theorem of stochastic analysis. It expresses the value of some function F defined on the classical Wiener space of continuous paths starting at the origin as the sum of its mean value and an Itō integral with respect to that path. It is named after the contributions of mathematicians J.M.C. Clark (1970), Daniel Ocone (1984) and U.G. Haussmann (1978).

In mathematics, classical Wiener space is the collection of all continuous functions on a given domain, taking values in a metric space. Classical Wiener space is useful in the study of stochastic processes whose sample paths are continuous functions. It is named after the American mathematician Norbert Wiener.
In mathematics — specifically, in stochastic analysis — an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process. The generator is used in evolution equations such as the Kolmogorov backward equation ; its L2 Hermitian adjoint is used in evolution equations such as the Fokker–Planck equation.
In differential geometry there are a number of second-order, linear, elliptic differential operators bearing the name Laplacian. This article provides an overview of some of them.
In mathematics, the Skorokhod integral, often denoted δ, is an operator of great importance in the theory of stochastic processes. It is named after the Ukrainian mathematician Anatoliy Skorokhod. Part of its importance is that it unifies several concepts:
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral as well, although that is typically reserved for line integrals in the complex plane.