P-adic modular form

Last updated April 30, 2019

In mathematics, a p-adic modular form is a p-adic analog of a modular form, with coefficients that are p-adic numbers rather than complex numbers. Serre (1973) introduced p-adic modular forms as limits of ordinary modular forms, and Katz (1973) shortly afterwards gave a geometric and more general definition. Katz's p-adic modular forms include as special cases classical p-adic modular forms, which are more or less p-adic linear combinations of the usual "classical" modular forms, and overconvergent p-adic modular forms, which in turn include Hida's ordinary modular forms as special cases.

In mathematics, a modular form is a (complex) analytic function on the upper half-plane satisfying a certain kind of functional equation with respect to the group action of the modular group, and also satisfying a growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections with number theory. Modular forms appear in other areas, such as algebraic topology, sphere packing, and string theory.

Serre's definition

Serre defined a p-adic modular form to be a formal power series with p-adic coefficients that is a p-adic limit of classical modular forms with integer coefficients. The weights of these classical modular forms need not be the same; in fact, if they are then the p-adic modular form is nothing more than a linear combination of classical modular forms. In general the weight of a p-adic modular form is a p-adic number, given by the limit of the weights of the classical modular forms (in fact a slight refinement gives a weight in Z_p×Z/(p–1)Z).

The p-adic modular forms defined by Serre are special cases of those defined by Katz.

Katz's definition

A classical modular form of weight k can be thought of roughly as a function f from pairs (E,ω) of a complex elliptic curve with a holomorphic 1-form ω to complex numbers, such that f(E,λω) = λ^−kf(E,ω), and satisfying some additional conditions such as being holomorphic in some sense.

Katz's definition of a p-adic modular form is similar, except that E is now an elliptic curve over some algebra R (with p nilpotent) over the ring of integers R₀ of a finite extension of the p-adic numbers, such that E is not supersingular, in the sense that the Eisenstein series E_p–1 is invertible at (E,ω). The p-adic modular form f now takes values in R rather than in the complex numbers. The p-adic modular form also has to satisfy some other conditions analogous to the condition that a classical modular form should be holomorphic.

Overconvergent forms

Overconvergent p-adic modular forms are similar to the modular forms defined by Katz, except that the form has to be defined on a larger collection of elliptic curves. Roughly speaking, the value of the Eisenstein series E_k–1 on the form is no longer required to be invertible, but can be a smaller element of R. Informally the series for the modular form converges on this larger collection of elliptic curves, hence the name "overconvergent".

Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly. Originally defined for the modular group, Eisenstein series can be generalized in the theory of automorphic forms.

Related Research Articles

Elliptic curve an algebraic curve of genus 1 equipped with a basepoint

In mathematics, an elliptic curve is a plane algebraic curve defined by an equation of the form

In mathematics, the modularity theorem states that elliptic curves over the field of rational numbers are related to modular forms. Andrew Wiles proved the modularity theorem for semistable elliptic curves, which was enough to imply Fermat's last theorem. Later, Christophe Breuil, Brian Conrad, Fred Diamond and Richard Taylor extended Wiles' techniques to prove the full modularity theorem in 2001.

In mathematics, the Weil conjectures were some highly influential proposals by André Weil (1949), which led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.

The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings.

In mathematics, the Birch and Swinnerton-Dyer conjecture describes the set of rational solutions to equations defining an elliptic curve. It is an open problem in the field of number theory and is widely recognized as one of the most challenging mathematical problems. The conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay Mathematics Institute, which has offered a $1,000,000 prize for the first correct proof. It is named after mathematicians Bryan Birch and Peter Swinnerton-Dyer who developed the conjecture during the first half of the 1960s with the help of machine computation. As of 2018, only special cases of the conjecture have been proved.

In mathematics, in particular in the theory of modular forms, a Hecke operator, studied by Hecke (1937), is a certain kind of "averaging" operator that plays a significant role in the structure of vector spaces of modular forms and more general automorphic representations.

In mathematics, complex multiplication (CM) is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense. Put another way, it contains the theory of elliptic functions with extra symmetries, such as are visible when the period lattice is the Gaussian integer lattice or Eisenstein integer lattice.

In mathematics, the Sato–Tate conjecture is a statistical statement about the family of elliptic curves E_p over the finite field with p elements, with p a prime number, obtained from an elliptic curve E over the rational number field, by the process of reduction modulo a prime for almost all p. If N_p denotes the number of points on E_p and defined over the field with p elements, the conjecture gives an answer to the distribution of the second-order term for N_p. That is, by Hasse's theorem on elliptic curves we have

Neal I. Koblitz is a Professor of Mathematics at the University of Washington. He is also an adjunct professor with the Centre for Applied Cryptographic Research at the University of Waterloo. He is the creator of hyperelliptic curve cryptography and the independent co-creator of elliptic curve cryptography.

In mathematics, arithmetic geometry is roughly the application of techniques from algebraic geometry to problems in number theory. Arithmetic geometry is centered around Diophantine geometry, the study of rational points of algebraic varieties.

This is a glossary of arithmetic and diophantine geometry in mathematics, areas growing out of the traditional study of Diophantine equations to encompass large parts of number theory and algebraic geometry. Much of the theory is in the form of proposed conjectures, which can be related at various levels of generality.

A modular elliptic curve is an elliptic curve E that admits a parametrisation X₀(N) → E by a modular curve. This is not the same as a modular curve that happens to be an elliptic curve, and which could be called an elliptic modular curve. The modularity theorem, also known as the Taniyama–Shimura conjecture, asserts that every elliptic curve defined over the rational numbers is modular.

In mathematics, overconvergent modular forms are special p-adic modular forms that are elements of certain p-adic Banach spaces containing classical spaces of modular forms as subspaces. They were introduced by Nicholas M. Katz in 1972.

In mathematics, a p-adic zeta function, or more generally a p-adic L-function, is a function analogous to the Riemann zeta function, or more general L-functions, but whose domain and target are p-adic. For example, the domain could be the p-adic integersZ_p, a profinite p-group, or a p-adic family of Galois representations, and the image could be the p-adic numbersQ_p or its algebraic closure.

In arithmetic geometry, the Tate–Shafarevich group Ш(A/K), introduced by Serge Lang and John Tate (1958) and Igor Shafarevich (1959), of an abelian variety A (or more generally a group scheme) defined over a number field K consists of the elements of the Weil–Châtelet group WC(A/K) = H¹(G_K, A) that become trivial in all of the completions of K (i.e. the p-adic fields obtained from K, as well as its real and complex completions). Thus, in terms of Galois cohomology, it can be written as

In mathematics, the Hodge bundle, named after W. V. D. Hodge, appears in the study of families of curves, where it provides an invariant in the moduli theory of algebraic curves. Furthermore, it has applications to the theory of modular forms on reductive algebraic groups and string theory.

In mathematics, the Tate curve is a curve defined over the ring of formal power series $with integer coefficients. Over the open subscheme where q is invertible, the Tate curve is an elliptic curve. The Tate curve can also be defined for q as an element of a complete field of norm less than 1, in which case the formal power series converge.$

In mathematics, the q-expansion principle states that a modular form has coefficients in some module provided that its q-expansion at enough cusps resembles that of such a form. It was introduced by Katz.

In mathematics, almost holomorphic modular forms, also called nearly holomorphic modular forms, are a generalization of modular forms that are polynomials in 1/Im(τ) with coefficients that are holomorphic functions of τ. A quasimodular form is the holomorphic part of an almost holomorphic modular form. An almost holomorphic modular form is determined by its holomorphic part, so the operation of taking the holomorphic part gives an isomorphism between the spaces of almost holomorphic modular forms and quasimodular forms. The archetypal examples of quasimodular forms are the Eisenstein series E₂(τ) (the holomorphic part of the almost holomorphic modular form E₂(τ) – 3/πIm(τ)), and derivatives of modular forms.

References

Coleman, Robert F. (1996), "Classical and overconvergent modular forms", Inventiones Mathematicae , 124 (1): 215–241, doi:10.1007/s002220050051, ISSN 0020-9910, MR 1369416
Gouvêa, Fernando Q. (1988), Arithmetic of p-adic modular forms, Lecture Notes in Mathematics, 1304, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0082111, ISBN 978-3-540-18946-6, MR 1027593
Hida, Haruzo (2004), p-adic automorphic forms on Shimura varieties, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-20711-7, MR 2055355
Katz, Nicholas M. (1973), "p-adic properties of modular schemes and modular forms", Modular functions of one variable, III (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, 350, Berlin, New York: Springer-Verlag, pp. 69–190, doi:10.1007/978-3-540-37802-0_3, ISBN 978-3-540-06483-1, MR 0447119
Serre, Jean-Pierre (1973), "Formes modulaires et fonctions zêta p-adiques", Modular functions of one variable, III (Proc. Internat. Summer School, Univ. Antwerp, 1972), Lecture Notes in Math., 350, Berlin, New York: Springer-Verlag, pp. 191–268, doi:10.1007/978-3-540-37802-0_4, ISBN 978-3-540-06483-1, 0404145

<i>Inventiones Mathematicae</i> mathematical journal

Inventiones Mathematicae is a mathematical journal published monthly by Springer Science+Business Media. It was established in 1966 and is regarded as one of the most prestigious mathematics journals in the world. As of 2016, the managing editors are Helmut Hofer and Jean-Benoît Bost.

In computing, a Digital Object Identifier or DOI is a persistent identifier or handle used to identify objects uniquely, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.

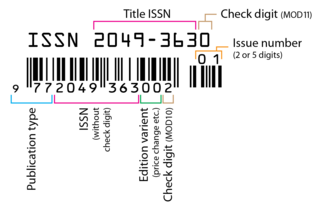
International Standard Serial Number unique eight-digit number used to identify a print or electronic periodical publication

An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication, such as a magazine. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.