In physics, the cross section is a measure of the probability that a specific process will take place when some kind of radiant excitation intersects a localized phenomenon. For example, the Rutherford cross-section is a measure of probability that an alpha-particle will be deflected by a given angle during a collision with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of transverse area. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.
Dynamic mechanical analysis is a technique used to study and characterize materials. It is most useful for studying the viscoelastic behavior of polymers. A sinusoidal stress is applied and the strain in the material is measured, allowing one to determine the complex modulus. The temperature of the sample or the frequency of the stress are often varied, leading to variations in the complex modulus; this approach can be used to locate the glass transition temperature of the material, as well as to identify transitions corresponding to other molecular motions.
In quantum field theory, the Dirac spinor is the spinor that describes all known fundamental particles that are fermions, with the possible exception of neutrinos. It appears in the plane-wave solution to the Dirac equation, and is a certain combination of two Weyl spinors, specifically, a bispinor that transforms "spinorially" under the action of the Lorentz group.
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
Hemorheology, also spelled haemorheology, or blood rheology, is the study of flow properties of blood and its elements of plasma and cells. Proper tissue perfusion can occur only when blood's rheological properties are within certain levels. Alterations of these properties play significant roles in disease processes. Blood viscosity is determined by plasma viscosity, hematocrit and mechanical properties of red blood cells. Red blood cells have unique mechanical behavior, which can be discussed under the terms erythrocyte deformability and erythrocyte aggregation. Because of that, blood behaves as a non-Newtonian fluid. As such, the viscosity of blood varies with shear rate. Blood becomes less viscous at high shear rates like those experienced with increased flow such as during exercise or in peak-systole. Therefore, blood is a shear-thinning fluid. Contrarily, blood viscosity increases when shear rate goes down with increased vessel diameters or with low flow, such as downstream from an obstruction or in diastole. Blood viscosity also increases with increases in red cell aggregability.

A granular material is a conglomeration of discrete solid, macroscopic particles characterized by a loss of energy whenever the particles interact. The constituents that compose granular material are large enough such that they are not subject to thermal motion fluctuations. Thus, the lower size limit for grains in granular material is about 1 μm. On the upper size limit, the physics of granular materials may be applied to ice floes where the individual grains are icebergs and to asteroid belts of the Solar System with individual grains being asteroids.
In physics, the Hamilton–Jacobi equation, named after William Rowan Hamilton and Carl Gustav Jacob Jacobi, is an alternative formulation of classical mechanics, equivalent to other formulations such as Newton's laws of motion, Lagrangian mechanics and Hamiltonian mechanics. The Hamilton–Jacobi equation is particularly useful in identifying conserved quantities for mechanical systems, which may be possible even when the mechanical problem itself cannot be solved completely.

Soil mechanics is a branch of soil physics and applied mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids and other matter. Along with rock mechanics, soil mechanics provides the theoretical basis for analysis in geotechnical engineering, a subdiscipline of civil engineering, and engineering geology, a subdiscipline of geology. Soil mechanics is used to analyze the deformations of and flow of fluids within natural and man-made structures that are supported on or made of soil, or structures that are buried in soils. Example applications are building and bridge foundations, retaining walls, dams, and buried pipeline systems. Principles of soil mechanics are also used in related disciplines such as geophysical engineering, coastal engineering, agricultural engineering, hydrology and soil physics.
Dynamic modulus is the ratio of stress to strain under vibratory conditions. It is a property of viscoelastic materials.
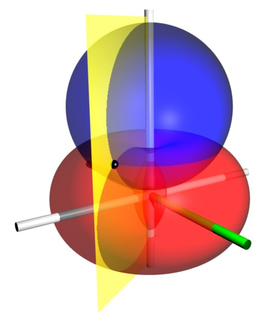
Bispherical coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional bipolar coordinate system about the axis that connects the two foci. Thus, the two foci and in bipolar coordinates remain points in the bispherical coordinate system.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927.
An a priori probability is a probability that is derived purely by deductive reasoning. One way of deriving a priori probabilities is the principle of indifference, which has the character of saying that, if there are N mutually exclusive and collectively exhaustive events and if they are equally likely, then the probability of a given event occurring is 1/N. Similarly the probability of one of a given collection of K events is K / N.
Electroacoustic phenomena arise when ultrasound propagates through a fluid containing ions. The associated particle motion generates electric signals because ions have electric charge. This coupling between ultrasound and electric field is called electroacoustic phenomena. The fluid might be a simple Newtonian liquid, or complex heterogeneous dispersion, emulsion or even a porous body. There are several different electroacoustic effects depending on the nature of the fluid.
Sedimentation potential occurs when dispersed particles move under the influence of either gravity or centrifugation in a medium. This motion disrupts the equilibrium symmetry of the particle's double layer. While the particle moves, the ions in the electric double layer lag behind due to the liquid flow. This causes a slight displacement between the surface charge and the electric charge of the diffuse layer. As a result, the moving particle creates a dipole moment. The sum of all of the dipoles generates an electric field which is called sedimentation potential. It can be measured with an open electrical circuit, which is also called sedimentation current.
In linear elasticity, the equations describing the deformation of an elastic body subject only to surface forces on the boundary are the equilibrium equation:
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
In quantum field theory, a non-topological soliton (NTS) is a soliton field configuration possessing, contrary to a topological one, a conserved Noether charge and stable against transformation into usual particles of this field for the following reason. For fixed charge Q, the mass sum of Q free particles exceeds the energy (mass) of the NTS so that the latter is energetically favorable to exist.

A force-sensing resistor is a material whose resistance changes when a force, pressure or mechanical stress is applied. They are also known as "force-sensitive resistor" and are sometimes referred to by the initialism "FSR".
Lagrangian field theory is a formalism in classical field theory. It is the field-theoretic analogue of Lagrangian mechanics. Lagrangian mechanics is used to analyze the motion of a system of discrete particles each with a finite number of degrees of freedom. Lagrangian field theory applies to continua and fields, which have an infinite number of degrees of freedom.
Anelasticity is a property of materials that describes their behaviour when undergoing deformation. Its formal definition does not include the physical or atomistic mechanisms but still interprets the anelastic behaviour as a manifestation of internal relaxation processes. It's a special case of elastic behaviour.














