
In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The 'order' of the magic square is the number of integers along one side (n), and the constant sum is called the 'magic constant'. If the array includes just the positive integers , the magic square is said to be 'normal'. Some authors take magic square to mean normal magic square.
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.
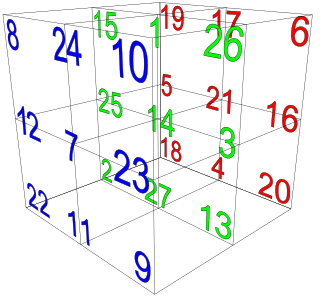
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a collection of integers arranged in an n × n × n pattern such that the sums of the numbers on each row, on each column, on each pillar and on each of the four main space diagonals are equal, the so-called magic constant of the cube, denoted M3(n). It can be shown that if a magic cube consists of the numbers 1, 2, ..., n3, then it has magic constant (sequence A027441 in the OEIS)
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars, and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant.
In mathematics, a P-multimagic square is a magic square that remains magic even if all its numbers are replaced by their kth powers for 1 ≤ k ≤ P. 2-multimagic squares are called bimagic, 3-multimagic squares are called trimagic, 4-multimagic squares tetramagic, and 5-multimagic squares pentamagic.
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares and magic cubes, that is, an n × n × n × ... × n array of integers such that the sums of the numbers on each pillar (along any axis) as well as on the main space diagonals are all the same. The common sum is called the magic constant of the hypercube, and is sometimes denoted Mk(n). If a magic hypercube consists of the numbers 1, 2, ..., nk, then it has magic number

The 15 puzzle is a sliding puzzle having 15 square tiles numbered 1–15 in a frame that is 4 tile positions high and 4 positions wide, leaving one unoccupied position. Tiles in the same row or column of the open position can be moved by sliding them horizontally or vertically, respectively. The goal of the puzzle is to place the tiles in numerical order.
A pandiagonal magic square or panmagic square is a magic square with the additional property that the broken diagonals, i.e. the diagonals that wrap round at the edges of the square, also add up to the magic constant.

A most-perfect magic square of order n is a magic square containing the numbers 1 to n2 with two additional properties:
- Each 2 × 2 subsquare sums to 2s, where s = n2 + 1.
- All pairs of integers distant n/2 along a (major) diagonal sum to s.
An antimagic square of order n is an arrangement of the numbers 1 to n2 in a square, such that the sums of the n rows, the n columns and the two diagonals form a sequence of 2n + 2 consecutive integers. The smallest antimagic squares have order 4. Antimagic squares contrast with magic squares, where each row, column, and diagonal sum must have the same value.
John Robert Hendricks was a Canadian amateur mathematician specializing in magic squares and hypercubes. He published many articles in the Journal of Recreational Mathematics as well as other journals.

In geometry, a space diagonal of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face as each other.
Every magic cube may be assigned to one of six magic cube classes, based on the cube characteristics.
A pantriagonal magic cube is a magic cube where all 4m2 pantriagonals sum correctly. There are 4 one-segment pantriagonals, 12(m − 1) two-segment pantriagonals, and 4(m − 2)(m − 1) three-segment pantriagonals. This class of magic cubes may contain some simple magic squares and/or pandiagonal magic squares, but not enough to satisfy any other classifications.
The class of diagonal magic cubes is the second of the six magic cube classes, coming after the simple magic cubes.
In recreational mathematics and the theory of magic squares, a broken diagonal is a set of n cells forming two parallel diagonal lines in the square. Alternatively, these two lines can be thought of as wrapping around the boundaries of the square to form a single sequence.

An associative magic square is a magic square for which each pair of numbers symmetrically opposite to the center sum up to the same value. For an n × n square, filled with the numbers from 1 to n2, this common sum must equal n2 + 1. These squares are also called associated magic squares, regular magic squares, regmagic squares, or symmetric magic squares.

A simple magic cube is the lowest of six basic classes of magic cubes. These classes are based on extra features required.
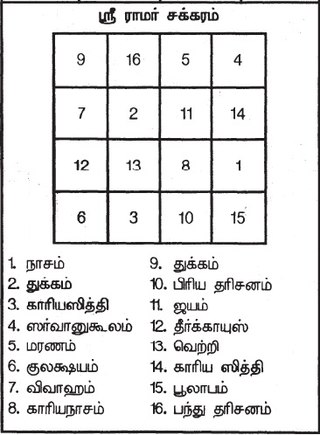
Sriramachakra is a mystic diagram or a yantra given in Tamil almanacs as an instrument of astrology for predicting one's future. The geometrical diagram consists of a square divided into smaller squares by equal numbers of lines parallel to the sides of the square. Certain integers in well defined patterns are written in the various smaller squares. In some almanacs, for example, in the Panchangam published by the Sringeri Sharada Peetham or the Pnachangam published by Srirangam Temple, the diagram takes the form of a magic square of order 4 with certain special properties. This magic square belongs to a certain class of magic squares called strongly magic squares which has been so named and studied by T V Padmakumar, an amateur mathematician from Thiruvananthapuram, Kerala. In some almanacs, for example, in the Pambu Panchangam, the diagram consists of an arrangement of 36 small squares in 6 rows and 6 columns in which the digits 1, 2, ..., 9 are written in that order from left to right starting from the top-left corner, repeating the digits in the same direction once the digit 9 is reached.

A geometric magic square, often abbreviated to geomagic square, is a generalization of magic squares invented by Lee Sallows in 2001. A traditional magic square is a square array of numbers whose sum taken in any row, any column, or in either diagonal is the same target number. A geomagic square, on the other hand, is a square array of geometrical shapes in which those appearing in each row, column, or diagonal can be fitted together to create an identical shape called the target shape. As with numerical types, it is required that the entries in a geomagic square be distinct. Similarly, the eight trivial variants of any square resulting from its rotation and/or reflection are all counted as the same square. By the dimension of a geomagic square is meant the dimension of the pieces it uses. Hitherto interest has focused mainly on 2D squares using planar pieces, but pieces of any dimension are permitted.








