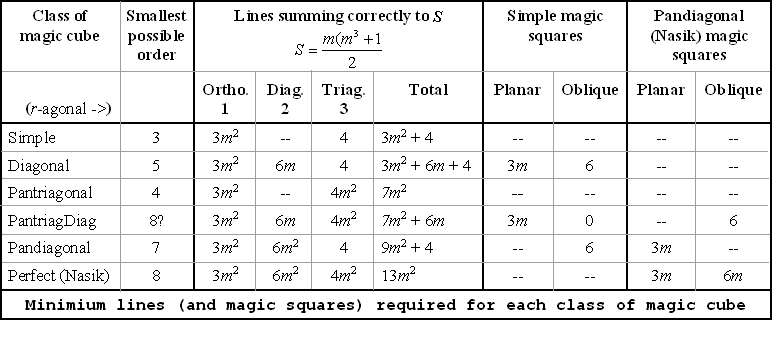
The six classes
The minimum requirements for a magic cube are: all rows, columns, pillars, and 4 space diagonals must sum to the same value. A simple magic cube contains no magic squares or not enough to qualify for the next class.
The smallest normal simple magic cube is order 3. Minimum correct summations required = 3m2 + 4
Each of the 3m planar arrays must be a simple magic square. The 6 oblique squares are also simple magic. The smallest normal diagonal magic cube is order 5.
These squares were referred to as 'Perfect' by Gardner and others. At the same time he referred to Langman’s 1962 pandiagonal cube also as 'Perfect'.
Christian Boyer and Walter Trump now consider this and the next two classes to be Perfect. (See Alternate Perfect below).
A. H. Frost referred to all but the simple class as Nasik cubes.
The smallest normal diagonal magic cube is order 5; see Diagonal magic cube. Minimum correct summations required = 3m2 + 6m + 4
All 4m2 pantriagonals must sum correctly (that is 4 one-segment, 12(m−1) two-segment, and 4(m−2)(m−1) three-segment). There may be some simple AND/OR pandiagonal magic squares, but not enough to satisfy any other classification.
The smallest normal pantriagonal magic cube is order 4; see Pantriagonal magic cube.
Minimum correct summations required = 7m2. All pan-r-agonals sum correctly for r = 1 and 3.
A cube of this class was first constructed in late 2004 by Mitsutoshi Nakamura. This cube is a combination pantriagonal magic cube and diagonal magic cube. Therefore, all main and broken space diagonals sum correctly, and it contains 3m planar simple magic squares. In addition, all 6 oblique squares are pandiagonal magic squares. The only such cube constructed so far is order 8. It is not known what other orders are possible; see Pantriagdiag magic cube. Minimum correct summations required = 7m2 + 6m
All 3m planar arrays must be pandiagonal magic squares. The 6 oblique squares are always magic (usually simple magic). Several of them may be pandiagonal magic. Gardner also called this (Langman’s pandiagonal) a 'perfect' cube, presumably not realizing it was a higher class then Myer’s cube. See previous note re Boyer and Trump.
The smallest normal pandiagonal magic cube is order 7; see Pandiagonal magic cube.
Minimum correct summations required = 9m2 + 4. All pan-r-agonals sum correctly for r = 1 and 2.
All 3m planar arrays must be pandiagonal magic squares. In addition, all pantriagonals must sum correctly. These two conditions combine to provide a total of 9m pandiagonal magic squares.
The smallest normal perfect magic cube is order 8; see Perfect magic cube.
Nasik; A. H. Frost (1866) referred to all but the simple magic cube as Nasik!
C. Planck (1905) redefined Nasik to mean magic hypercubes of any order or dimension in which all possible lines summed correctly.
i.e. Nasik is a preferred alternate, and less ambiguous term for the perfect class.
Minimum correct summations required = 13m2. All pan-r-agonals sum correctly for r = 1, 2 and 3.
Alternate Perfect Note that the above is a relatively new definition of perfect. Until about 1995 there was much confusion about what constituted a perfect magic cube (see the discussion under Diagonal).
Included below are references and links to discussions of the old definition
With the popularity of personal computers it became easier to examine the finer details of magic cubes. Also more and more work was being done with higher-dimension magic hypercubes. For example, John Hendricks constructed the world's first Nasik magic tesseract in 2000. Classed as a perfect magic tesseract by Hendricks definition.

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.

In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells, meeting at right angles. The tesseract is one of the six convex regular 4-polytopes.

In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .

In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The 'order' of the magic square is the number of integers along one side (n), and the constant sum is called the 'magic constant'. If the array includes just the positive integers , the magic square is said to be 'normal'. Some authors take magic square to mean normal magic square.
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.

Squaring the square is the problem of tiling an integral square using only other integral squares. The name was coined in a humorous analogy with squaring the circle. Squaring the square is an easy task unless additional conditions are set. The most studied restriction is that the squaring be perfect, meaning the sizes of the smaller squares are all different. A related problem is squaring the plane, which can be done even with the restriction that each natural number occurs exactly once as a size of a square in the tiling. The order of a squared square is its number of constituent squares.
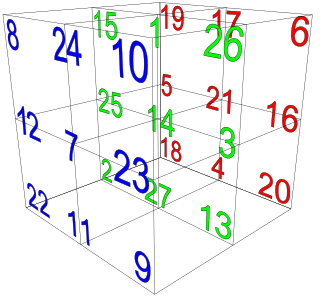
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a collection of integers arranged in an n × n × n pattern such that the sums of the numbers on each row, on each column, on each pillar and on each of the four main space diagonals are equal, the so-called magic constant of the cube, denoted M3(n). It can be shown that if a magic cube consists of the numbers 1, 2, ..., n3, then it has magic constant (sequence A027441 in the OEIS)
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars, and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant.
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares and magic cubes, that is, an n × n × n × ... × n array of integers such that the sums of the numbers on each pillar (along any axis) as well as on the main space diagonals are all the same. The common sum is called the magic constant of the hypercube, and is sometimes denoted Mk(n). If a magic hypercube consists of the numbers 1, 2, ..., nk, then it has magic number
John Robert Hendricks was a Canadian amateur mathematician notable for his work in magic squares and hypercubes. He published many articles in the Journal of Recreational Mathematics as well as other mathematics-related journals.

In geometry, a space diagonal of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face as each other.
A pantriagonal magic cube is a magic cube where all 4m2 pantriagonals sum correctly. There are 4 one-segment pantriagonals, 12(m − 1) two-segment pantriagonals, and 4(m − 2)(m − 1) three-segment pantriagonals. This class of magic cubes may contain some simple magic squares and/or pandiagonal magic squares, but not enough to satisfy any other classifications.
The class of diagonal magic cubes is the second of the six magic cube classes, coming after the simple magic cubes.
In recreational mathematics, a pandiagonal magic cube is a magic cube with the additional property that all broken diagonals have the same sum as each other. Pandiagonal magic cubes are extensions of diagonal magic cubes and generalize pandiagonal magic squares to three dimensions.
5 (five) is a number, numeral and digit. It is the natural number, and cardinal number, following 4 and preceding 6, and is a prime number. It has garnered attention throughout history in part because distal extremities in humans typically contain five digits.
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
In geometry, a 6-cube is a six-dimensional hypercube with 64 vertices, 192 edges, 240 square faces, 160 cubic cells, 60 tesseract 4-faces, and 12 5-cube 5-faces.
In geometry, an 8-cube is an eight-dimensional hypercube. It has 256 vertices, 1024 edges, 1792 square faces, 1792 cubic cells, 1120 tesseract 4-faces, 448 5-cube 5-faces, 112 6-cube 6-faces, and 16 7-cube 7-faces.

A simple magic cube is the lowest of six basic classes of magic cubes. These classes are based on extra features required.

In geometry of 4 dimensions or higher, a proprism is a polytope resulting from the Cartesian product of two or more polytopes, each of two dimensions or higher. The term was coined by John Horton Conway for product prism. The dimension of the space of a proprism equals the sum of the dimensions of all its product elements. Proprisms are often seen as k-face elements of uniform polytopes.