A simple magic cube is the lowest of six basic classes of magic cubes. These classes are based on extra features required.
The simple magic cube requires only the basic features a cube requires to be magic. Namely, all lines parallel to the faces, and all 4 space diagonals sum correctly. [1] i.e. all "1-agonals" and all "3-agonals" sum to
No planar diagonals (2-agonals) are required to sum correctly, so there are probably no magic squares in the cube.
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets, or sides, with three meeting at each vertex. Viewed from a corner, it is a hexagon and its net is usually depicted as a cross.
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.
In geometry, a hypercube is an n-dimensional analogue of a square and a cube. It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to .
In recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The 'order' of the magic square is the number of integers along one side (n), and the constant sum is called the 'magic constant'. If the array includes just the positive integers , the magic square is said to be 'normal'. Some authors take magic square to mean normal magic square.
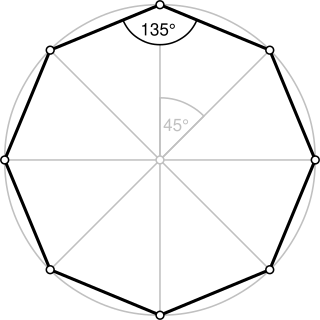
In geometry, an octagon is an eight-sided polygon or 8-gon.
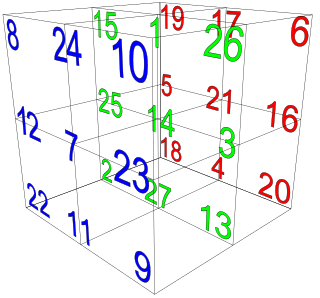
In mathematics, a magic cube is the 3-dimensional equivalent of a magic square, that is, a collection of integers arranged in an n × n × n pattern such that the sums of the numbers on each row, on each column, on each pillar and on each of the four main space diagonals are equal, the so-called magic constant of the cube, denoted M3(n). It can be shown that if a magic cube consists of the numbers 1, 2, ..., n3, then it has magic constant (sequence A027441 in the OEIS)
In mathematics, a perfect magic cube is a magic cube in which not only the columns, rows, pillars, and main space diagonals, but also the cross section diagonals sum up to the cube's magic constant.
In mathematics, a magic hypercube is the k-dimensional generalization of magic squares and magic cubes, that is, an n × n × n × ... × n array of integers such that the sums of the numbers on each pillar (along any axis) as well as on the main space diagonals are all the same. The common sum is called the magic constant of the hypercube, and is sometimes denoted Mk(n). If a magic hypercube consists of the numbers 1, 2, ..., nk, then it has magic number
The magic constant or magic sum of a magic square is the sum of numbers in any row, column, or diagonal of the magic square. For example, the magic square shown below has a magic constant of 15. For a normal magic square of order n – that is, a magic square which contains the numbers 1, 2, ..., n2 – the magic constant is .
An antimagic square of order n is an arrangement of the numbers 1 to n2 in a square, such that the sums of the n rows, the n columns and the two diagonals form a sequence of 2n + 2 consecutive integers. The smallest antimagic squares have order 4. Antimagic squares contrast with magic squares, where each row, column, and diagonal sum must have the same value.
John Robert Hendricks was a Canadian amateur mathematician notable for his work in magic squares and hypercubes. He published many articles in the Journal of Recreational Mathematics as well as other mathematics-related journals.
In geometry, a space diagonal of a polyhedron is a line connecting two vertices that are not on the same face. Space diagonals contrast with face diagonals, which connect vertices on the same face as each other.
Every magic cube may be assigned to one of six magic cube classes, based on the cube characteristics.
A pantriagonal magic cube is a magic cube where all 4m2 pantriagonals sum correctly. There are 4 one-segment pantriagonals, 12(m − 1) two-segment pantriagonals, and 4(m − 2)(m − 1) three-segment pantriagonals. This class of magic cubes may contain some simple magic squares and/or pandiagonal magic squares, but not enough to satisfy any other classifications.
The class of diagonal magic cubes is the second of the six magic cube classes, coming after the simple magic cubes.
In recreational mathematics, a pandiagonal magic cube is a magic cube with the additional property that all broken diagonals have the same sum as each other. Pandiagonal magic cubes are extensions of diagonal magic cubes and generalize pandiagonal magic squares to three dimensions.
In lattice field theory, staggered fermions are a fermion discretization that reduces the number of fermion doublers from sixteen to four. They are one of the fastest lattice fermions when it comes to simulations and they also possess some nice features such as a remnant chiral symmetry, making them very popular in lattice QCD calculations. Staggered fermions were first formulated by John Kogut and Leonard Susskind in 1975 and were later found to be equivalent to the discretized version of the Dirac–Kähler fermion.
In five-dimensional geometry, a 5-cube is a name for a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
The Siamese method, or De la Loubère method, is a simple method to construct any size of n-odd magic squares. The method was brought to France in 1688 by the French mathematician and diplomat Simon de la Loubère, as he was returning from his 1687 embassy to the kingdom of Siam. The Siamese method makes the creation of magic squares straightforward.
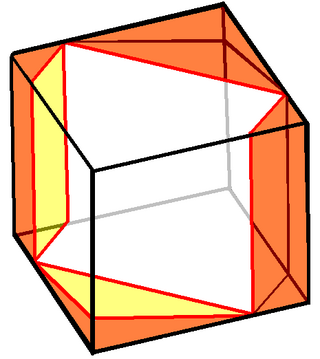
In geometry, Prince Rupert's cube is the largest cube that can pass through a hole cut through a unit cube without splitting it into two pieces. Its side length is approximately 1.06, 6% larger than the side length 1 of the unit cube through which it passes. The problem of finding the largest square that lies entirely within a unit cube is closely related, and has the same solution.
