An alphamagic square is a magic square that remains magic when its numbers are replaced by the number of letters occurring in the name of each number. Hence 3 would be replaced by 5, the number of letters in "three". Since different languages will have a different number of letters for the spelling of the same number, alphamagic squares are language-dependent. [1] The term alphamagic was coined by Lee Sallows in 1986. [2] [3]
The example below is alphamagic. To find out if a magic square is also an alphamagic square, convert it into the array of corresponding number words. For example,
| 5 | 22 | 18 |
| 28 | 15 | 2 |
| 12 | 8 | 25 |
converts to ...
| five | twenty-two | eighteen |
| twenty-eight | fifteen | two |
| twelve | eight | twenty-five |
Counting the letters in each number word generates the following square which turns out to also be magic:
| 4 | 9 | 8 |
| 11 | 7 | 3 |
| 6 | 5 | 10 |
If the generated array is also a magic square, the original square is alphamagic. In 2017 British computer scientist Chris Patuzzo discovered several doubly alphamagic squares in which the generated square is in turn an alphamagic square. [4]
The above example enjoys another special property: the nine numbers in the lower square are consecutive. This prompted Martin Gardner to describe it as "Surely the most fantastic magic square ever discovered." [5]
Sallows has produced a still more magical version—a square which is both geomagic and alphamagic. In the square shown in Figure 1, any three shapes in a straight line—including the diagonals—tile the cross; thus the square is geomagic. The number of letters in the number names printed on any three shapes in a straight line sum to forty five; thus the square is alphamagic.
The Universal Book of Mathematics provides the following information about Alphamagic Squares: [6] [7]
In 2018, the first 3 × 3 Russian alphamagic square was found by Jamal Senjaya. Following that, another 158 3 × 3 Russian alphamagic squares were found (by the same person) where the entries do not exceed 300.
MATLAB is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages.
Metafont is a description language used to define raster fonts. It is also the name of the interpreter that executes Metafont code, generating the bitmap fonts that can be embedded into e.g. PostScript. Metafont was devised by Donald Knuth as a companion to his TeX typesetting system.
In mathematics, especially historical and recreational mathematics, a square array of numbers, usually positive integers, is called a magic square if the sums of the numbers in each row, each column, and both main diagonals are the same. The "order" of the magic square is the number of integers along one side (n), and the constant sum is called the "magic constant". If the array includes just the positive integers , the magic square is said to be "normal". Some authors take "magic square" to mean "normal magic square".
The Ulam spiral or prime spiral is a graphical depiction of the set of prime numbers, devised by mathematician Stanisław Ulam in 1963 and popularized in Martin Gardner's Mathematical Games column in Scientific American a short time later. It is constructed by writing the positive integers in a square spiral and specially marking the prime numbers.
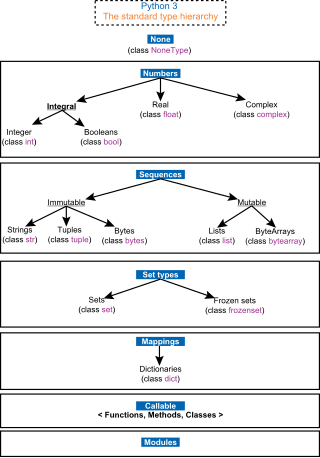
In computer science and computer programming, a data type is a collection or grouping of data values, usually specified by a set of possible values, a set of allowed operations on these values, and/or a representation of these values as machine types. A data type specification in a program constrains the possible values that an expression, such as a variable or a function call, might take. On literal data, it tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers, floating-point numbers, characters and Booleans.
In geometry, flexagons are flat models, usually constructed by folding strips of paper, that can be flexed or folded in certain ways to reveal faces besides the two that were originally on the back and front.
19 (nineteen) is the natural number following 18 and preceding 20. It is a prime number.
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called tiles, with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety of geometries.
In combinatorial mathematics, two Latin squares of the same size (order) are said to be orthogonal if when superimposed the ordered paired entries in the positions are all distinct. A set of Latin squares, all of the same order, all pairs of which are orthogonal is called a set of mutually orthogonal Latin squares. This concept of orthogonality in combinatorics is strongly related to the concept of blocking in statistics, which ensures that independent variables are truly independent with no hidden confounding correlations. "Orthogonal" is thus synonymous with "independent" in that knowing one variable's value gives no further information about another variable's likely value.
A pandiagonal magic square or panmagic square is a magic square with the additional property that the broken diagonals, i.e. the diagonals that wrap round at the edges of the square, also add up to the magic constant.
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is the chairman of the OEIS Foundation.
Dattatreya Ramchandra Kaprekar was an Indian recreational mathematician who described several classes of natural numbers including the Kaprekar, harshad and self numbers and discovered the Kaprekar's constant, named after him. Despite having no formal postgraduate training and working as a schoolteacher, he published extensively and became well known in recreational mathematics circles.
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence, construction and properties of systems of finite sets whose arrangements satisfy generalized concepts of balance and/or symmetry. These concepts are not made precise so that a wide range of objects can be thought of as being under the same umbrella. At times this might involve the numerical sizes of set intersections as in block designs, while at other times it could involve the spatial arrangement of entries in an array as in sudoku grids.
The programming language APL is distinctive in being symbolic rather than lexical: its primitives are denoted by symbols, not words. These symbols were originally devised as a mathematical notation to describe algorithms. APL programmers often assign informal names when discussing functions and operators but the core functions and operators provided by the language are denoted by non-textual symbols.
Lee Cecil Fletcher Sallows is a British electronics engineer known for his contributions to recreational mathematics. He is particularly noted as the inventor of golygons, self-enumerating sentences, and geomagic squares.
In the geometry of tessellations, a rep-tile or reptile is a shape that can be dissected into smaller copies of the same shape. The term was coined as a pun on animal reptiles by recreational mathematician Solomon W. Golomb and popularized by Martin Gardner in his "Mathematical Games" column in the May 1963 issue of Scientific American. In 2012 a generalization of rep-tiles called self-tiling tile sets was introduced by Lee Sallows in Mathematics Magazine.
A geometric magic square, often abbreviated to geomagic square, is a generalization of magic squares invented by Lee Sallows in 2001. A traditional magic square is a square array of numbers whose sum taken in any row, any column, or in either diagonal is the same target number. A geomagic square, on the other hand, is a square array of geometrical shapes in which those appearing in each row, column, or diagonal can be fitted together to create an identical shape called the target shape. As with numerical types, it is required that the entries in a geomagic square be distinct. Similarly, the eight trivial variants of any square resulting from its rotation and/or reflection are all counted as the same square. By the dimension of a geomagic square is meant the dimension of the pieces it uses. Hitherto interest has focused mainly on 2D squares using planar pieces, but pieces of any dimension are permitted.
A set of prototiles is aperiodic if copies of the prototiles can be assembled to create tilings, such that all possible tessellation patterns are non-periodic. The aperiodicity referred to is a property of the particular set of prototiles; the various resulting tilings themselves are just non-periodic.
A self-tiling tile set, or setiset, of order n is a set of n shapes or pieces, usually planar, each of which can be tiled with smaller replicas of the complete set of n shapes. That is, the n shapes can be assembled in n different ways so as to create larger copies of themselves, where the increase in scale is the same in each case. Figure 1 shows an example for n = 4 using distinctly shaped decominoes. The concept can be extended to include pieces of higher dimension. The name setisets was coined by Lee Sallows in 2012, but the problem of finding such sets for n = 4 was asked decades previously by C. Dudley Langford, and examples for polyaboloes and polyominoes were previously published by Gardner.
Royal Vale Heath was a wealthy New York stockbroker and writer who became widely known as a magician and puzzle enthusiast. His magic tricks were often based on mathematics and he introduced the term "mathemagic" to describe them in a 1933 book titled Mathemagic. He was a frequent contributor to Scripta Mathematica, Hugard's Magic Monthly, and The Jinx.
| Types |  | |
|---|---|---|
| Related shapes | ||
| Higher dimensional shapes | ||
| Classification | ||
| Related concepts | ||