In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form
In mathematics, the Baker–Campbell–Hausdorff formula is the solution for to the equation
Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions. Functional integrals arise in probability, in the study of partial differential equations, and in the path integral approach to the quantum mechanics of particles and fields.

In the physical sciences, the Airy function (or Airy function of the first kind) Ai(x) is a special function named after the British astronomer George Biddell Airy (1801–1892). The function Ai(x) and the related function Bi(x), are linearly independent solutions to the differential equation
In mathematics, the family of Debye functions is defined by

In mathematics, the exponential integral Ei is a special function on the complex plane.

The point spread function (PSF) describes the response of a focused optical imaging system to a point source or point object. A more general term for the PSF is the system's impulse response; the PSF is the impulse response or impulse response function (IRF) of a focused optical imaging system. The PSF in many contexts can be thought of as the extended blob in an image that represents a single point object, that is considered as a spatial impulse. In functional terms, it is the spatial domain version of the optical transfer function (OTF) of an imaging system. It is a useful concept in Fourier optics, astronomical imaging, medical imaging, electron microscopy and other imaging techniques such as 3D microscopy and fluorescence microscopy.

Tomographic reconstruction is a type of multidimensional inverse problem where the challenge is to yield an estimate of a specific system from a finite number of projections. The mathematical basis for tomographic imaging was laid down by Johann Radon. A notable example of applications is the reconstruction of computed tomography (CT) where cross-sectional images of patients are obtained in non-invasive manner. Recent developments have seen the Radon transform and its inverse used for tasks related to realistic object insertion required for testing and evaluating computed tomography use in airport security.
In mathematics, the Helmholtz equation is the eigenvalue problem for the Laplace operator. It corresponds to the linear partial differential equation

The Wigner quasiprobability distribution is a quasiprobability distribution. It was introduced by Eugene Wigner in 1932 to study quantum corrections to classical statistical mechanics. The goal was to link the wavefunction that appears in Schrödinger's equation to a probability distribution in phase space.
Rietveld refinement is a technique described by Hugo Rietveld for use in the characterisation of crystalline materials. The neutron and X-ray diffraction of powder samples results in a pattern characterised by reflections at certain positions. The height, width and position of these reflections can be used to determine many aspects of the material's structure.

In physics, physical optics, or wave optics, is the branch of optics that studies interference, diffraction, polarization, and other phenomena for which the ray approximation of geometric optics is not valid. This usage tends not to include effects such as quantum noise in optical communication, which is studied in the sub-branch of coherence theory.
In optics, the Fresnel diffraction equation for near-field diffraction is an approximation of the Kirchhoff–Fresnel diffraction that can be applied to the propagation of waves in the near field. It is used to calculate the diffraction pattern created by waves passing through an aperture or around an object, when viewed from relatively close to the object. In contrast the diffraction pattern in the far field region is given by the Fraunhofer diffraction equation.
In mathematics, the Fredholm determinant is a complex-valued function which generalizes the determinant of a finite dimensional linear operator. It is defined for bounded operators on a Hilbert space which differ from the identity operator by a trace-class operator. The function is named after the mathematician Erik Ivar Fredholm.

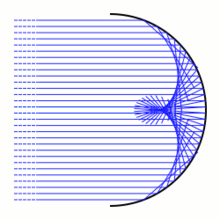
In optics, a caustic or caustic network is the envelope of light rays which have been reflected or refracted by a curved surface or object, or the projection of that envelope of rays on another surface. The caustic is a curve or surface to which each of the light rays is tangent, defining a boundary of an envelope of rays as a curve of concentrated light. Therefore, in the photo to the right, caustics can be seen as patches of light or their bright edges. These shapes often have cusp singularities.
The Sokhotski–Plemelj theorem is a theorem in complex analysis, which helps in evaluating certain integrals. The real-line version of it is often used in physics, although rarely referred to by name. The theorem is named after Julian Sochocki, who proved it in 1868, and Josip Plemelj, who rediscovered it as a main ingredient of his solution of the Riemann–Hilbert problem in 1908.
In numerical analysis Gauss–Laguerre quadrature is an extension of the Gaussian quadrature method for approximating the value of integrals of the following kind:

In numerical analysis, Gauss–Hermite quadrature is a form of Gaussian quadrature for approximating the value of integrals of the following kind:
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.