Perfect matching in high-degree hypergraphs

Last updated January 04, 2023

In graph theory, perfect matching in high-degree hypergraphs is a research avenue trying to find sufficient conditions for existence of a perfect matching in a hypergraph, based only on the degree of vertices or subsets of them.

Introduction

Degrees and matchings in graphs

In a simple graph $G = (V, E)$ , the degree of a vertex $v$ , often denoted by $deg(v)$ or $δ(v)$ , is the number of edges in $E$ adjacent to $v$ . The minimum degree of a graph, often denoted by $deg(G)$ or $δ(v)$ , is the minimum of $deg(v)$ over all vertices $v$ in $V$ .

A matching in a graph is a set of edges such that each vertex is adjacent to at most one edge; a perfect matching is a matching in which each vertex is adjacent to exactly one edge. A perfect matching does not always exist, and thus it is interesting to find sufficient conditions that guarantee its existence.

One such condition follows from Dirac's theorem on Hamiltonian cycles. It says that, if $deg(G) ≥ .mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}n⁄2$ , then the graph admits a Hamiltonian cycle; this implies that it admits a perfect matching. The factor $n ⁄ 2$ is tight, since the complete bipartite graph on $(n ⁄ 2 - 1, n ⁄ 2 + 1)$ vertices has degree $n ⁄ 2 - 1$ but does not admit a perfect matching.

The results described below aim to extend these results from graphs to hypergraphs.

Degrees in hypergraphs

In a hypergraph $H = (V, E)$ , each edge of $E$ may contain more than two vertices of $V$ . The degree of a vertex $v$ in $V$ is, as before, the number of edges in $E$ that contain $v$ . But in a hypergraph we can also consider the degree of subsets of vertices: given a subset $U$ of $V$ , $deg(U)$ is the number of edges in $E$ that contain all vertices of $U$ . Thus, the degree of a hypergraph can be defined in different ways depending on the size of subsets whose degree is considered.

Formally, for every integer $d \geq 1$ , $deg d (H)$ is the minimum of $deg(U)$ over all subsets $U$ of $V$ that contain exactly $d$ vertices. Thus, $deg 1 (H)$ corresponds to the definition of a degree of a simple graph, namely the smallest degree of a single vertex; $deg 2 (H)$ is the smallest degree of a pair of vertices; etc.

A hypergraph $H = (V, E)$ is called $r$ -uniform if every hyperedge in $E$ contains exactly $r$ vertices of $V$ . In $r$ -uniform graphs, the relevant values of $d$ are $1, 2, \dots , r - 1$ . In a simple graph, $r = 2$ .

Conditions on 1-vertex degree

Several authors proved sufficient conditions for the case $d = 1$ , i.e., conditions on the smallest degree of a single vertex.

If $H$ is a 3-uniform hypergraph on $n$ vertices, $n$ is a multiple of 3, and
$\deg _{1}(H)\geq {\bigg (}5/9+o(1){\bigg )}{n \choose 2},$
then $H$ contains a perfect matching.^[1]
If $H$ is a 3-uniform hypergraph on $n$ vertices, $n$ is a multiple of 3, and
$\deg _{1}(H)\geq {n-1 \choose 2}-{2n/3 \choose 2}+1,$
then $H$ contains a perfect matching - a matching of size $k$ . This result is the best possible.^[2]
If $H$ is a 4-uniform hypergraph with on $n$ vertices, $n$ is a multiple of 4, and
$\deg _{1}(H)\geq {n-1 \choose 3}-{3n/4 \choose 3},$
then $H$ contains a perfect matching - a matching of size $k$ . This result is the best possible.^[3]
If $H$ is $r$ -uniform, n is a multiple of $r$ , and
$\deg _{1}(H)>{\frac {r-1}{r}}\left({{\binom {n-1}{r-1}}-{\binom {n-kr-1}{r-1}}}\right),$
then $H$ contains a matching of size at least $k + 1$ . In particular, setting $k = n ⁄ r - 1$ gives that, if
$\deg _{1}(H)>{\frac {r-1}{r}}\left({{\binom {n-1}{r-1}}-1}\right),$
then $H$ contains a perfect matching.^[4]
If $H$ is $r$ -uniform and $r$ -partite, each side contains exactly $n$ vertices, and
$\deg _{1}(H)>{\frac {r-1}{r}}\left({n^{r-1}-(n-k)^{r-1}}\right),$
then $H$ contains a matching of size at least $k + 1$ . In particular, setting $k = n - 1$ gives that if
$\deg _{1}(H)>{\frac {r-1}{r}}\left({n^{r-1}-1}\right),$
then $H$ contains a perfect matching.^[4]

For comparison, Dirac's theorem on Hamiltonian cycles says that, if $H$ is 2-uniform (i.e., a simple graph) and

\deg _{1}(H)\geq {n-1 \choose 1}-{n/2 \choose 1}+1=n/2,

then $H$ admits a perfect matching.

Conditions on (r-1)-tuple degree

Several authors proved sufficient conditions for the case $d = r - 1$ , i.e., conditions on the smallest degree of sets of $r - 1$ vertices, in $r$ -uniform hypergraphs with $n$ vertices.

In r-partite r-uniform hypergraphs

The following results relate to $r$ -partite hypergraphs that have exactly $n$ vertices on each side ( $rn$ vertices overall):

If $\deg _{r-1}(H)\geq n/2+{\sqrt {2n\log _{2}n}}$
and $n \geq 1000$ , then $H$ has a perfect matching. This expression is smallest possible up to the lower-order term; in particular, $n ⁄ 2$ is not sufficient.^[5]
If $\deg _{r-1}(H)\geq n/r$
then $H$ admits a matching that covers all but at most $r - 2$ vertices in each vertex class of $H$ . The $n ⁄ r$ factor is essentially the best possible.^[5]
Let $V 1, \dots , V r$ be the $r$ sides of $H$ . If the degree of every $(r - 1)$ -tuple in $V ⁄ V 1$ is strictly larger than $n ⁄ 2$ , and the degree of every $(r - 1)$ -tuple in $V ⁄ V r$ is at least $n ⁄ 2$ , then $H$ admits a perfect matching. ^[6]

In general r-uniform hypergraphs

For every $γ > 0$ , when $n$ is large enough, if
$\deg _{r-1}(H)\geq (1/2+\gamma )n$
then $H$ is Hamiltonian, and thus contains a perfect matching.^[7]
If $\deg _{r-1}(H)\geq n/2+3r^{2}{\sqrt {n\log _{2}n}}$
and $n$ is sufficiently large, then $H$ admits a perfect matching.^[5]
If $\deg _{r-1}(H)\geq n/r+3r^{2}{\sqrt {n\log _{2}n}},$
then $H$ admits a matching that covers all but at most $2 r 2$ vertices. ^[5]
When n is divisible by r and sufficiently large, the threshold is
$\deg _{r-1}(H)\geq n/2-r+c_{k,n}$
where $c k, n$ is a constant depending on the parity of $n$ and $k$ (all expressions below are the best possible):^[8]
- 3 when $r ⁄ 2$ is even and $n ⁄ r$ is odd;
- 5⁄2 when $r$ is odd and $(n -1) ⁄ 2$ is odd;
- 3⁄2 when $r$ is odd and $(n -1) ⁄ 2$ is even;
- 2 otherwise.
When $n$ is not divisible by $r$ , the sufficient degree is close to $n ⁄ r$ : if $deg r -1 (H) \geq n ⁄ r + O (log(n))$ , then $H$ admits a perfect matching. The expression is almost the smallest possible: the smallest possible is $⌊ n ⁄ r ⌋$ .^[8]

Other conditions

There are some sufficient conditions for other values of $d$ :

For all $d \geq r ⁄ 2$ , the threshold for $deg d (H)$ is close to:^[9]
$\left({\frac {1}{2}}+o(1)\right){\binom {n}{r-d}}.$
For all $d < r ⁄ 2$ , the threshold for $deg d (H)$ is at most:^[1]
$\left({\frac {r-d}{r}}+o(1)\right){\binom {n-d}{r-d}}$
If $H$ is $r$ -partite and each side contains exactly $n$ vertices, and
$\deg _{d}(H)\geq {\frac {r-d}{r}}n^{r-d}+rn^{r-d-1},$
then $H$ contains a matching covering all but $(d - 1) r$ vertices.^[1]
If $n$ is sufficiently large and divisible by $r$ , and
$\deg _{d}(H)\geq {\frac {r-d}{r}}{\binom {n}{r-d}}+r^{r+1}(\ln {n})^{1/2}n^{r-d-1/2},$
then $H$ contains a matching covering all but $(d - 1) r$ vertices.^[1]

Related Research Articles

In graph theory, a perfect matching in a graph is a matching that covers every vertex of the graph. More formally, given a graph $G =$ , a perfect matching in $G$ is a subset $M$ of edge set $E$ , such that every vertex in the vertex set $V$ is adjacent to exactly one edge in $M$ .

In combinatorics, Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling of a sufficiently large complete graph. To demonstrate the theorem for two colours, let $r$ and $s$ be any two positive integers. Ramsey's theorem states that there exists a least positive integer $R (r, s)$ for which every blue-red edge colouring of the complete graph on $R (r, s)$ vertices contains a blue clique on $r$ vertices or a red clique on $s$ vertices.

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets $and, that is every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.$

In graph theory, Turán's theorem bounds the number of edges that can be included in an undirected graph that does not have a complete subgraph of a given size. It is one of the central results of extremal graph theory, an area studying the largest or smallest graphs with given properties, and is a special case of the forbidden subgraph problem on the maximum number of edges in a graph that does not have a given subgraph.

In graph theory, the degree of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex $is denoted or . The maximum degree of a graph, denoted by, and the minimum degree of a graph, denoted by, are the maximum and minimum of its vertices' degrees. In the multigraph shown on the right, the maximum degree is 5 and the minimum degree is 0.$

In graph theory, a graph is said to be a pseudorandom graph if it obeys certain properties that random graphs obey with high probability. There is no concrete definition of graph pseudorandomness, but there are many reasonable characterizations of pseudorandomness one can consider.

In extremal graph theory, the forbidden subgraph problem is the following problem: given a graph $, find the maximal number of edges an -vertex graph can have such that it does not have a subgraph isomorphic to . In this context, is called a forbidden subgraph .$

In mathematics, a packing in a hypergraph is a partition of the set of the hypergraph's edges into a number of disjoint subsets such that no pair of edges in each subset share any vertex. There are two famous algorithms to achieve asymptotically optimal packing in k-uniform hypergraphs. One of them is a random greedy algorithm which was proposed by Joel Spencer. He used a branching process to formally prove the optimal achievable bound under some side conditions. The other algorithm is called the Rödl nibble and was proposed by Vojtěch Rödl et al. They showed that the achievable packing by the Rödl nibble is in some sense close to that of the random greedy algorithm.

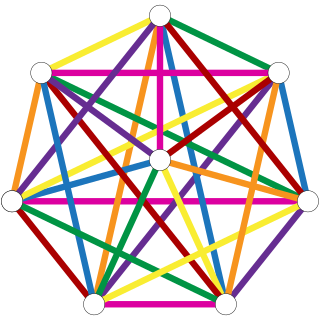
<span class="mw-page-title-main">Baranyai's theorem</span> Theorem that deals with the decompositions of complete hypergraphs

In combinatorial mathematics, Baranyai's theorem deals with the decompositions of complete hypergraphs.

In the mathematical discipline of graph theory, a rainbow matching in an edge-colored graph is a matching in which all the edges have distinct colors.

In mathematics, dependent random choice is a probabilistic technique that shows how to find a large set of vertices in a dense graph such that every small subset of vertices has many common neighbors. It is a useful tool to embed a graph into another graph with many edges. Thus it has its application in extremal graph theory, additive combinatorics and Ramsey theory.

In graph theory, a matching in a hypergraph is a set of hyperedges, in which every two hyperedges are disjoint. It is an extension of the notion of matching in a graph.

In graph theory, a vertex cover in a hypergraph is a set of vertices, such that every hyperedge of the hypergraph contains at least one vertex of that set. It is an extension of the notion of vertex cover in a graph.

In the mathematical field of graph theory, Hall-type theorems for hypergraphs are several generalizations of Hall's marriage theorem from graphs to hypergraphs. Such theorems were proved by Ofra Kessler, Ron Aharoni, Penny Haxell, Roy Meshulam, and others.

In graph theory, Ryser's conjecture is a conjecture relating the maximum matching size and the minimum transversal size in hypergraphs.

In geometry, a truncated projective plane (TPP), also known as a dual affine plane, is a special kind of a hypergraph or geometric configuration that is constructed in the following way.

In graph theory, Meshulam's game is a game used to explain a theorem of Roy Meshulam related to the homological connectivity of the independence complex of a graph, which is the smallest index k such that all reduced homological groups up to and including k are trivial. The formulation of this theorem as a game is due to Aharoni, Berger and Ziv.

In mathematics, the hypergraph regularity method is a powerful tool in extremal graph theory that refers to the combined application of the hypergraph regularity lemma and the associated counting lemma. It is a generalization of the graph regularity method, which refers to the use of Szemerédi's regularity and counting lemmas.

The blow-up lemma, proved by János Komlós, Gábor N. Sárközy, and Endre Szemerédi in 1997, is an important result in extremal graph theory, particularly within the context of the regularity method. It states that the regular pairs in the statement of Szemerédi's regularity lemma behave like complete bipartite graphs in the context of embedding spanning graphs of bounded degree.

The method of (hypergraph) containers is a powerful tool that can help characterize the typical structure and/or answer extremal questions about families of discrete objects with a prescribed set of local constraints. Such questions arise naturally in extremal graph theory, additive combinatorics, discrete geometry, coding theory, and Ramsey theory; they include some of the most classical problems in the associated fields.

References

1 2 3 4 Hàn, Hip; Person, Yury; Schacht, Mathias (2009-01-01). "On Perfect Matchings in Uniform Hypergraphs with Large Minimum Vertex Degree". SIAM Journal on Discrete Mathematics. 23 (2): 732–748. doi:10.1137/080729657. ISSN 0895-4801.
↑ Khan, Imdadullah (2013-01-01). "Perfect Matchings in 3-Uniform Hypergraphs with Large Vertex Degree". SIAM Journal on Discrete Mathematics. 27 (2): 1021–1039. doi:10.1137/10080796X. ISSN 0895-4801. S2CID 18434210.
↑ Khan, Imdadullah (2016-01-01). "Perfect matchings in 4-uniform hypergraphs". Journal of Combinatorial Theory, Series B. 116: 333–366. doi: 10.1016/j.jctb.2015.09.005 . ISSN 0095-8956.
1 2 Daykin, David E.; Häggkvist, Roland (1981-02-01). "Degrees giving independent edges in a hypergraph". Bulletin of the Australian Mathematical Society. 23 (1): 103–109. doi: 10.1017/S0004972700006924 . ISSN 1755-1633.
1 2 3 4 Kühn, Daniela; Osthus, Deryk (2006). "Matchings in hypergraphs of large minimum degree". Journal of Graph Theory. 51 (4): 269–280. doi:10.1002/jgt.20139. ISSN 1097-0118. S2CID 6769560.
↑ Aharoni, Ron; Georgakopoulos, Agelos; Sprüssel, Philipp (2009-01-01). "Perfect matchings in r-partite r-graphs". European Journal of Combinatorics. 30 (1): 39–42. arXiv: 0911.4008 . doi:10.1016/j.ejc.2008.02.011. ISSN 0195-6698. S2CID 1092170.
↑ Rödl, Vojtěch; Szemerédi, Endre; Ruciński, Andrzej (2008-03-01). "An approximate Dirac-type theorem for k-uniform hypergraphs". Combinatorica. 28 (2): 229–260. doi:10.1007/s00493-008-2295-z. ISSN 1439-6912. S2CID 5799411.
1 2 Rödl, Vojtech; Ruciński, Andrzej; Szemerédi, Endre (2009-04-01). "Perfect matchings in large uniform hypergraphs with large minimum collective degree". Journal of Combinatorial Theory, Series A. 116 (3): 613–636. doi: 10.1016/j.jcta.2008.10.002 . ISSN 0097-3165.
↑ Pikhurko, Oleg (2008-09-01). "Perfect Matchings and K 4 3 -Tilings in Hypergraphs of Large Codegree". Graphs and Combinatorics. 24 (4): 391–404. doi:10.1007/s00373-008-0787-7. ISSN 0911-0119. S2CID 29248979.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:3-1] 1 2 3 4 Hàn, Hip; Person, Yury; Schacht, Mathias (2009-01-01). "On Perfect Matchings in Uniform Hypergraphs with Large Minimum Vertex Degree". SIAM Journal on Discrete Mathematics. 23 (2): 732–748. doi:10.1137/080729657. ISSN 0895-4801.

[2] Khan, Imdadullah (2013-01-01). "Perfect Matchings in 3-Uniform Hypergraphs with Large Vertex Degree". SIAM Journal on Discrete Mathematics. 27 (2): 1021–1039. doi:10.1137/10080796X. ISSN 0895-4801. S2CID 18434210.

[3] Khan, Imdadullah (2016-01-01). "Perfect matchings in 4-uniform hypergraphs". Journal of Combinatorial Theory, Series B. 116: 333–366. doi: 10.1016/j.jctb.2015.09.005 . ISSN 0095-8956.

[:4-4] 1 2 Daykin, David E.; Häggkvist, Roland (1981-02-01). "Degrees giving independent edges in a hypergraph". Bulletin of the Australian Mathematical Society. 23 (1): 103–109. doi: 10.1017/S0004972700006924 . ISSN 1755-1633.

[:0-5] 1 2 3 4 Kühn, Daniela; Osthus, Deryk (2006). "Matchings in hypergraphs of large minimum degree". Journal of Graph Theory. 51 (4): 269–280. doi:10.1002/jgt.20139. ISSN 1097-0118. S2CID 6769560.

[6] Aharoni, Ron; Georgakopoulos, Agelos; Sprüssel, Philipp (2009-01-01). "Perfect matchings in r-partite r-graphs". European Journal of Combinatorics. 30 (1): 39–42. arXiv: 0911.4008 . doi:10.1016/j.ejc.2008.02.011. ISSN 0195-6698. S2CID 1092170.

[7] Rödl, Vojtěch; Szemerédi, Endre; Ruciński, Andrzej (2008-03-01). "An approximate Dirac-type theorem for k-uniform hypergraphs". Combinatorica. 28 (2): 229–260. doi:10.1007/s00493-008-2295-z. ISSN 1439-6912. S2CID 5799411.

[:1-8] 1 2 Rödl, Vojtech; Ruciński, Andrzej; Szemerédi, Endre (2009-04-01). "Perfect matchings in large uniform hypergraphs with large minimum collective degree". Journal of Combinatorial Theory, Series A. 116 (3): 613–636. doi: 10.1016/j.jcta.2008.10.002 . ISSN 0097-3165.

[:2-9] Pikhurko, Oleg (2008-09-01). "Perfect Matchings and K 4 3 -Tilings in Hypergraphs of Large Codegree". Graphs and Combinatorics. 24 (4): 391–404. doi:10.1007/s00373-008-0787-7. ISSN 0911-0119. S2CID 29248979.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]