In thermodynamics, the specific heat capacity of a substance is the heat capacity of a sample of the substance divided by the mass of the sample. Informally, it is the amount of energy that must be added, in the form of heat, to one unit of mass of the substance in order to cause an increase of one unit in temperature. The SI unit of specific heat is joule per kelvin and kilogram, J·kg−1·K−1. For example, the heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules so the specific heat capacity of water is 4184 J·kg−1·K−1.
In fluid dynamics, the Nusselt number (Nu) is the ratio of convective to conductive heat transfer at a boundary in a fluid. Convection includes both advection and diffusion (conduction). The conductive component is measured under the same conditions as the convective but for a hypothetically motionless fluid. It is a dimensionless number, closely related to the fluid's Rayleigh number.
The thermal conductivity of a material is a measure of its ability to conduct heat. It is commonly denoted by , , or .
Thermal conduction is the transfer of internal energy by microscopic collisions of particles and movement of electrons within a body. The colliding particles, which include molecules, atoms and electrons, transfer disorganized microscopic kinetic and potential energy, jointly known as internal energy. Conduction takes place in all phases: solid, liquid, and gas.
Newton's law of cooling states that the rate of heat loss of a body is directly proportional to the difference in the temperatures between the body and its surroundings. The law is frequently qualified to include the condition that the temperature difference is small and the nature of heat transfer mechanism remains the same. As such, it is equivalent to a statement that the heat transfer coefficient, which mediates between heat losses and temperature differences, is a constant. This condition is generally met in heat conduction as the thermal conductivity of most materials is only weakly dependent on temperature. In convective heat transfer, Newton's Law is followed for forced air or pumped fluid cooling, where the properties of the fluid do not vary strongly with temperature, but it is only approximately true for buoyancy-driven convection, where the velocity of the flow increases with temperature difference. Finally, in the case of heat transfer by thermal radiation, Newton's law of cooling holds only for very small temperature differences.

In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region.

In thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the useful work obtainable from a closed thermodynamic system at a constant temperature and volume. The negative of the change in the Helmholtz energy during a process is equal to the maximum amount of work that the system can perform in a thermodynamic process in which volume is held constant. If the volume were not held constant, part of this work would be performed as boundary work. This makes the Helmholtz energy useful for systems held at constant volume. Furthermore, at constant temperature, the Helmholtz free energy is minimized at equilibrium.

The lumped-element model simplifies the description of the behaviour of spatially distributed physical systems into a topology consisting of discrete entities that approximate the behaviour of the distributed system under certain assumptions. It is useful in electrical systems, mechanical multibody systems, heat transfer, acoustics, etc.

In classical statistical mechanics, the equipartition theorem relates the temperature of a system to its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium, energy is shared equally among all of its various forms; for example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion.
A heat current is a kinetic exchange rate between molecules, relative to the material in which the kinesis occurs. It is defined as , where is heat and is time.
The heat transfer coefficient or film coefficient, or film effectiveness, in thermodynamics and in mechanics is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat :

A dendrite in metallurgy is a characteristic tree-like structure of crystals growing as molten metal solidifies, the shape produced by faster growth along energetically favourable crystallographic directions. This dendritic growth has large consequences in regard to material properties.
In classical thermodynamics, entropy is a property of a thermodynamic system that expresses the direction or outcome of spontaneous changes in the system. The term was introduced by Rudolf Clausius in the mid-nineteenth century from the Greek word τρoπή (transformation) to explain the relationship of the internal energy that is available or unavailable for transformations in form of heat and work. Entropy predicts that certain processes are irreversible or impossible, despite not violating the conservation of energy. The definition of entropy is central to the establishment of the second law of thermodynamics, which states that the entropy of isolated systems cannot decrease with time, as they always tend to arrive at a state of thermodynamic equilibrium, where the entropy is highest. Entropy is therefore also considered to be a measure of disorder in the system.
In thermodynamics, the thermal effusivity, thermal inertia or thermal responsivity of a material is defined as the square root of the product of the material's thermal conductivity and its volumetric heat capacity.
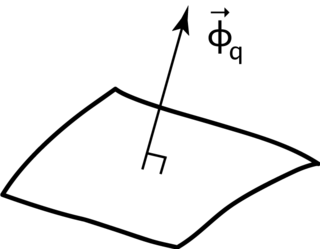
Heat flux or thermal flux, sometimes also referred to as heat flux density, heat-flow density or heat flow rate intensity is a flow of energy per unit of area per unit of time. In SI its units are watts per square metre (W/m2). It has both a direction and a magnitude, and so it is a vector quantity. To define the heat flux at a certain point in space, one takes the limiting case where the size of the surface becomes infinitesimally small.
Relativistic heat conduction refers to the modelling of heat conduction in a way compatible with special relativity. This article discusses models using a wave equation with a dissipative term.
Miniaturizing components has always been a primary goal in the semiconductor industry because it cuts production cost and lets companies build smaller computers and other devices. Miniaturization, however, has increased dissipated power per unit area and made it a key limiting factor in integrated circuit performance. Temperature increase becomes relevant for relatively small-cross-sections wires, where it may affect normal semiconductor behavior. Besides, since the generation of heat is proportional to the frequency of operation for switching circuits, fast computers have larger heat generation than slow ones, an undesired effect for chips manufacturers. This article summaries physical concepts that describe the generation and conduction of heat in an integrated circuit, and presents numerical methods that model heat transfer from a macroscopic point of view.
Interfacial thermal resistance, also known as thermal boundary resistance, or Kapitza resistance, is a measure of an interface's resistance to thermal flow. This thermal resistance differs from contact resistance because it exists even at atomically perfect interfaces. Owing to differences in electronic and vibrational properties in different materials, when an energy carrier attempts to traverse the interface, it will scatter at the interface. The probability of transmission after scattering will depend on the available energy states on side 1 and side 2 of the interface.
Phonons can scatter through several mechanisms as they travel through the material. These scattering mechanisms are: Umklapp phonon-phonon scattering, phonon-impurity scattering, phonon-electron scattering, and phonon-boundary scattering. Each scattering mechanism can be characterised by a relaxation rate 1/ which is the inverse of the corresponding relaxation time.
CFD stands for computational fluid dynamics. As per this technique, the governing differential equations of a flow system or thermal system are known in the form of Navier–Stokes equations, thermal energy equation and species equation with an appropriate equation of state. In the past few years, CFD has been playing an increasingly important role in building design, following its continuing development for over a quarter of a century. The information provided by CFD can be used to analyse the impact of building exhausts to the environment, to predict smoke and fire risks in buildings, to quantify indoor environment quality, and to design natural ventilation systems.














