Peter Littelmann (born 10 December 1957) is a German mathematician at the University of Cologne working on algebraic groups and representation theory, who introduced the Littelmann path model and used it to solve several conjectures in standard monomial theory and other areas.
Littelmann was an invited speaker at the International Congress of Mathematicians in Zürich (1994).
In mathematics, and more specifically in computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating set of an ideal in a polynomial ring K[x1, ..., xn] over a field K. A Gröbner basis allows many important properties of the ideal and the associated algebraic variety to be deduced easily, such as the dimension and the number of zeros when it is finite. Gröbner basis computation is one of the main practical tools for solving systems of polynomial equations and computing the images of algebraic varieties under projections or rational maps.
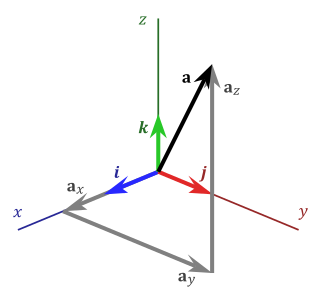
In mathematics, the standard basis (also called natural basis or canonical basis) of a coordinate vector space (such as or ) is the set of vectors, each of whose components are all zero, except one that equals 1. For example, in the case of the Euclidean plane formed by the pairs (x, y) of real numbers, the standard basis is formed by the vectors
Peter David Lax is a Hungarian-born American mathematician and Abel Prize laureate working in the areas of pure and applied mathematics.
In mathematics, more specifically in the theory of Lie algebras, the Poincaré–Birkhoff–Witt theorem is a result giving an explicit description of the universal enveloping algebra of a Lie algebra. It is named after Henri Poincaré, Garrett Birkhoff, and Ernst Witt.
Abū Bakr Muḥammad ibn al Ḥasan al-Karajī was a 10th-century Persian mathematician and engineer who flourished at Baghdad. He was born in Karaj, a city near Tehran. His three principal surviving works are mathematical: Al-Badi' fi'l-hisab, Al-Fakhri fi'l-jabr wa'l-muqabala, and Al-Kafi fi'l-hisab.
In mathematics, a (B, N) pair is a structure on groups of Lie type that allows one to give uniform proofs of many results, instead of giving a large number of case-by-case proofs. Roughly speaking, it shows that all such groups are similar to the general linear group over a field. They were introduced by the mathematician Jacques Tits, and are also sometimes known as Tits systems.
Conjeevaram Srirangachari SeshadriFRS was an Indian mathematician. He was the founder and director-emeritus of the Chennai Mathematical Institute, and is known for his work in algebraic geometry. The Seshadri constant is named after him. He was also known for his collaboration with mathematician M. S. Narasimhan, for their proof of the Narasimhan–Seshadri theorem which proved the necessary conditions for stable vector bundles on a Riemann surface.
James Alexander "Sandy" Green FRS was a mathematician and Professor at the Mathematics Institute at the University of Warwick, who worked in the field of representation theory.
In mathematics, the Littelmann path model is a combinatorial device due to Peter Littelmann for computing multiplicities without overcounting in the representation theory of symmetrisable Kac–Moody algebras. Its most important application is to complex semisimple Lie algebras or equivalently compact semisimple Lie groups, the case described in this article. Multiplicities in irreducible representations, tensor products and branching rules can be calculated using a coloured directed graph, with labels given by the simple roots of the Lie algebra.
Combinatorial commutative algebra is a relatively new, rapidly developing mathematical discipline. As the name implies, it lies at the intersection of two more established fields, commutative algebra and combinatorics, and frequently uses methods of one to address problems arising in the other. Less obviously, polyhedral geometry plays a significant role.
In ring theory, a branch of mathematics, a ring R is a polynomial identity ring if there is, for some N > 0, an element P ≠ 0 of the free algebra, Z⟨X1, X2, ..., XN⟩, over the ring of integers in N variables X1, X2, ..., XN such that
Ralph Saul Phillips was an American mathematician and academic known for his contributions to functional analysis, scattering theory, and servomechanisms. He served as a Professor of mathematics at Stanford University. He made major contributions to acoustical scattering theory in collaboration with Peter Lax, proving remarkable results on local energy decay and the connections between poles of the scattering matrix and the analytic properties of the resolvent. With Lax, he coauthored the widely referred book on scattering theory titled Scattering Theory for Automorphic Functions. Phillips received the 1997 Leroy P. Steele Prize for Lifetime Achievement.
Claudio Procesi is an Italian mathematician, known for works in algebra and representation theory.
In algebraic geometry, standard monomial theory describes the sections of a line bundle over a generalized flag variety or Schubert variety of a reductive algebraic group by giving an explicit basis of elements called standard monomials. Many of the results have been extended to Kac–Moody algebras and their groups.
Chitikila Musili was an Indian mathematician at the University of Hyderabad who developed standard monomial theory in collaboration with his PhD supervisor C. S. Seshadri.
In mathematics, the Demazure conjecture is a conjecture about representations of algebraic groups over the integers made by Demazure. The conjecture implies that many of the results of his paper can be extended from complex algebraic groups to algebraic groups over fields of other characteristics or over the integers. V. Lakshmibai, C. Musili, and C. S. Seshadri showed that Demazure's conjecture follows from their work on standard monomial theory, and Peter Littelmann extended this to all reductive algebraic groups.
In mathematical representation theory, a good filtration is a filtration of a representation of a reductive algebraic group G such that the subquotients are isomorphic to the spaces of sections F(λ) of line bundles λ over G/B for a Borel subgroup B. In characteristic 0 this is automatically true as the irreducible modules are all of the form F(λ), but this is not usually true in positive characteristic. Mathieu (1990) showed that the tensor product of two modules F(λ)⊗F(μ) has a good filtration, completing the results of Donkin (1985) who proved it in most cases and Wang (1982) who proved it in large characteristic. Littelmann (1992) showed that the existence of good filtrations for these tensor products also follows from standard monomial theory.
Marie A. Vitulli is an American mathematician and professor emerita at the University of Oregon.
Laura Anne Taalman, also known as mathgrrl, is an American mathematician known for her work on the mathematics of Sudoku and for her mathematical 3D printing models. Her mathematical research concerns knot theory and singular algebraic geometry; she is a professor of mathematics at James Madison University.
Patrizia M. Gianni is an Italian mathematician specializing in computer algebra. She is known for her early research on Gröbner bases including her discovery of the FGLM algorithm for changing monomial orderings in Gröbner bases, and for her development of the components of the Axiom computer algebra system concerning polynomials and rational functions.
| International | |
|---|---|
| National | |
| Academics | |
| Other | |
 | This article about a German mathematician is a stub. You can help Wikipedia by expanding it. |
