Related Research Articles

Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter. In particular it is concerned with the "condensed" phases that appear whenever the number of constituents in a system is extremely large and the interactions between the constituents are strong. The most familiar examples of condensed phases are solids and liquids, which arise from the electromagnetic forces between atoms. Condensed matter physicists seek to understand the behavior of these phases by using physical laws. In particular, they include the laws of quantum mechanics, electromagnetism and statistical mechanics.

Chaos theory is a branch of mathematics focusing on the study of chaos—states of dynamical systems whose apparently random states of disorder and irregularities are often governed by deterministic laws that are highly sensitive to initial conditions. Chaos theory is an interdisciplinary theory stating that, within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnectedness, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state. A metaphor for this behavior is that a butterfly flapping its wings in China can cause a hurricane in Texas.
The following outline is provided as an overview of and topical guide to chemistry:

Physics is the natural science that studies matter, its motion and behavior through space and time, and the related entities of energy and force. Physics is one of the most fundamental scientific disciplines, and its main goal is to understand how the universe behaves.
Physical science is a branch of natural science that studies non-living systems, in contrast to life science. It in turn has many branches, each referred to as a "physical science", together called the "physical sciences".
The following outline is provided as an overview of and topical guide to physics:

A theory of everything, final theory, ultimate theory, or master theory is a hypothetical single, all-encompassing, coherent theoretical framework of physics that fully explains and links together all physical aspects of the universe. Finding a TOE is one of the major unsolved problems in physics. String theory and M-theory have been proposed as theories of everything. Over the past few centuries, two theoretical frameworks have been developed that, together, most closely resemble a TOE. These two theories upon which all modern physics rests are general relativity and quantum mechanics. General relativity is a theoretical framework that only focuses on gravity for understanding the universe in regions of both large scale and high mass: stars, galaxies, clusters of galaxies, etc. On the other hand, quantum mechanics is a theoretical framework that only focuses on three non-gravitational forces for understanding the universe in regions of both small scale and low mass: sub-atomic particles, atoms, molecules, etc. Quantum mechanics successfully implemented the Standard Model that describes the three non-gravitational forces – strong nuclear, weak nuclear, and electromagnetic force – as well as all observed elementary particles.

In mathematics and physics, a soliton or solitary wave is a self-reinforcing wave packet that maintains its shape while it propagates at a constant velocity. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium. Solitons are the solutions of a widespread class of weakly nonlinear dispersive partial differential equations describing physical systems.

Computational physics is the study and implementation of numerical analysis to solve problems in physics for which a quantitative theory already exists. Historically, computational physics was the first application of modern computers in science, and is now a subset of computational science.
Multiphysics is defined as the coupled processes or systems involving more than one simultaneously occurring physical field and the studies of and knowledge about these processes and systems. As an interdisciplinary study area, multiphysics spans over many science and engineering disciplines. Multiphysics is a practice built on mathematics, physics, application, and numerical analysis. The mathematics involved usually contains partial differential equations and tensor analysis. The physics refers to common types of physical processes, e.g., heat transfer (thermo-), pore water movement (hydro-), concentration field, stress and strain (mechano-), dynamics (dyno-), chemical reactions, electrostatics (electro-), neutronics (neutro-), and magnetostatics (magneto-).

In physics, topological order is a kind of order in the zero-temperature phase of matter. Macroscopically, topological order is defined and described by robust ground state degeneracy and quantized non-Abelian geometric phases of degenerate ground states. Microscopically, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders cannot change into each other without a phase transition.

Louis Hirsch Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago. He is known for the introduction and development of the bracket polynomial and the Kauffman polynomial.
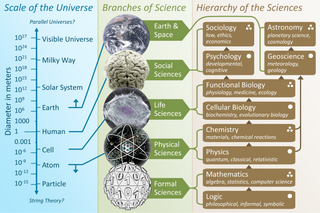
The branches of science, also referred to as sciences, "scientific fields", or "scientific disciplines," are commonly divided into three major groups:

Knots have been used for basic purposes such as recording information, fastening and tying objects together, for thousands of years. The early, significant stimulus in knot theory would arrive later with Sir William Thomson and his vortex theory of the atom.
Theoretical physics is a branch of physics that employs mathematical models and abstractions of physical objects and systems to rationalize, explain and predict natural phenomena. This is in contrast to experimental physics, which uses experimental tools to probe these phenomena.
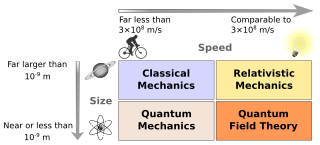
Physics deals with the combination of matter and energy. It also deals with a wide variety of systems, about which theories have been developed that are used by physicists. In general, theories are experimentally tested numerous times before they are accepted as correct as a description of Nature. For instance, the theory of classical mechanics accurately describes the motion of objects, provided they are much larger than atoms and moving at much less than the speed of light. These "central theories" are important tools for research in more specialized topics, and any physicist, regardless of his or her specialization, is expected to be literate in them.
The following outline is provided as an overview of and topical guide to natural science:
Topological ideas are relevant to fluid dynamics at the kinematic level, since any fluid flow involves continuous deformation of any transported scalar or vector field. Problems of stirring and mixing are particularly susceptible to topological techniques. Thus, for example, the Thurston–Nielsen classification has been fruitfully applied to the problem of stirring in two-dimensions by any number of stirrers following a time-periodic 'stirring protocol'. Other studies are concerned with flows having chaotic particle paths, and associated exponential rates of mixing.
Structural complexity is a science of applied mathematics, that aims at relating fundamental physical or biological aspects of a complex system with the mathematical description of the morphological complexity that the system exhibits, by establishing rigorous relations between mathematical and physical properties of such system.

Renzo Luigi Ricca is an Italian-born applied mathematician, professor of mathematical physics at the University of Milano-Bicocca. His principal research interests are in classical field theory, dynamical systems and structural complexity. He is known for his contributions to the field of geometric and topological fluid dynamics and, in particular, for his work on geometric and topological aspects of kinetic and magnetic helicity, and physical knot theory.
References
- Kauffman, L.H. (1991) Knots and Physics. Series on Knots and Everything 1, World Scientific.
- Kauffman, L.H., Editor (1991) Knots and Applications. Series on Knots and Everything 6, World Scientific.
- O’Hara, J. (2003) Energy of Knots and Conformal Geometry. Series on Knots and Everything 33, World Scientific.
- Ricca, R.L. (1998) Applications of knot theory in fluid mechanics. In Knot Theory (ed. V.F.R. Jones et al.), pp. 321–346. Banach Center Publs. 42, Polish Academy of Sciences, Warsaw.
| This Knot theory-related article is a stub. You can help Wikipedia by expanding it. |