The abundances of plant species are often measured by plant cover, which is the relative area covered by different plant species in a small plot. Plant cover is not biased by the size and distributions of individuals, and is an important and often measured characteristic of the composition of plant communities. [1] [2]
Plant cover data may be used to classify the studied plant community into a vegetation type, to test different ecological hypotheses on plant abundance, and in gradient studies, where the effects of different environmental gradients on the abundance of specific plant species are studied . [3]
The most common way to measure plant cover in herbal plant communities, is to make a visual assessment of the relative area covered by the different species in a small plot (see quadrat). The visually assessed cover of a plant species is then recorded as a continuous variable between 0 and 1, or divided into interval classes as an ordinal variable. [4] An alternative methodology, called the pin-point method (or point-intercept method), has also been widely employed.
In a pin-point analysis, a frame with a fixed grid pattern is placed randomly above the vegetation, and a thin pin is inserted vertically through one of the grid points into the vegetation. The different species touched by the pin are recorded at each insertion. The cover of plant species k in a plot, , is now assumed to be proportional to the number of “hits” by the pin,
,
where is the number of pins that hit species k out of a total of n pins. Since a single pin in multi-species plant communities often will hit more than a single species, the sum of the plant cover of the different species may be larger than unity when estimated by the pin-point method. The sum of the estimated plant cover is expected to increase with the number of plant species in a plot and with increasing 3-dimensional structuring of the plants in the community. Plant cover data obtained by the pin-point method may be modelled by a generalised binomial distribution (or Pólya–Eggenberger distribution). [5]
The method of least squares is a parameter estimation method in regression analysis based on minimizing the sum of the squares of the residuals made in the results of each individual equation.
In probability theory and statistics, the Zipf–Mandelbrot law is a discrete probability distribution. Also known as the Pareto–Zipf law, it is a power-law distribution on ranked data, named after the linguist George Kingsley Zipf, who suggested a simpler distribution called Zipf's law, and the mathematician Benoit Mandelbrot, who subsequently generalized it.
The unified neutral theory of biodiversity and biogeography is a theory and the title of a monograph by ecologist Stephen P. Hubbell. It aims to explain the diversity and relative abundance of species in ecological communities. Like other neutral theories of ecology, Hubbell assumes that the differences between members of an ecological community of trophically similar species are "neutral", or irrelevant to their success. This implies that niche differences do not influence abundance and the abundance of each species follows a random walk. The theory has sparked controversy, and some authors consider it a more complex version of other null models that fit the data better.
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to be a function of its predicted value.
In statistics, a mixture model is a probabilistic model for representing the presence of subpopulations within an overall population, without requiring that an observed data set should identify the sub-population to which an individual observation belongs. Formally a mixture model corresponds to the mixture distribution that represents the probability distribution of observations in the overall population. However, while problems associated with "mixture distributions" relate to deriving the properties of the overall population from those of the sub-populations, "mixture models" are used to make statistical inferences about the properties of the sub-populations given only observations on the pooled population, without sub-population identity information. Mixture models are used for clustering, under the name model-based clustering, and also for density estimation.
Spatial ecology studies the ultimate distributional or spatial unit occupied by a species. In a particular habitat shared by several species, each of the species is usually confined to its own microhabitat or spatial niche because two species in the same general territory cannot usually occupy the same ecological niche for any significant length of time.
The species–area relationship or species–area curve describes the relationship between the area of a habitat, or of part of a habitat, and the number of species found within that area. Larger areas tend to contain larger numbers of species, and empirically, the relative numbers seem to follow systematic mathematical relationships. The species–area relationship is usually constructed for a single type of organism, such as all vascular plants or all species of a specific trophic level within a particular site. It is rarely if ever, constructed for all types of organisms if simply because of the prodigious data requirements. It is related but not identical to the species discovery curve.
A paleothermometer is a methodology that provides an estimate of the ambient temperature at the time of formation of a natural material. Most paleothermometers are based on empirically-calibrated proxy relationships, such as the tree ring or TEX86 methods. Isotope methods, such as the δ18O method or the clumped-isotope method, are able to provide, at least in theory, direct measurements of temperature.
In statistics, Poisson regression is a generalized linear model form of regression analysis used to model count data and contingency tables. Poisson regression assumes the response variable Y has a Poisson distribution, and assumes the logarithm of its expected value can be modeled by a linear combination of unknown parameters. A Poisson regression model is sometimes known as a log-linear model, especially when used to model contingency tables.
In statistics, binomial regression is a regression analysis technique in which the response has a binomial distribution: it is the number of successes in a series of independent Bernoulli trials, where each trial has probability of success . In binomial regression, the probability of a success is related to explanatory variables: the corresponding concept in ordinary regression is to relate the mean value of the unobserved response to explanatory variables.
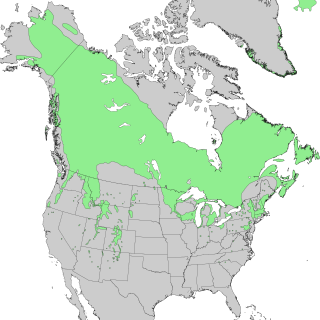
Species distribution, or speciesdispersion, is the manner in which a biological taxon is spatially arranged. The geographic limits of a particular taxon's distribution is its range, often represented as shaded areas on a map. Patterns of distribution change depending on the scale at which they are viewed, from the arrangement of individuals within a small family unit, to patterns within a population, or the distribution of the entire species as a whole (range). Species distribution is not to be confused with dispersal, which is the movement of individuals away from their region of origin or from a population center of high density.
In ecology, local abundance is the relative representation of a species in a particular ecosystem. It is usually measured as the number of individuals found per sample. The ratio of abundance of one species to one or multiple other species living in an ecosystem is referred to as relative species abundances. Both indicators are relevant for computing biodiversity.
In spatial ecology and macroecology, scaling pattern of occupancy (SPO), also known as the area-of-occupancy (AOO) is the way in which species distribution changes across spatial scales. In physical geography and image analysis, it is similar to the modifiable areal unit problem. Simon A. Levin (1992) states that the problem of relating phenomena across scales is the central problem in biology and in all of science. Understanding the SPO is thus one central theme in ecology.
In computer science, online machine learning is a method of machine learning in which data becomes available in a sequential order and is used to update the best predictor for future data at each step, as opposed to batch learning techniques which generate the best predictor by learning on the entire training data set at once. Online learning is a common technique used in areas of machine learning where it is computationally infeasible to train over the entire dataset, requiring the need of out-of-core algorithms. It is also used in situations where it is necessary for the algorithm to dynamically adapt to new patterns in the data, or when the data itself is generated as a function of time, e.g., stock price prediction. Online learning algorithms may be prone to catastrophic interference, a problem that can be addressed by incremental learning approaches.
Mechanistic models for niche apportionment are biological models used to explain relative species abundance distributions. These niche apportionment models describe how species break up resource pool in multi-dimensional space, determining the distribution of abundances of individuals among species. The relative abundances of species are usually expressed as a Whittaker plot, or rank abundance plot, where species are ranked by number of individuals on the x-axis, plotted against the log relative abundance of each species on the y-axis. The relative abundance can be measured as the relative number of individuals within species or the relative biomass of individuals within species.
Relative species abundance is a component of biodiversity and is a measure of how common or rare a species is relative to other species in a defined location or community. Relative abundance is the percent composition of an organism of a particular kind relative to the total number of organisms in the area. Relative species abundances tend to conform to specific patterns that are among the best-known and most-studied patterns in macroecology. Different populations in a community exist in relative proportions; this idea is known as relative abundance.
The generalized Lotka–Volterra equations are a set of equations which are more general than either the competitive or predator–prey examples of Lotka–Volterra types. They can be used to model direct competition and trophic relationships between an arbitrary number of species. Their dynamics can be analysed analytically to some extent. This makes them useful as a theoretical tool for modeling food webs. However, they lack features of other ecological models such as predator preference and nonlinear functional responses, and they cannot be used to model mutualism without allowing indefinite population growth.
Species distribution modelling (SDM), also known as environmental(or ecological) niche modelling (ENM), habitat modelling, predictive habitat distribution modelling, and range mapping uses ecological models to predict the distribution of a species across geographic space and time using environmental data. The environmental data are most often climate data (e.g. temperature, precipitation), but can include other variables such as soil type, water depth, and land cover. SDMs are used in several research areas in conservation biology, ecology and evolution. These models can be used to understand how environmental conditions influence the occurrence or abundance of a species, and for predictive purposes (ecological forecasting). Predictions from an SDM may be of a species’ future distribution under climate change, a species’ past distribution in order to assess evolutionary relationships, or the potential future distribution of an invasive species. Predictions of current and/or future habitat suitability can be useful for management applications (e.g. reintroduction or translocation of vulnerable species, reserve placement in anticipation of climate change).
Taylor's power law is an empirical law in ecology that relates the variance of the number of individuals of a species per unit area of habitat to the corresponding mean by a power law relationship. It is named after the ecologist who first proposed it in 1961, Lionel Roy Taylor (1924–2007). Taylor's original name for this relationship was the law of the mean. The name Taylor's law was coined by Southwood in 1966.
In statistics, the class of vector generalized linear models (VGLMs) was proposed to enlarge the scope of models catered for by generalized linear models (GLMs). In particular, VGLMs allow for response variables outside the classical exponential family and for more than one parameter. Each parameter can be transformed by a link function. The VGLM framework is also large enough to naturally accommodate multiple responses; these are several independent responses each coming from a particular statistical distribution with possibly different parameter values.
