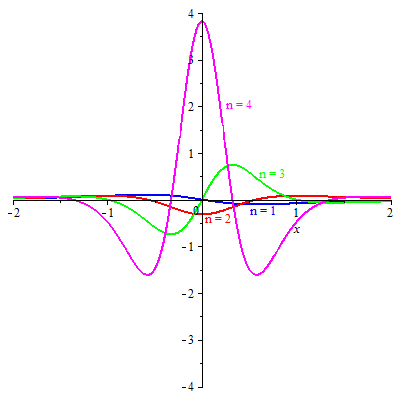
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary smooth potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
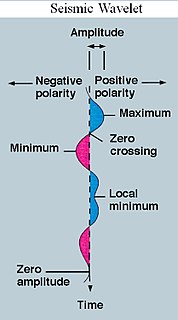
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one recorded by a seismograph or heart monitor. Generally, wavelets are intentionally crafted to have specific properties that make them useful for signal processing.

In mathematics, a Fourier transform (FT) is a mathematical transform that decomposes functions depending on space or time into functions depending on spatial or temporal frequency, such as the expression of a musical chord in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time.

The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.
In mathematics and in signal processing, the Hilbert transform is a specific linear operator that takes a function, u(t) of a real variable and produces another function of a real variable H(u)(t). This linear operator is given by convolution with the function . The Hilbert transform has a particularly simple representation in the frequency domain: It imparts a phase shift of ±90° to every frequency component of a function, the sign of the shift depending on the sign of the frequency. The Hilbert transform is important in signal processing, where it is a component of the analytic representation of a real-valued signal u(t). The Hilbert transform was first introduced by David Hilbert in this setting, to solve a special case of the Riemann–Hilbert problem for analytic functions.

In mathematics, the continuous wavelet transform (CWT) is a formal tool that provides an overcomplete representation of a signal by letting the translation and scale parameter of the wavelets vary continuously.

In physics, canonical quantization is a procedure for quantizing a classical theory, while attempting to preserve the formal structure, such as symmetries, of the classical theory, to the greatest extent possible.
In mathematics, the Lerch zeta function, sometimes called the Hurwitz–Lerch zeta function, is a special function that generalizes the Hurwitz zeta function and the polylogarithm. It is named after the Czech mathematician Mathias Lerch.
In mathematical physics, some approaches to quantum field theory are more popular than others. For historical reasons, the Schrödinger representation is less favored than Fock space methods. In the early days of quantum field theory, maintaining symmetries such as Lorentz invariance, displaying them manifestly, and proving renormalisation were of paramount importance. The Schrödinger representation is not manifestly Lorentz invariant and its renormalisability was only shown as recently as the 1980s by Kurt Symanzik (1981).
Continuous wavelets of compact support can be built, which are related to the beta distribution. The process is derived from probability distributions using blur derivative. These new wavelets have just one cycle, so they are termed unicycle wavelets. They can be viewed as a soft variety of Haar wavelets whose shape is fine-tuned by two parameters and . Closed-form expressions for beta wavelets and scale functions as well as their spectra are derived. Their importance is due to the Central Limit Theorem by Gnedenko and Kolmogorov applied for compactly supported signals.
In the mathematical topic of wavelet theory, the cascade algorithm is a numerical method for calculating function values of the basic scaling and wavelet functions of a discrete wavelet transform using an iterative algorithm. It starts from values on a coarse sequence of sampling points and produces values for successively more densely spaced sequences of sampling points. Because it applies the same operation over and over to the output of the previous application, it is known as the cascade algorithm.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
An LC circuit can be quantized using the same methods as for the quantum harmonic oscillator. An LC circuit is a variety of resonant circuit, and consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C. When connected together, an electric current can alternate between them at the circuit's resonant frequency:
Filtering in the context of large eddy simulation (LES) is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations. Because the principal difficulty in simulating turbulent flows comes from the wide range of length and time scales, this operation makes turbulent flow simulation cheaper by reducing the range of scales that must be resolved. The LES filter operation is low-pass, meaning it filters out the scales associated with high frequencies.
Coherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the article Coherent states. However, they have generated a huge variety of generalizations, which have led to a tremendous amount of literature in mathematical physics. In this article, we sketch the main directions of research on this line. For further details, we refer to several existing surveys.
Fractional wavelet transform (FRWT) is a generalization of the classical wavelet transform (WT). This transform is proposed in order to rectify the limitations of the WT and the fractional Fourier transform (FRFT). The FRWT inherits the advantages of multiresolution analysis of the WT and has the capability of signal representations in the fractional domain which is similar to the FRFT.
In mathematics, the Neumann–Poincaré operator or Poincaré–Neumann operator, named after Carl Neumann and Henri Poincaré, is a non-self-adjoint compact operator introduced by Poincaré to solve boundary value problems for the Laplacian on bounded domains in Euclidean space. Within the language of potential theory it reduces the partial differential equation to an integral equation on the boundary to which the theory of Fredholm operators can be applied. The theory is particularly simple in two dimensions—the case treated in detail in this article—where it is related to complex function theory, the conjugate Beurling transform or complex Hilbert transform and the Fredholm eigenvalues of bounded planar domains.
In probability theory, a branch of mathematics, white noise analysis, otherwise known as Hida calculus, is a framework for infinite-dimensional and stochastic calculus, based on the Gaussian white noise probability space, to be compared with Malliavin calculus based on the Wiener process. It was initiated by Takeyuki Hida in his 1975 Carleton Mathematical Lecture Notes.
Phase reduction is a method used to reduce a multi-dimensional dynamical equation describing a nonlinear limit cycle oscillator into a one-dimensional phase equation. Many phenomena in our world such as chemical reactions, electric circuits, mechanical vibrations, cardiac cells, and spiking neurons are examples of rhythmic phenomena, and can be considered as nonlinear limit cycle oscillators.
In functional analysis, every C*-algebra is isomorphic to a subalgebra of the C*-algebra of bounded linear operators on some Hilbert space H. This article describes the spectral theory of closed normal subalgebras of