
In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.

In mathematics, a 3-sphere, glome or hypersphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.

In physics and mathematics, the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical and quantum setting for all (non-gravitational) physical phenomena. The Lorentz group is named for the Dutch physicist Hendrik Lorentz.
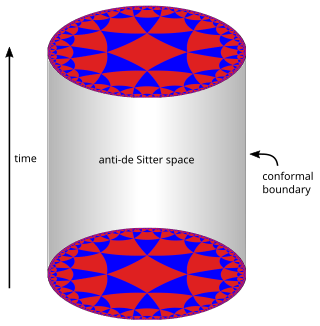
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have a sign (as in the sign of an angle): a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane, denoted below as H, together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry.
In mathematics, the Schwarzian derivative is an operator similar to the derivative which is invariant under Möbius transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and hypergeometric functions. It plays an important role in the theory of univalent functions, conformal mapping and Teichmüller spaces. It is named after the German mathematician Hermann Schwarz.
In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix
In mathematics, the Cayley transform, named after Arthur Cayley, is any of a cluster of related things. As originally described by Cayley (1846), the Cayley transform is a mapping between skew-symmetric matrices and special orthogonal matrices. The transform is a homography used in real analysis, complex analysis, and quaternionic analysis. In the theory of Hilbert spaces, the Cayley transform is a mapping between linear operators.
In mathematics, a Killing vector field, named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold. More simply, the flow generates a symmetry, in the sense that moving each point of an object the same distance in the direction of the Killing vector will not distort distances on the object.
In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program. The idea of reducing geometry to its characteristic group was developed particularly by Mario Pieri in his reduction of the primitive notions of geometry to merely point and motion.
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.
In mathematics, a fundamental polygon can be defined for every compact Riemann surface of genus greater than 0. It encodes not only the topology of the surface through its fundamental group but also determines the Riemann surface up to conformal equivalence. By the uniformization theorem, every compact Riemann surface has simply connected universal covering surface given by exactly one of the following:

In geometry, a Schwarz triangle, named after Hermann Schwarz, is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in Schwarz (1873).
In mathematics, a local system on a topological space X is a tool from algebraic topology which interpolates between cohomology with coefficients in a fixed abelian group A, and general sheaf cohomology in which coefficients vary from point to point. Local coefficient systems were introduced by Norman Steenrod in 1943.
In mathematics, the theta representation is a particular representation of the Heisenberg group of quantum mechanics. It gains its name from the fact that the Jacobi theta function is invariant under the action of a discrete subgroup of the Heisenberg group. The representation was popularized by David Mumford.
The history of Lorentz transformations comprises the development of linear transformations forming the Lorentz group or Poincaré group preserving the Lorentz interval and the Minkowski inner product .

In mathematics, a Scherk surface is an example of a minimal surface. Scherk described two complete embedded minimal surfaces in 1834; his first surface is a doubly periodic surface, his second surface is singly periodic. They were the third non-trivial examples of minimal surfaces. The two surfaces are conjugates of each other.
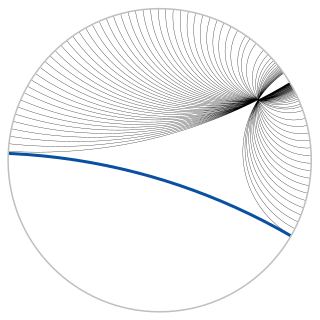
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk that are orthogonal to the unit circle or diameters of the unit circle.
In the hyperbolic plane, as in the Euclidean plane, each point can be uniquely identified by two real numbers. Several qualitatively different ways of coordinatizing the plane in hyperbolic geometry are used.



















































