Polynomial-time reduction

Last updated June 07, 2023

In computational complexity theory, a polynomial-time reduction is a method for solving one problem using another. One shows that if a hypothetical subroutine solving the second problem exists, then the first problem can be solved by transforming or reducing it to inputs for the second problem and calling the subroutine one or more times. If both the time required to transform the first problem to the second, and the number of times the subroutine is called is polynomial, then the first problem is polynomial-time reducible to the second.^[1]

A polynomial-time reduction proves that the first problem is no more difficult than the second one, because whenever an efficient algorithm exists for the second problem, one exists for the first problem as well. By contraposition, if no efficient algorithm exists for the first problem, none exists for the second either.^[1] Polynomial-time reductions are frequently used in complexity theory for defining both complexity classes and complete problems for those classes.

Types of reductions

The three most common types of polynomial-time reduction, from the most to the least restrictive, are polynomial-time many-one reductions, truth-table reductions, and Turing reductions. The most frequently used of these are the many-one reductions, and in some cases the phrase "polynomial-time reduction" may be used to mean a polynomial-time many-one reduction.^[2] The most general reductions are the Turing reductions and the most restrictive are the many-one reductions with truth-table reductions occupying the space in between.^[3]

Many-one reductions

A polynomial-time many-one reduction from a problem A to a problem B (both of which are usually required to be decision problems) is a polynomial-time algorithm for transforming inputs to problem A into inputs to problem B, such that the transformed problem has the same output as the original problem. An instance x of problem A can be solved by applying this transformation to produce an instance y of problem B, giving y as the input to an algorithm for problem B, and returning its output. Polynomial-time many-one reductions may also be known as polynomial transformations or Karp reductions, named after Richard Karp. A reduction of this type is denoted by $A\leq _{m}^{P}B$ or $A\leq _{p}B$ .^[4]^[1]

Truth-table reductions

A polynomial-time truth-table reduction from a problem A to a problem B (both decision problems) is a polynomial time algorithm for transforming inputs to problem A into a fixed number of inputs to problem B, such that the output for the original problem can be expressed as a function of the outputs for B. The function that maps outputs for B into the output for A must be the same for all inputs, so that it can be expressed by a truth table. A reduction of this type may be denoted by the expression $A\leq _{tt}^{P}B$ .^[5]

Turing reductions

A polynomial-time Turing reduction from a problem A to a problem B is an algorithm that solves problem A using a polynomial number of calls to a subroutine for problem B, and polynomial time outside of those subroutine calls. Polynomial-time Turing reductions are also known as Cook reductions, named after Stephen Cook. A reduction of this type may be denoted by the expression $A\leq _{T}^{P}B$ .^[4] Many-one reductions can be regarded as restricted variants of Turing reductions where the number of calls made to the subroutine for problem B is exactly one and the value returned by the reduction is the same value as the one returned by the subroutine.

Completeness

A complete problem for a given complexity class C and reduction ≤ is a problem P that belongs to C, such that every problem A in C has a reduction A ≤ P. For instance, a problem is NP-complete if it belongs to NP and all problems in NP have polynomial-time many-one reductions to it. A problem that belongs to NP can be proven to be NP-complete by finding a single polynomial-time many-one reduction to it from a known NP-complete problem.^[6] Polynomial-time many-one reductions have been used to define complete problems for other complexity classes, including the PSPACE-complete languages and EXPTIME-complete languages.^[7]

Every decision problem in P (the class of polynomial-time decision problems) may be reduced to every other nontrivial decision problem (where nontrivial means that not every input has the same output), by a polynomial-time many-one reduction. To transform an instance of problem A to B, solve A in polynomial time, and then use the solution to choose one of two instances of problem B with different answers. Therefore, for complexity classes within P such as L, NL, NC, and P itself, polynomial-time reductions cannot be used to define complete languages: if they were used in this way, every nontrivial problem in P would be complete. Instead, weaker reductions such as log-space reductions or NC reductions are used for defining classes of complete problems for these classes, such as the P-complete problems.^[8]

Defining complexity classes

The definitions of the complexity classes NP, PSPACE, and EXPTIME do not involve reductions: reductions come into their study only in the definition of complete languages for these classes. However, in some cases a complexity class may be defined by reductions. If C is any decision problem, then one can define a complexity class C consisting of the languages A for which $A\leq _{m}^{P}C$ . In this case, C will automatically be complete for C, but C may have other complete problems as well.

An example of this is the complexity class $\exists \mathbb {R}$ defined from the existential theory of the reals, a computational problem that is known to be NP-hard and in PSPACE , but is not known to be complete for NP, PSPACE, or any language in the polynomial hierarchy. $\exists \mathbb {R}$ is the set of problems having a polynomial-time many-one reduction to the existential theory of the reals; it has several other complete problems such as determining the rectilinear crossing number of an undirected graph. Each problem in $\exists \mathbb {R}$ inherits the property of belonging to PSPACE, and each $\exists \mathbb {R}$ -complete problem is NP-hard.^[9]

Similarly, the complexity class GI consists of the problems that can be reduced to the graph isomorphism problem. Since graph isomorphism is known to belong both to NP and co-AM, the same is true for every problem in this class. A problem is GI-complete if it is complete for this class; the graph isomorphism problem itself is GI-complete, as are several other related problems.^[10]

External links

MIT OpenCourseWare: 16. Complexity: P, NP, NP-completeness, Reductions

Related Research Articles

The P versus NP problem is a major unsolved problem in theoretical computer science. In informal terms, it asks whether every problem whose solution can be quickly verified can also be quickly solved.

In computational complexity theory, co-NP is a complexity class. A decision problem X is a member of co-NP if and only if its complement X is in the complexity class NP. The class can be defined as follows: a decision problem is in co-NP precisely if only no-instances have a polynomial-length "certificate" and there is a polynomial-time algorithm that can be used to verify any purported certificate.

In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and relating these classes to each other. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

In computational complexity theory, NP is a complexity class used to classify decision problems. NP is the set of decision problems for which the problem instances, where the answer is "yes", have proofs verifiable in polynomial time by a deterministic Turing machine, or alternatively the set of problems that can be solved in polynomial time by a nondeterministic Turing machine.

The #P-complete problems form a complexity class in computational complexity theory. The problems in this complexity class are defined by having the following two properties:

<span class="mw-page-title-main">PSPACE</span> Set of decision problems

In computational complexity theory, PSPACE is the set of all decision problems that can be solved by a Turing machine using a polynomial amount of space.

In computational complexity theory, NP-hardness is the defining property of a class of problems that are informally "at least as hard as the hardest problems in NP". A simple example of an NP-hard problem is the subset sum problem.

In computational complexity theory, a decision problem is P-complete if it is in P and every problem in P can be reduced to it by an appropriate reduction.

In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input length and if every other problem that can be solved in polynomial space can be transformed to it in polynomial time. The problems that are PSPACE-complete can be thought of as the hardest problems in PSPACE, the class of decision problems solvable in polynomial space, because a solution to any one such problem could easily be used to solve any other problem in PSPACE.

In computational complexity theory, the complexity class EXPTIME (sometimes called EXP or DEXPTIME) is the set of all decision problems that are solvable by a deterministic Turing machine in exponential time, i.e., in O(2^p(n)) time, where p(n) is a polynomial function of n.

In computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem to another decision problem using an effective function. The reduced instance is in the language $if and only if the initial instance is in its language . Thus if we can decide whether instances are in the language, we can decide whether instances are in its language by applying the reduction and solving . Thus, reductions can be used to measure the relative computational difficulty of two problems. It is said that reduces to if, in layman's terms is harder to solve than . That is to say, any algorithm that solves can also be used as part of a program that solves .$

In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor.

In computational complexity theory, a complexity class is a set of computational problems of related resource-based complexity. The two most commonly analyzed resources are time and memory.

In computer science, parameterized complexity is a branch of computational complexity theory that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input or output. The complexity of a problem is then measured as a function of those parameters. This allows the classification of NP-hard problems on a finer scale than in the classical setting, where the complexity of a problem is only measured as a function of the number of bits in the input. This appears to have been first demonstrated in Gurevich, Stockmeyer & Vishkin (1984). The first systematic work on parameterized complexity was done by Downey & Fellows (1999).

In computational complexity theory, P, also known as PTIME or DTIME(n^O(1)), is a fundamental complexity class. It contains all decision problems that can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.

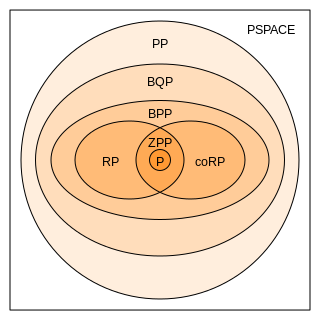
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time. The complexity class was defined by Gill in 1977.

In computational complexity theory, the Cook–Levin theorem, also known as Cook's theorem, states that the Boolean satisfiability problem is NP-complete. That is, it is in NP, and any problem in NP can be reduced in polynomial time by a deterministic Turing machine to the Boolean satisfiability problem.

In computational complexity theory, the complexity class NEXPTIME is the set of decision problems that can be solved by a non-deterministic Turing machine using time $.$

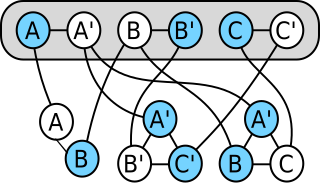
In computability theory and computational complexity theory, a reduction is an algorithm for transforming one problem into another problem. A sufficiently efficient reduction from one problem to another may be used to show that the second problem is at least as difficult as the first.

In computational complexity theory, a problem is NP-complete when:

It is a decision problem, meaning that for any input to the problem, the output is either "yes" or "no".
When the answer is "yes", this can be demonstrated through the existence of a short solution.
The correctness of each solution can be verified quickly and a brute-force search algorithm can find a solution by trying all possible solutions.
The problem can be used to simulate every other problem for which we can verify quickly that a solution is correct. In this sense, NP-complete problems are the hardest of the problems to which solutions can be verified quickly. If we could find solutions of some NP-complete problem quickly, we could quickly find the solutions of every other problem to which a given solution can be easily verified.

References

1 2 3 Kleinberg, Jon; Tardos, Éva (2006). Algorithm Design. Pearson Education. pp. 452–453. ISBN 978-0-321-37291-8.
↑ Wegener, Ingo (2005), Complexity Theory: Exploring the Limits of Efficient Algorithms, Springer, p. 60, ISBN 9783540274773 .
↑ Mandal, Debasis; Pavan, A.; Venugopalan, Rajeswari (2014). Separating Cook Completeness from Karp-Levin Completeness under a Worst-Case Hardness Hypothesis. 34th International Conference on Foundation of Software Technology and Theoretical Computer Science. ISBN 978-3-939897-77-4.
1 2 Goldreich, Oded (2008), Computational Complexity: A Conceptual Perspective, Cambridge University Press, pp. 59–60, ISBN 9781139472746
↑ Buss, S.R.; Hay, L. (1988), "On truth-table reducibility to SAT and the difference hierarchy over NP", Proceedings of Third Annual Structure in Complexity Theory Conference, pp. 224–233, CiteSeerX 10.1.1.5.2387 , doi:10.1109/SCT.1988.5282, ISBN 978-0-8186-0866-7 .
↑ Garey, Michael R.; Johnson, D. S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman.
↑ Aho, A. V. (2011), "Complexity theory", in Blum, E. K.; Aho, A. V. (eds.), Computer Science: The Hardware, Software and Heart of It, pp. 241–267, doi: 10.1007/978-1-4614-1168-0_12 , ISBN 978-1-4614-1167-3 . See in particular p. 255.
↑ Greenlaw, Raymond; Hoover, James; Ruzzo, Walter (1995), Limits To Parallel computation; P-Completeness Theory, ISBN 978-0-19-508591-4 . In particular, for the argument that every nontrivial problem in P has a polynomial-time many-one reduction to every other nontrivial problem, see p. 48.
↑ Schaefer, Marcus (2010), "Complexity of some geometric and topological problems" (PDF), Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers, Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 334–344, doi: 10.1007/978-3-642-11805-0_32 , ISBN 978-3-642-11804-3 .
↑ Köbler, Johannes; Schöning, Uwe; Torán, Jacobo (1993), The Graph Isomorphism Problem: Its Structural Complexity, Birkhäuser, ISBN 978-0-8176-3680-7, OCLC 246882287 .

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[kleinberg-tardos-1] 1 2 3 Kleinberg, Jon; Tardos, Éva (2006). Algorithm Design. Pearson Education. pp. 452–453. ISBN 978-0-321-37291-8.

[2] Wegener, Ingo (2005), Complexity Theory: Exploring the Limits of Efficient Algorithms, Springer, p. 60, ISBN 9783540274773 .

[mandal2014-3] Mandal, Debasis; Pavan, A.; Venugopalan, Rajeswari (2014). Separating Cook Completeness from Karp-Levin Completeness under a Worst-Case Hardness Hypothesis. 34th International Conference on Foundation of Software Technology and Theoretical Computer Science. ISBN 978-3-939897-77-4.

[goldreich-4] 1 2 Goldreich, Oded (2008), Computational Complexity: A Conceptual Perspective, Cambridge University Press, pp. 59–60, ISBN 9781139472746

[5] Buss, S.R.; Hay, L. (1988), "On truth-table reducibility to SAT and the difference hierarchy over NP", Proceedings of Third Annual Structure in Complexity Theory Conference, pp. 224–233, CiteSeerX 10.1.1.5.2387 , doi:10.1109/SCT.1988.5282, ISBN 978-0-8186-0866-7 .

[6] Garey, Michael R.; Johnson, D. S. (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W. H. Freeman.

[7] Aho, A. V. (2011), "Complexity theory", in Blum, E. K.; Aho, A. V. (eds.), Computer Science: The Hardware, Software and Heart of It, pp. 241–267, doi: 10.1007/978-1-4614-1168-0_12 , ISBN 978-1-4614-1167-3 . See in particular p. 255.

[8] Greenlaw, Raymond; Hoover, James; Ruzzo, Walter (1995), Limits To Parallel computation; P-Completeness Theory, ISBN 978-0-19-508591-4 . In particular, for the argument that every nontrivial problem in P has a polynomial-time many-one reduction to every other nontrivial problem, see p. 48.

[9] Schaefer, Marcus (2010), "Complexity of some geometric and topological problems" (PDF), Graph Drawing, 17th International Symposium, GS 2009, Chicago, IL, USA, September 2009, Revised Papers, Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 334–344, doi: 10.1007/978-3-642-11805-0_32 , ISBN 978-3-642-11804-3 .

[10] Köbler, Johannes; Schöning, Uwe; Torán, Jacobo (1993), The Graph Isomorphism Problem: Its Structural Complexity, Birkhäuser, ISBN 978-0-8176-3680-7, OCLC 246882287 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]