Related Research Articles

Supervised learning is the machine learning task of learning a function that maps an input to an output based on example input-output pairs. It infers a function from labeled training data consisting of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value. A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. An optimal scenario will allow for the algorithm to correctly determine the class labels for unseen instances. This requires the learning algorithm to generalize from the training data to unseen situations in a "reasonable" way.

In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on biologically inspired operators such as mutation, crossover and selection. John Holland introduced genetic algorithms in 1960 based on the concept of Darwin’s theory of evolution; his student David E. Goldberg further extended GA in 1989.

In machine learning, support-vector machines are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis. Given a set of training examples, each marked as belonging to one or the other of two categories, an SVM training algorithm builds a model that assigns new examples to one category or the other, making it a non-probabilistic binary linear classifier. An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. New examples are then mapped into that same space and predicted to belong to a category based on the side of the gap on which they fall.
In the field of machine learning, the goal of statistical classification is to use an object's characteristics to identify which class it belongs to. A linear classifier achieves this by making a classification decision based on the value of a linear combination of the characteristics. An object's characteristics are also known as feature values and are typically presented to the machine in a vector called a feature vector. Such classifiers work well for practical problems such as document classification, and more generally for problems with many variables (features), reaching accuracy levels comparable to non-linear classifiers while taking less time to train and use.
Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. To find a local minimum of a function using gradient descent, we take steps proportional to the negative of the gradient of the function at the current point. But if we instead take steps proportional to the positive of the gradient, we approach a local maximum of that function; the procedure is then known as gradient ascent. Gradient descent was originally proposed by Cauchy in 1847.
The Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events, especially in the context of Markov information sources and hidden Markov models (HMM).
In genetic algorithms and evolutionary computation, crossover, also called recombination, is a genetic operator used to combine the genetic information of two parents to generate new offspring. It is one way to stochastically generate new solutions from an existing population, and analogous to the crossover that happens during sexual reproduction in biology. Solutions can also be generated by cloning an existing solution, which is analogous to asexual reproduction. Newly generated solutions are typically mutated before being added to the population.

Statistical learning theory is a framework for machine learning drawing from the fields of statistics and functional analysis. Statistical learning theory deals with the problem of finding a predictive function based on data. Statistical learning theory has led to successful applications in fields such as computer vision, speech recognition, and bioinformatics.
In computer programming, gene expression programming (GEP) is an evolutionary algorithm that creates computer programs or models. These computer programs are complex tree structures that learn and adapt by changing their sizes, shapes, and composition, much like a living organism. And like living organisms, the computer programs of GEP are also encoded in simple linear chromosomes of fixed length. Thus, GEP is a genotype–phenotype system, benefiting from a simple genome to keep and transmit the genetic information and a complex phenotype to explore the environment and adapt to it.

In machine learning and statistics, feature selection, also known as variable selection, attribute selection or variable subset selection, is the process of selecting a subset of relevant features for use in model construction. Feature selection techniques are used for several reasons:
Stochastic gradient descent is an iterative method for optimizing an objective function with suitable smoothness properties. It can be regarded as a stochastic approximation of gradient descent optimization, since it replaces the actual gradient by an estimate thereof. Especially in big data applications this reduces the computational burden, achieving faster iterations in trade for a slightly lower convergence rate.

Estimation of distribution algorithms (EDAs), sometimes called probabilistic model-building genetic algorithms (PMBGAs), are stochastic optimization methods that guide the search for the optimum by building and sampling explicit probabilistic models of promising candidate solutions. Optimization is viewed as a series of incremental updates of a probabilistic model, starting with the model encoding an uninformative prior over admissible solutions and ending with the model that generates only the global optima.
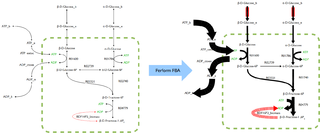
Flux balance analysis (FBA) is a mathematical method for simulating metabolism in genome-scale reconstructions of metabolic networks. In comparison to traditional methods of modeling, FBA is less intensive in terms of the input data required for constructing the model. Simulations performed using FBA are computationally inexpensive and can calculate steady-state metabolic fluxes for large models in a few seconds on modern personal computers.
The combination of quality control and genetic algorithms led to novel solutions of complex quality control design and optimization problems. Quality control is a process by which entities review the quality of all factors involved in production. Quality is the degree to which a set of inherent characteristics fulfils a need or expectation that is stated, general implied or obligatory. Genetic algorithms are search algorithms, based on the mechanics of natural selection and natural genetics.
Isoline retrieval is a remote sensing inverse method that retrieves one or more isolines of a trace atmospheric constituent or variable. When used to validate another contour, it is the most accurate method possible for the task. When used to retrieve a whole field, it is a general, nonlinear inverse method and a robust estimator.
Large margin nearest neighbor (LMNN) classification is a statistical machine learning algorithm for metric learning. It learns a pseudometric designed for k-nearest neighbor classification. The algorithm is based on semidefinite programming, a sub-class of convex optimization.

A restricted Boltzmann machine (RBM) is a generative stochastic artificial neural network that can learn a probability distribution over its set of inputs.
In mathematics, low-rank approximation is a minimization problem, in which the cost function measures the fit between a given matrix and an approximating matrix, subject to a constraint that the approximating matrix has reduced rank. The problem is used for mathematical modeling and data compression. The rank constraint is related to a constraint on the complexity of a model that fits the data. In applications, often there are other constraints on the approximating matrix apart from the rank constraint, e.g., non-negativity and Hankel structure.
Biogeography-based optimization (BBO) is an evolutionary algorithm (EA) that optimizes a function by stochastically and iteratively improving candidate solutions with regard to a given measure of quality, or fitness function. BBO belongs to the class of metaheuristics since it includes many variations, and since it does not make any assumptions about the problem and can therefore be applied to a wide class of problems.
Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. The power of quantum computing may allow solving problems which are not practically feasible on classical computers, or suggest a considerable speed up with respect to the best known classical algorithm. Among other quantum algorithms, there are quantum optimization algorithms which might suggest improvement in solving optimization problems.
References
- ↑ Karray, Fakhreddine O.; de Silva, Clarence (2004), Soft computing and intelligent systems design, Addison Wesley, ISBN 0-321-11617-8
- ↑ Baluja, Shumeet (1994), "Population-Based Incremental Learning: A Method for Integrating Genetic Search Based Function Optimization and Competitive Learning", Technical Report, Pittsburgh, PA: Carnegie Mellon University (CMU–CS–94–163), CiteSeerX 10.1.1.61.8554
- ↑ Baluja, Shumeet; Caruana, Rich (1995), Removing the Genetics from the Standard Genetic Algorithm, Morgan Kaufmann Publishers, pp. 38–46, CiteSeerX 10.1.1.44.5424
- ↑ Baluja, Shumeet (1995), An Empirical Comparison of Seven Iterative and Evolutionary Function Optimization Heuristics, CiteSeerX 10.1.1.43.1108