
A minute of arc, arcminute (arcmin), arc minute, or minute arc, denoted by the symbol ′, is a unit of angular measurement equal to 1/60 of one degree. Since one degree is 1/360 of a turn, or complete rotation, one arcminute is 1/21600 of a turn. The nautical mile (nmi) was originally defined as the arc length of a minute of latitude on a spherical Earth, so the actual Earth circumference is very near 21600 nmi. A minute of arc is π/10800 of a radian.
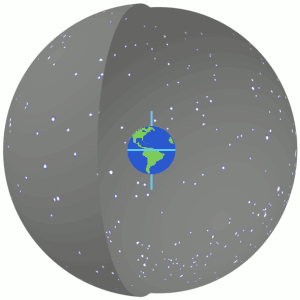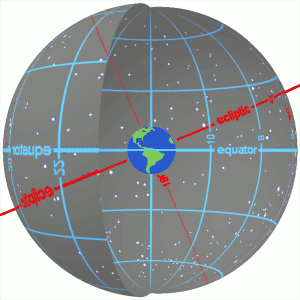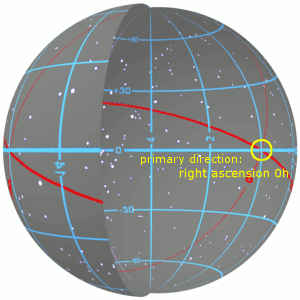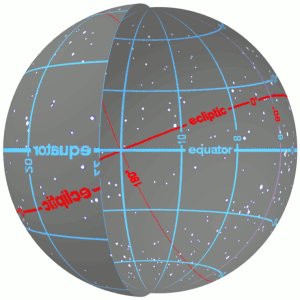
In astronomy, declination is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. The declination angle is measured north (positive) or south (negative) of the celestial equator, along the hour circle passing through the point in question.

Geodesy or geodetics is the science of measuring and representing the geometry, gravity, and spatial orientation of the Earth in temporally varying 3D. It is called planetary geodesy when studying other astronomical bodies, such as planets or circumplanetary systems. Geodesy is an earth science as well as a discipline of applied mathematics, and many consider the study of Earth's shape and gravity to be central to the science.

Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight and is measured by the angle or half-angle of inclination between those two lines. Due to foreshortening, nearby objects show a larger parallax than farther objects, so parallax can be used to determine distances.

Right ascension is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the point in question above the Earth. When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system.
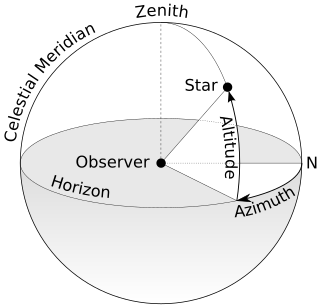
An azimuth is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.

In astronomy, coordinate systems are used for specifying positions of celestial objects relative to a given reference frame, based on physical reference points available to a situated observer. Coordinate systems in astronomy can specify an object's relative position in three-dimensional space or plot merely by its direction on a celestial sphere, if the object's distance is unknown or trivial.

The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere, a primary direction towards the March equinox, and a right-handed convention.

In astronomy, the ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. Because most planets and many small Solar System bodies have orbits with only slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the March equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates.

The galactic coordinate system is a celestial coordinate system in spherical coordinates, with the Sun as its center, the primary direction aligned with the approximate center of the Milky Way Galaxy, and the fundamental plane parallel to an approximation of the galactic plane but offset to its north. It uses the right-handed convention, meaning that coordinates are positive toward the north and toward the east in the fundamental plane.

The zenith is an imaginary point directly "above" a particular location, on the celestial sphere. "Above" means in the vertical direction opposite to the gravity direction at that location (nadir). The zenith is the "highest" point on the celestial sphere.

North is one of the four compass points or cardinal directions. It is the opposite of south and is perpendicular to east and west. North is a noun, adjective, or adverb indicating direction or geography.
Diurnal motion is an astronomical term referring to the apparent motion of celestial objects around Earth, or more precisely around the two celestial poles, over the course of one day. It is caused by Earth's rotation around its axis, so almost every star appears to follow a circular arc path, called the diurnal circle, often depicted in star trail photography.

In navigation, bearing or azimuth is the horizontal angle between the direction of an object and north or another object. The angle value can be specified in various angular units, such as degrees, mils, or grad. More specifically:

The longitude of the ascending node is one of the orbital elements used to specify the orbit of an object in space. It is the angle from a specified reference direction, called the origin of longitude, to the direction of the ascending node (☊), as measured in a specified reference plane. The ascending node is the point where the orbit of the object passes through the plane of reference, as seen in the adjacent image.

The Moon orbits Earth in the prograde direction and completes one revolution relative to the Vernal Equinox and the stars in about 27.32 days and one revolution relative to the Sun in about 29.53 days. Earth and the Moon orbit about their barycentre, which lies about 4,670 km (2,900 mi) from Earth's centre, forming a satellite system called the Earth–Moon system. On average, the distance to the Moon is about 385,000 km (239,000 mi) from Earth's centre, which corresponds to about 60 Earth radii or 1.282 light-seconds.
The poles of astronomical bodies are determined based on their axis of rotation in relation to the celestial poles of the celestial sphere. Astronomical bodies include stars, planets, dwarf planets and small Solar System bodies such as comets and minor planets, as well as natural satellites and minor-planet moons.
In spherical astronomy, the parallactic angle is the angle between the great circle through a celestial object and the zenith, and the hour circle of the object. It is usually denoted q. In the triangle zenith—object—celestial pole, the parallactic angle will be the position angle of the zenith at the celestial object. Despite its name, this angle is unrelated with parallax. The parallactic angle is zero or 180° when the object crosses the meridian.

Two-dimensional rotation can occur in two possible directions or senses of rotation. Clockwise motion proceeds in the same direction as a clock's hands relative to the observer: from the top to the right, then down and then to the left, and back up to the top. The opposite sense of rotation or revolution is anticlockwise (ACW) or counterclockwise (CCW). Three-dimensional rotation can have similarly defined senses when considering the corresponding angular velocity vector.
This glossary of astronomy is a list of definitions of terms and concepts relevant to astronomy and cosmology, their sub-disciplines, and related fields. Astronomy is concerned with the study of celestial objects and phenomena that originate outside the atmosphere of Earth. The field of astronomy features an extensive vocabulary and a significant amount of jargon.















