Related Research Articles
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices are of the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges are of the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

In graph theory, an edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, an exact coloring is a (proper) vertex coloring in which every pair of colors appears on exactly one pair of adjacent vertices. That is, it is a partition of the vertices of the graph into disjoint independent sets such that, for each pair of distinct independent sets in the partition, there is exactly one edge with endpoints in each set.
In the mathematical area of graph theory, a chordal graph is one in which all cycles of four or more vertices have a chord, which is an edge that is not part of the cycle but connects two vertices of the cycle. Equivalently, every induced cycle in the graph should have exactly three vertices. The chordal graphs may also be characterized as the graphs that have perfect elimination orderings, as the graphs in which each minimal separator is a clique, and as the intersection graphs of subtrees of a tree. They are sometimes also called rigid circuit graphs or triangulated graphs.

In graph theory, a circle graph is the intersection graph of a chord diagram. That is, it is an undirected graph whose vertices can be associated with a finite system of chords of a circle such that two vertices are adjacent if and only if the corresponding chords cross each other.
In graph theory, the metric dimension of a graph G is the minimum cardinality of a subset S of vertices such that all other vertices are uniquely determined by their distances to the vertices in S. Finding the metric dimension of a graph is an NP-hard problem; the decision version, determining whether the metric dimension is less than a given value, is NP-complete.
In graph theory, the treewidth of an undirected graph is an integer number which specifies, informally, how far the graph is from being a tree. The smallest treewidth is 1; the graphs with treewidth 1 are exactly the trees and the forests. The graphs with treewidth at most 2 are the series–parallel graphs. The maximal graphs with treewidth exactly k are called k-trees, and the graphs with treewidth at most k are called partial k-trees. Many other well-studied graph families also have bounded treewidth.

In graph theory, a book embedding is a generalization of planar embedding of a graph to embeddings into a book, a collection of half-planes all having the same line as their boundary. Usually, the vertices of the graph are required to lie on this boundary line, called the spine, and the edges are required to stay within a single half-plane. The book thickness of a graph is the smallest possible number of half-planes for any book embedding of the graph. Book thickness is also called pagenumber, stacknumber or fixed outerthickness. Book embeddings have also been used to define several other graph invariants including the pagewidth and book crossing number.

In graph theory, the Grundy number or Grundy chromatic number of an undirected graph is the maximum number of colors that can be used by a greedy coloring strategy that considers the vertices of the graph in sequence and assigns each vertex its first available color, using a vertex ordering chosen to use as many colors as possible. Grundy numbers are named after P. M. Grundy, who studied an analogous concept for directed graphs in 1939. The undirected version was introduced by Christen & Selkow (1979).

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and each edge connects two squares on the same row (rank) or on the same column (file) as each other, the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape, and can be defined mathematically as the Cartesian product of two complete graphs, as the two-dimensional Hamming graphs, or as the line graphs of complete bipartite graphs.

In graph theory, the clique-width of a graph G is a parameter that describes the structural complexity of the graph; it is closely related to treewidth, but unlike treewidth it can be bounded even for dense graphs. It is defined as the minimum number of labels needed to construct G by means of the following 4 operations :
- Creation of a new vertex v with label i
- Disjoint union of two labeled graphs G and H
- Joining by an edge every vertex labeled i to every vertex labeled j, where i ≠ j
- Renaming label i to label j
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.
In graph theory, a perfectly orderable graph is a graph whose vertices can be ordered in such a way that a greedy coloring algorithm with that ordering optimally colors every induced subgraph of the given graph. Perfectly orderable graphs form a special case of the perfect graphs, and they include the chordal graphs, comparability graphs, and distance-hereditary graphs. However, testing whether a graph is perfectly orderable is NP-complete.
In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that
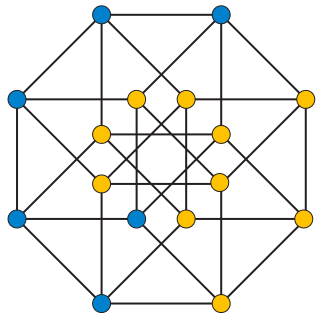
In graph theory, a distinguishing coloring or distinguishing labeling of a graph is an assignment of colors or labels to the vertices of the graph that destroys all of the nontrivial symmetries of the graph. The coloring does not need to be a proper coloring: adjacent vertices are allowed to be given the same color. For the colored graph, there should not exist any one-to-one mapping of the vertices to themselves that preserves both adjacency and coloring. The minimum number of colors in a distinguishing coloring is called the distinguishing number of the graph.
In graph theory, a branch of mathematics, a chordal completion of a given undirected graph G is a chordal graph, on the same vertex set, that has G as a subgraph. A minimal chordal completion is a chordal completion such that any graph formed by removing an edge would no longer be a chordal completion. A minimum chordal completion is a chordal completion with as few edges as possible.
In graph theory, an induced matching or strong matching is a subset of the edges of an undirected graph that do not share any vertices and includes every edge connecting any two vertices in the subset.

In the mathematics of Sudoku, the Sudoku graph is an undirected graph whose vertices represent the cells of a (blank) Sudoku puzzle and whose edges represent pairs of cells that belong to the same row, column, or block of the puzzle. The problem of solving a Sudoku puzzle can be represented as precoloring extension on this graph. It is an integral Cayley graph.
References
- ↑ Colbourn, Charles J. (1984), "The complexity of completing partial Latin squares", Discrete Applied Mathematics, 8 (1): 25–30, doi: 10.1016/0166-218X(84)90075-1 , MR 0739595 .
- 1 2 Jansen, Klaus; Scheffler, Petra (1997), "Generalized coloring for tree-like graphs", Discrete Applied Mathematics, 75 (2): 135–155, doi: 10.1016/S0166-218X(96)00085-6 , MR 1451958
- ↑ Fellows, Michael R.; Fomin, Fedor V.; Lokshtanov, Daniel; Rosamond, Frances; Saurabh, Saket; Szeider, Stefan; Thomassen, Carsten (2011), "On the complexity of some colorful problems parameterized by treewidth", Information and Computation, 209 (2): 143–153, doi:10.1016/j.ic.2010.11.026, MR 2790022
- ↑ Herzberg, Agnes M.; Murty, M. Ram (2007), "Sudoku squares and chromatic polynomials", Notices of the American Mathematical Society , 54 (6): 708–717, MR 2327972
- ↑ Rosenhouse, Jason; Taalman, Laura (2011), Taking Sudoku Seriously: The math behind the world's most popular pencil puzzle, Oxford University Press, p. 130