In mathematics, a binary relation over sets X and Y is a subset of the Cartesian product ; that is, it is a set of ordered pairs (x, y) consisting of elements x in X and y in Y. It encodes the common concept of relation: an element x is related to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. A binary relation is the most studied special case n = 2 of an n-ary relation over sets X1, ..., Xn, which is a subset of the Cartesian product

In economics, an indifference curve connects points on a graph representing different quantities of two goods, points between which a consumer is indifferent. That is, any combinations of two products indicated by the curve will provide the consumer with equal levels of utility, and the consumer has no preference for one combination or bundle of goods over a different combination on the same curve. One can also refer to each point on the indifference curve as rendering the same level of utility (satisfaction) for the consumer. In other words, an indifference curve is the locus of various points showing different combinations of two goods providing equal utility to the consumer. Utility is then a device to represent preferences rather than something from which preferences come. The main use of indifference curves is in the representation of potentially observable demand patterns for individual consumers over commodity bundles.

In machine learning, boosting is an ensemble meta-algorithm for primarily reducing bias, and also variance in supervised learning, and a family of machine learning algorithms that convert weak learners to strong ones. Boosting is based on the question posed by Kearns and Valiant : "Can a set of weak learners create a single strong learner?" A weak learner is defined to be a classifier that is only slightly correlated with the true classification. In contrast, a strong learner is a classifier that is arbitrarily well-correlated with the true classification.
Euclidean is an adjective derived from the name of Euclid, an ancient Greek mathematician. It is the name of:
In mathematics, a relation R on a set X is transitive if, for all elements a, b, c in X, whenever R relates a to b and b to c, then R also relates a to c. Each partial order as well as each equivalence relation needs to be transitive.

In mathematics, particularly graph theory, and computer science, a directed acyclic graph is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that following those directions will never form a closed loop. A directed graph is a DAG if and only if it can be topologically ordered, by arranging the vertices as a linear ordering that is consistent with all edge directions. DAGs have numerous scientific and computational applications, ranging from biology to sociology to computation (scheduling).

Unsupervised learning (UL) is a type of algorithm that learns patterns from untagged data. The hope is that, through mimicry, the machine is forced to build a compact internal representation of its world and then generate imaginative content. In contrast to supervised learning (SL) where data is tagged by a human, e.g. as "car" or "fish" etc, UL exhibits self-organization that captures patterns as neuronal predilections or probability densities. The other levels in the supervision spectrum are reinforcement learning where the machine is given only a numerical performance score as its guidance, and semi-supervised learning where a smaller portion of the data is tagged. Two broad methods in UL are Neural Networks and Probabilistic Methods.
In mathematics, the transitive closure of a binary relation R on a set X is the smallest relation on X that contains R and is transitive. For finite sets, "smallest" can be taken in its usual sense, of having the fewest related pairs; for infinite sets it is the unique minimal transitive superset of R.
In mathematics, intransitivity is a property of binary relations that are not transitive relations. This may include any relation that is not transitive, or the stronger property of antitransitivity, which describes a relation that is never transitive.

In mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set, some of whose members may be tied with each other. Weak orders are a generalization of totally ordered sets and are in turn generalized by partially ordered sets and preorders.

Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (MCDA) is a sub-discipline of operations research that explicitly evaluates multiple conflicting criteria in decision making. Conflicting criteria are typical in evaluating options: cost or price is usually one of the main criteria, and some measure of quality is typically another criterion, easily in conflict with the cost. In purchasing a car, cost, comfort, safety, and fuel economy may be some of the main criteria we consider – it is unusual that the cheapest car is the most comfortable and the safest one. In portfolio management, managers are interested in getting high returns while simultaneously reducing risks; however, the stocks that have the potential of bringing high returns typically carry high risk of losing money. In a service industry, customer satisfaction and the cost of providing service are fundamental conflicting criteria.
Order in mathematics may refer to:
In mathematics, a binary relation over sets X and Y is a subset of the Cartesian product X × Y; that is, it is a set of ordered pairs (x, y) consisting of elements x in X and y in Y. It encodes the common concept of relation: an element x is related to an element y, if and only if the pair (x, y) belongs to the set of ordered pairs that defines the binary relation. A binary relation is the most studied special case n = 2 of an n-ary relation over sets X1, ..., Xn, which is a subset of the Cartesian product X1 × ... × Xn.

Learning to rank or machine-learned ranking (MLR) is the application of machine learning, typically supervised, semi-supervised or reinforcement learning, in the construction of ranking models for information retrieval systems. Training data consists of lists of items with some partial order specified between items in each list. This order is typically induced by giving a numerical or ordinal score or a binary judgment for each item. The ranking model purposes to rank, i.e. producing a permutation of items in new, unseen lists in a similar way to rankings in the training data.
In economics and other social sciences, preference is the order that a person gives to alternatives based on their relative utility, a process which results in an optimal "choice". Preferences are evaluations, they concern matters of value, typically in relation to practical reasoning. Instead of the prices of goods, personal income, or availability of goods, the character of the preferences is determined purely by a person's tastes. However, persons are still expected to act in their best interest. Rationality suggests that people act in ways which serves their best interest when they are faced with a decision. Meaning when given a set of options, you must necessarily have a set of preferences.
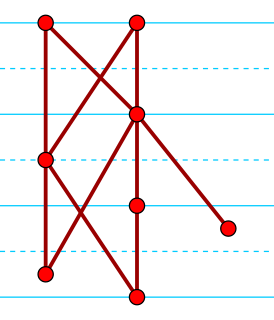
In order theory, a branch of mathematics, a semiorder is a type of ordering for items with numerical scores, where items with widely differing scores are compared by their scores and where scores within a given margin of error are deemed incomparable. Semiorders were introduced and applied in mathematical psychology by Duncan Luce (1956) as a model of human preference. They generalize strict weak orderings, in which items with equal scores may be tied but there is no margin of error. They are a special case of partial orders and of interval orders, and can be characterized among the partial orders by additional axioms, or by two forbidden four-item suborders.
Preference learning is a subfield in machine learning, which is a classification method based on observed preference information. In the view of supervised learning, preference learning trains on a set of items which have preferences toward labels or other items and predicts the preferences for all items.
A participatory budgeting (PB) algorithm is an algorithm for implementing participatory budgeting.
Stochastic transitivity models are stochastic versions of the transitivity property of binary relations studied in mathematics. Several models of stochastic transitivity exist and have been used to describe the probabilities involved in experiments of paired comparisons, specifically in scenarios where transitivity is expected, however, empirical observations of the binary relation is probabilistic. For example, players' skills in a sport might be expected to be transitive, i.e. "if player A is better than B and B is better than C, then player A must be better than C"; however, in any given match, a weaker player might still end up winning with a positive probability. Tighly matched players might have a higher chance of observing this inversion while players with large differences in their skills might only see these inversions happen seldomly. Stochastic transitivity models formalize such relations between the probabilities and the underlying transitive relation.
In economics and computer science, the house allocation problem is the problem of assigning objects to people with different preferenes, such that each person receives exactly one object. The name "house allocation" comes from the main motivating application, which is assigning dormitory houses to students. Other commonly used terms are assignment problem and one-sided matching. In house allocation problems, it is assumed that monetary transfers are not allowed; the variant in which monetary transfers are allowed is known as rental harmony.





