A context-sensitive grammar (CSG) is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols. Context-sensitive grammars are more general than context-free grammars, in the sense that there are languages that can be described by CSG but not by context-free grammars. Context-sensitive grammars are less general than unrestricted grammars. Thus, CSG are positioned between context-free and unrestricted grammars in the Chomsky hierarchy.
In formal language theory, a context-free grammar (CFG) is a certain type of formal grammar: a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the rule
In formal language theory, a context-free language (CFL) is a language generated by a context-free grammar (CFG).

In mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules.
In theoretical computer science and formal language theory, a regular grammar is a formal grammar that is right-regular or left-regular. Every regular grammar describes a regular language.
Categorial grammar is a term used for a family of formalisms in natural language syntax motivated by the principle of compositionality and organized according to the view that syntactic constituents should generally combine as functions or according to a function-argument relationship. Most versions of categorial grammar analyze sentence structure in terms of constituencies and are therefore phrase structure grammars.
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton that maps between two sets of symbols. An FST is more general than a finite-state automaton (FSA). An FSA defines a formal language by defining a set of accepted strings, while an FST defines relations between sets of strings.
In theoretical computer science and mathematical logic a string rewriting system (SRS), historically called a semi-Thue system, is a rewriting system over strings from a alphabet. Given a binary relation between fixed strings over the alphabet, called rewrite rules, denoted by , an SRS extends the rewriting relation to all strings in which the left- and right-hand side of the rules appear as substrings, that is , where , , , and are strings.
Conjunctive grammars are a class of formal grammars studied in formal language theory. They extend the basic type of grammars, the context-free grammars, with a conjunction operation. Besides explicit conjunction, conjunctive grammars allow implicit disjunction represented by multiple rules for a single nonterminal symbol, which is the only logical connective expressible in context-free grammars. Conjunction can be used, in particular, to specify intersection of languages. A further extension of conjunctive grammars known as Boolean grammars additionally allows explicit negation.
In formal language theory, a string is defined as a finite sequence of members of an underlying base set; this set is called the alphabet of a string or collection of strings. The members of the set are called symbols, and are typically thought of as representing letters, characters, or digits. For example, a common alphabet is {0,1}, the binary alphabet, and a binary string is a string drawn from the alphabet {0,1}. An infinite sequence of letters may be constructed from elements of an alphabet as well.
In computer science, terminal and nonterminal symbols are the lexical elements used in specifying the production rules constituting a formal grammar. Terminal symbols are the elementary symbols of the language defined by a formal grammar. Nonterminal symbols are replaced by groups of terminal symbols according to the production rules.
In computer science, in the area of formal language theory, frequent use is made of a variety of string functions; however, the notation used is different from that used for computer programming, and some commonly used functions in the theoretical realm are rarely used when programming. This article defines some of these basic terms.
Indexed grammars are a generalization of context-free grammars in that nonterminals are equipped with lists of flags, or index symbols. The language produced by an indexed grammar is called an indexed language.
A production or production rule in computer science is a rewrite rule specifying a symbol substitution that can be recursively performed to generate new symbol sequences. A finite set of productions is the main component in the specification of a formal grammar. The other components are a finite set of nonterminal symbols, a finite set of terminal symbols that is disjoint from and a distinguished symbol that is the start symbol.
In formal language theory, a grammar is a set of production rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.
Controlled grammars are a class of grammars that extend, usually, the context-free grammars with additional controls on the derivations of a sentence in the language. A number of different kinds of controlled grammars exist, the four main divisions being Indexed grammars, grammars with prescribed derivation sequences, grammars with contextual conditions on rule application, and grammars with parallelism in rule application. Because indexed grammars are so well established in the field, this article will address only the latter three kinds of controlled grammars.
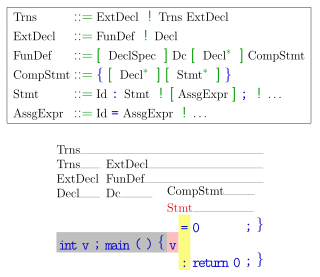
In formal language theory, an LL grammar is a context-free grammar that can be parsed by an LL parser, which parses the input from Left to right, and constructs a Leftmost derivation of the sentence. A language that has an LL grammar is known as an LL language. These form subsets of deterministic context-free grammars (DCFGs) and deterministic context-free languages (DCFLs), respectively. One says that a given grammar or language "is an LL grammar/language" or simply "is LL" to indicate that it is in this class.
In theoretical computer science, a pattern language is a formal language that can be defined as the set of all particular instances of a string of constants and variables. Pattern Languages were introduced by Dana Angluin in the context of machine learning.







