 Front cover | |
| Author | Christel Baier and Joost-Pieter Katoen |
|---|---|
| Subject | Model checking |
| Publisher | MIT Press |
Publication date | 25 April 2008 |
| Pages | 975 |
| ISBN | 9780262026499 |
Principles of Model Checking is a textbook on model checking, an area of computer science that automates the problem of determining if a machine meets specification requirements. It was written by Christel Baier and Joost-Pieter Katoen, and published in 2008 by MIT Press.
The introduction and first chapter outline the field of model checking: a model of a machine or process can be analysed to see if desirable properties hold. For instance, a vending machine might satisfy the property "the balance can never fall below €0,00". A video game might enforce the rule "if the player has 0 lives then the game ends in a loss". Both the vending machine and video game can be modelled as transition systems. Model checking is the process of describing such requirements in mathematical language, and automating proofs that the model satisfies the requirements, or discovery of counterexamples if the model is faulty.
The second chapter focuses on creating an appropriate model for concurrent systems, where multiple parts of an algorithm (set of instructions) can be carried out simultaneously by different machines or parts of a machine.
Chapters 3 explores types of rules that a transition system may satisfy: linear time properties. A safety property, such as "no deadlock states are possible", is of the form "an undesirable outcome can never occur". A liveness property, such as "a shared resource will always eventually be made available to a component that requests it", is of the form "a desirable outcome will eventually happen". Fairness properties such as "a traffic light never stops changing colour" can be used as preconditions i.e. assumptions from which other properties can be deduced.
The fourth chapter is about regular and ω-regular language properties, and theoretical machines such as Büchi automata that model the languages. It gives model-checking algorithms to verify properties or find counterexamples.
The fifth and sixth chapters explore linear temporal logic (LTL) and computation tree logic (CTL), two classes of formula that express properties. LTL encodes requirements about paths through a system, such as "every Monopoly player passes 'Go' infinitely often"; CTL encodes requirements about states in a system, such as "from any position, all players can eventually land on 'Go'". CTL* formulae, which combine the two grammars, are also defined. Algorithms for model-checking formulae in these logics are given.
The seventh chapter explores formal ways to compare transition systems, such as bisimulation; the eighth is about partial order reductions that aim to reduce the computation required to verify properties of a model. The ninth and tenth chapters are about extensions to the logics and automata previously considered, including through addition of a clock speed (timed automata) or probabilities (probabilistic automata, based on Markov chains).
François Laroussinie, writing in The Computer Journal , recommended the book to researchers, lecturers, students and engineers, calling the book "impressive". Laroussinie found the textbook comprehensive and accessibly written, with a good number of examples, exercises and motivating ideas for key concepts. With a "unified framework", the first seven chapters cover classical theory and the last three chapters cover extensions of model checking. [1]
In ACM Computing Reviews , Gabriel Ciobanu believed the textbook could be used in advanced undergraduate or graduate courses, and would be useful to researchers. Ciobanu praised the "clear and intuitive" presentation and said it "should be appreciated for its pedagogical approach to covering basic concepts, deep theoretical results, and advanced topics in model checking research". [2]
In 2014, the book was one of the five most-cited academic texts monitored by the Book Citation Index (BKCI). [3]
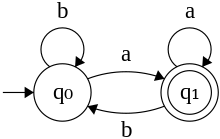
A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.
In computer science, formal methods are mathematically rigorous techniques for the specification, development, analysis, and verification of software and hardware systems. The use of formal methods for software and hardware design is motivated by the expectation that, as in other engineering disciplines, performing appropriate mathematical analysis can contribute to the reliability and robustness of a design.
Computer science is the study of the theoretical foundations of information and computation and their implementation and application in computer systems. One well known subject classification system for computer science is the ACM Computing Classification System devised by the Association for Computing Machinery.
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of a system with respect to a certain formal specification or property, using formal methods of mathematics. Formal verification is a key incentive for formal specification of systems, and is at the core of formal methods. It represents an important dimension of analysis and verification in electronic design automation and is one approach to software verification. The use of formal verification enables the highest Evaluation Assurance Level (EAL7) in the framework of common criteria for computer security certification.
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification. This is typically associated with hardware or software systems, where the specification contains liveness requirements as well as safety requirements.
In logic, linear temporal logic or linear-time temporal logic (LTL) is a modal temporal logic with modalities referring to time. In LTL, one can encode formulae about the future of paths, e.g., a condition will eventually be true, a condition will be true until another fact becomes true, etc. It is a fragment of the more complex CTL*, which additionally allows branching time and quantifiers. LTL is sometimes called propositional temporal logic, abbreviated PTL. In terms of expressive power, linear temporal logic (LTL) is a fragment of first-order logic.
Property Specification Language (PSL) is a temporal logic extending linear temporal logic with a range of operators for both ease of expression and enhancement of expressive power. PSL makes an extensive use of regular expressions and syntactic sugaring. It is widely used in the hardware design and verification industry, where formal verification tools and/or logic simulation tools are used to prove or refute that a given PSL formula holds on a given design.
Computation tree logic (CTL) is a branching-time logic, meaning that its model of time is a tree-like structure in which the future is not determined; there are different paths in the future, any one of which might be an actual path that is realized. It is used in formal verification of software or hardware artifacts, typically by software applications known as model checkers, which determine if a given artifact possesses safety or liveness properties. For example, CTL can specify that when some initial condition is satisfied, then all possible executions of a program avoid some undesirable condition. In this example, the safety property could be verified by a model checker that explores all possible transitions out of program states satisfying the initial condition and ensures that all such executions satisfy the property. Computation tree logic belongs to a class of temporal logics that includes linear temporal logic (LTL). Although there are properties expressible only in CTL and properties expressible only in LTL, all properties expressible in either logic can also be expressed in CTL*.
SPIN is a general tool for verifying the correctness of concurrent software models in a rigorous and mostly automated fashion. It was written by Gerard J. Holzmann and others in the original Unix group of the Computing Sciences Research Center at Bell Labs, beginning in 1980. The software has been available freely since 1991, and continues to evolve to keep pace with new developments in the field.
In theoretical computer science, the modal μ-calculus is an extension of propositional modal logic by adding the least fixed point operator μ and the greatest fixed point operator ν, thus a fixed-point logic.
CTL* is a superset of computational tree logic (CTL) and linear temporal logic (LTL). It freely combines path quantifiers and temporal operators. Like CTL, CTL* is a branching-time logic. The formal semantics of CTL* formulae are defined with respect to a given Kripke structure.
CADP is a toolbox for the design of communication protocols and distributed systems. CADP is developed by the CONVECS team at INRIA Rhone-Alpes and connected to various complementary tools. CADP is maintained, regularly improved, and used in many industrial projects.
In automata theory, a semi-deterministic Büchi automaton is a special type of Büchi automaton. In such an automaton, the set of states can be partitioned into two subsets: one subset forms a deterministic automaton and also contains all the accepting states.
In automata theory, a generalized Büchi automaton is a variant of a Büchi automaton. The difference with the Büchi automaton is the accepting condition, which is determined by a set of sets of states. A run is accepted by the automaton if it visits at least one state of every set of the accepting condition infinitely often. Generalized Büchi automata are equivalent in expressive power to Büchi automata; a transformation is given here.
TAPAAL is a tool for modelling, simulation and verification of Timed-Arc Petri nets developed at Department of Computer Science at Aalborg University in Denmark and it is available for Linux, Windows and Mac OS X platforms.
In model checking, a branch of computer science, linear time properties are used to describe requirements of a model of a computer system. Example properties include "the vending machine does not dispense a drink until money has been entered" or "the computer program eventually terminates". Fairness properties can be used to rule out unrealistic paths of a model. For instance, in a model of two traffic lights, the liveness property "both traffic lights are green infinitely often" may only be true under the unconditional fairness constraint "each traffic light changes colour infinitely often".
Christel Baier is a German theoretical computer scientist known for her work in model checking, temporal logic, and automata theory. She is a professor at TU Dresden, where she holds the chair for Algebraic and Logic Foundations of Computer Science in the Faculty of Computer Science. Baier is the editor-in-chief of Acta Informatica.
In computer science, hyperproperties are a formalism for describing properties of computational systems. Hyperproperties generalize safety and liveness properties, and can express properties such as non-interference and observational determinism.
Counterexample-guided abstraction refinement (CEGAR) is a technique for symbolic model checking. It is also applied in modal logic tableau calculi algorithms to optimise their efficiency.
{{citation}}: CS1 maint: untitled periodical (link)