ProbCons

Last updated October 26, 2020

ProbCons is an open source probabilistic consistency-based multiple alignment of amino acid sequences. It is one of the most efficient protein multiple sequence alignment programs, since it has repeatedly demonstrated a statistically significant advantage in accuracy over similar tools, including Clustal and MAFFT.^[1]^[2]

Algorithm

The following describes the basic outline of the ProbCons algorithm.^[3]

Step 1: Reliability of an alignment edge

For every pair of sequences compute the probability that letters $x_{i}$ and $y_{i}$ are paired in $a^{*}$ an alignment that is generated by the model.

${\begin{aligned}P(x_{i}\sim y_{i}|x,y)&{\stackrel {def}{=}}Pr[x_{i}\sim y_{i}{\text{ in some a }}|x,y]\\&=\sum _{{\text{alignment a with }}x_{i}-y_{i}}Pr[a|x,y]\\&=\sum _{\text{alignment a}}\mathbf {1} \{x_{i}-y_{i}\in a\}Pr[a|x,y]\end{aligned}}$

(Where $\mathbf {1} \{x_{i}\sim y_{i}\in a\}$ is equal to 1 if $x_{i}$ and $y_{i}$ are in the alignment and 0 otherwise.)

Step 2: Maximum expected accuracy

The accuracy of an alignment $a^{*}$ with respect to another alignment $a$ is defined as the number of common aligned pairs divided by the length of the shorter sequence.

Calculate expected accuracy of each sequence:

${\begin{aligned}E_{Pr[a|x,y]}(acc(a^{*},a))&=\sum _{a}Pr[a|x,y]acc(a^{*},a)\\&={\frac {1}{min(|x|,|y|)}}\cdot \sum _{a}\mathbf {1} \{x_{i}\sim y_{i}\in a\}Pr[a|x,y]\\&={\frac {1}{min(|x|,|y|)}}\cdot \sum _{x_{i}-y_{i}}P(x_{i}\sim y_{j}|x,y)\end{aligned}}$

This yields a maximum expected accuracy (MEA) alignment:

$E(x,y)=\arg \max _{a^{*}}\;E_{Pr[a|x,y]}(acc(a^{*},a))$

Step 3: Probabilistic Consistency Transformation

All pairs of sequences x,y from the set of all sequences ${\mathcal {S}}$ are now re-estimated using all intermediate sequences z:

$P'(x_{i}-y_{i}|x,y)={\frac {1}{|{\mathcal {S}}|}}\sum _{z}\sum _{1\leq k\leq |z|}P(x_{i}\sim z_{i}|x,z)\cdot P(z_{i}\sim y_{i}|z,y)$

This step can be iterated.

Step 4: Computation of guide tree

Construct a guide tree by hierarchical clustering using MEA score as sequence similarity score. Cluster similarity is defined using weighted average over pairwise sequence similarity.

Step 5: Compute MSA

Finally compute the MSA using progressive alignment or iterative alignment.

Related Research Articles

In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's energy spectrum or its set of energy eigenvalues, is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory.

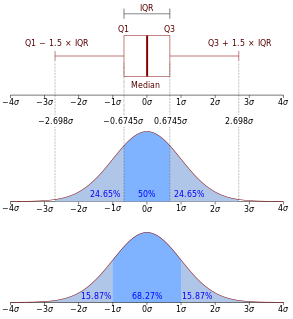
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample in the sample space can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample. In other words, while the absolute likelihood for a continuous random variable to take on any particular value is 0, the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would equal one sample compared to the other sample.

In probability theory and statistics, the geometric distribution is either of two discrete probability distributions:

Multivariate normal distribution Generalization of the one-dimensional normal distribution to higher dimensions

In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.

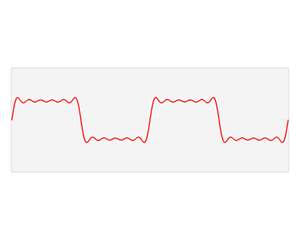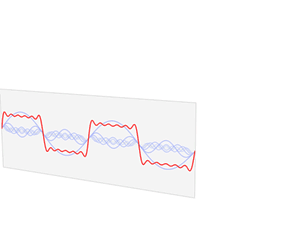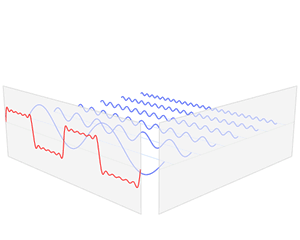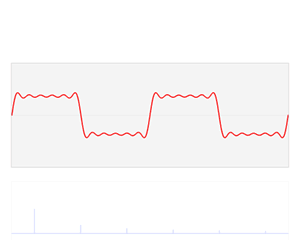
Fourier series Decomposition of periodic functions into sums of simpler sinusoidal forms

In mathematics, a Fourier series is a periodic function composed of harmonically related sinusoids, combined by a weighted summation. With appropriate weights, one cycle of the summation can be made to approximate an arbitrary function in that interval. As such, the summation is a synthesis of another function. The discrete-time Fourier transform is an example of Fourier series. The process of deriving the weights that describe a given function is a form of Fourier analysis. For functions on unbounded intervals, the analysis and synthesis analogies are Fourier transform and inverse transform.

In mathematics, Stirling's approximation is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of $n$ . It is named after James Stirling, though it was first stated by Abraham de Moivre.

In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values,, the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other,, the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation.

Moment of inertia Scalar measure of the rotational inertia with respect to a fixed axis of rotation

The moment of inertia, otherwise known as the mass moment of inertia, angular mass or rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis; similar to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation.

In statistics, the logistic model is used to model the probability of a certain class or event existing such as pass/fail, win/lose, alive/dead or healthy/sick. This can be extended to model several classes of events such as determining whether an image contains a cat, dog, lion, etc. Each object being detected in the image would be assigned a probability between 0 and 1, with a sum of one.

In physics, an operator is a function over a space of physical states onto another space of physical states. The simplest example of the utility of operators is the study of symmetry. Because of this, they are very useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.

This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.

Hotellings <i>T</i>-squared distribution

In statistics, particularly in hypothesis testing, the Hotelling's T-squared distribution (T²), proposed by Harold Hotelling, is a multivariate probability distribution that is tightly related to the F-distribution and is most notable for arising as the distribution of a set of sample statistics that are natural generalizations of the statistics underlying the Student's t-distribution.

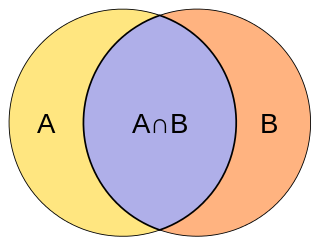
The Jaccard index, also known as Intersection over Union and the Jaccard similarity coefficient, is a statistic used for gauging the similarity and diversity of sample sets. The Jaccard coefficient measures similarity between finite sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets:

The following are important identities involving derivatives and integrals in vector calculus.

In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed dependent variable, given a set of independent variables.

CS-BLAST (Context-Specific BLAST) is a tool that searches a protein sequence that extends BLAST, using context-specific mutation probabilities. More specifically, CS-BLAST derives context-specific amino-acid similarities on each query sequence from short windows on the query sequences [4]. Using CS-BLAST doubles sensitivity and significantly improves alignment quality without a loss of speed in comparison to BLAST. CSI-BLAST is the context-specific analog of PSI-BLAST, which computes the mutation profile with substitution probabilities and mixes it with the query profile [2]. CSI-BLAST is the context specific analog of PSI-BLAST. Both of these programs are available as web-server and are available for free download.

The quantization of the electromagnetic field, means that an electromagnetic field consists of discrete energy parcels, photons. Photons are massless particles of definite energy, definite momentum, and definite spin.

For certain applications in linear algebra, it is useful to know properties of the probability distribution of the largest eigenvalue of a finite sum of random matrices. Suppose $is a finite sequence of random matrices. Analogous to the well-known Chernoff bound for sums of scalars, a bound on the following is sought for a given parameter t :$

Probalign is a sequence alignment tool that calculates a maximum expected accuracy alignment using partition function posterior probabilities. Base pair probabilities are estimated using an estimate similar to Boltzmann distribution. The partition function is calculated using a dynamic programming approach.

In physics, relativistic angular momentum refers to the mathematical formalisms and physical concepts that define angular momentum in special relativity (SR) and general relativity (GR). The relativistic quantity is subtly different from the three-dimensional quantity in classical mechanics.

References

↑ Do CB, Mahabhashyam MS, Brudno M, Batzoglou S (2005). "PROBCONS: Probabilistic Consistency-based Multiple Sequence Alignment". Genome Research. 15 (2): 330–340. doi:10.1101/gr.2821705. PMC 546535 . PMID 15687296.
↑ Roshan, Usman (2014-01-01). "Multiple Sequence Alignment Using Probcons and Probalign". In Russell, David J (ed.). Multiple Sequence Alignment Methods. Methods in Molecular Biology. 1079. Humana Press. pp. 147–153. doi:10.1007/978-1-62703-646-7_9. ISBN 9781627036450. PMID 24170400.
↑ Lecture "Bioinformatics II" at University of Freiburg

External links

Official website

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Do CB, Mahabhashyam MS, Brudno M, Batzoglou S (2005). "PROBCONS: Probabilistic Consistency-based Multiple Sequence Alignment". Genome Research. 15 (2): 330–340. doi:10.1101/gr.2821705. PMC 546535 . PMID 15687296.

[2] Roshan, Usman (2014-01-01). "Multiple Sequence Alignment Using Probcons and Probalign". In Russell, David J (ed.). Multiple Sequence Alignment Methods. Methods in Molecular Biology. 1079. Humana Press. pp. 147–153. doi:10.1007/978-1-62703-646-7_9. ISBN 9781627036450. PMID 24170400.

[3] Lecture "Bioinformatics II" at University of Freiburg