Supervised learning is the machine learning task of learning a function that maps an input to an output based on example input-output pairs. It infers a function from labeled training data consisting of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value. A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. An optimal scenario will allow for the algorithm to correctly determine the class labels for unseen instances. This requires the learning algorithm to generalize from the training data to unseen situations in a "reasonable" way.
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability".
In statistics, Naive Bayes classifiers are a family of simple "probabilistic classifiers" based on applying Bayes' theorem with strong (naïve) independence assumptions between the features. They are among the simplest Bayesian network models. But they could be coupled with Kernel density estimation and achieve higher accuracy levels.
In the field of machine learning, the goal of statistical classification is to use an object's characteristics to identify which class it belongs to. A linear classifier achieves this by making a classification decision based on the value of a linear combination of the characteristics. An object's characteristics are also known as feature values and are typically presented to the machine in a vector called a feature vector. Such classifiers work well for practical problems such as document classification, and more generally for problems with many variables (features), reaching accuracy levels comparable to non-linear classifiers while taking less time to train and use.
Pattern recognition is the automated recognition of patterns and regularities in data. It has applications in statistical data analysis, signal processing, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Pattern recognition has its origins in statistics and engineering; some modern approaches to pattern recognition include the use of machine learning, due to the increased availability of big data and a new abundance of processing power. However, these activities can be viewed as two facets of the same field of application, and together they have undergone substantial development over the past few decades. A modern definition of pattern recognition is:
The field of pattern recognition is concerned with the automatic discovery of regularities in data through the use of computer algorithms and with the use of these regularities to take actions such as classifying the data into different categories.
In Bayesian statistical inference, a prior probability distribution, often simply called the prior, of an uncertain quantity is the probability distribution that would express one's beliefs about this quantity before some evidence is taken into account. For example, the prior could be the probability distribution representing the relative proportions of voters who will vote for a particular politician in a future election. The unknown quantity may be a parameter of the model or a latent variable rather than an observable variable.
In statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which a future observation will fall, with a certain probability, given what has already been observed. Prediction intervals are often used in regression analysis.
Decision tree learning is one of the predictive modelling approaches used in statistics, data mining and machine learning. It uses a decision tree to go from observations about an item to conclusions about the item's target value. Tree models where the target variable can take a discrete set of values are called classification trees; in these tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels. Decision trees where the target variable can take continuous values are called regression trees. Decision trees are among the most popular machine learning algorithms given their intelligibility and simplicity.
In the field of machine learning and specifically the problem of statistical classification, a confusion matrix, also known as an error matrix, is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one. Each row of the matrix represents the instances in a predicted class while each column represents the instances in an actual class. The name stems from the fact that it makes it easy to see if the system is confusing two classes.
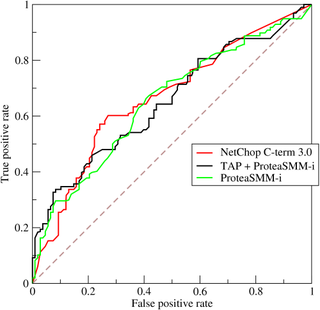
A receiver operating characteristic curve, or ROC curve, is a graphical plot that illustrates the diagnostic ability of a binary classifier system as its discrimination threshold is varied. The method was developed for operators of military radar receivers, which is why it is so named.
In statistics, classification is the problem of identifying to which of a set of categories (sub-populations) a new observation belongs, on the basis of a training set of data containing observations whose category membership is known. Examples are assigning a given email to the "spam" or "non-spam" class, and assigning a diagnosis to a given patient based on observed characteristics of the patient. Classification is an example of pattern recognition.
Given a population whose members each belong to one of a number of different sets or classes, a classification rule or classifier is a procedure by which the elements of the population set are each predicted to belong to one of the classes. A perfect classification is one for which every element in the population is assigned to the class it really belongs to. An imperfect classification is one in which some errors appear, and then statistical analysis must be applied to analyse the classification.
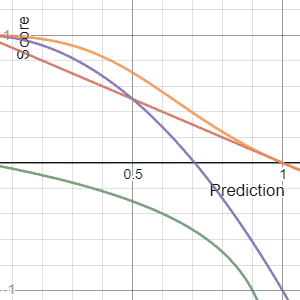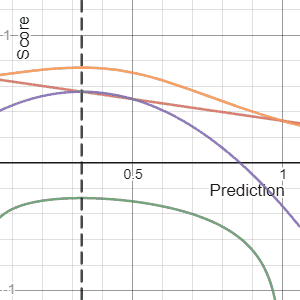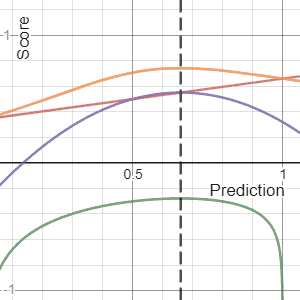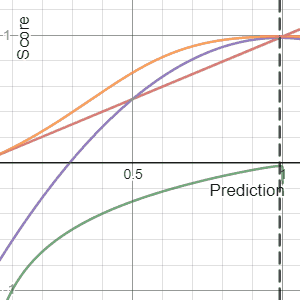
In decision theory, a score function, or scoring rule, measures the accuracy of probabilistic predictions. It is applicable to tasks in which predictions must assign probabilities to a set of mutually exclusive outcomes. The set of possible outcomes can be either binary or categorical in nature, and the probabilities assigned to this set of outcomes must sum to one. A score can be thought of as either a measure of the "calibration" of a set of probabilistic predictions, or as a "cost function" or "loss function".

Sensitivity and specificity are statistical measures of the performance of a binary classification test that are widely used in medicine:
In machine learning, multi-label classification and the strongly related problem of multi-output classification are variants of the classification problem where multiple labels may be assigned to each instance. Multi-label classification is a generalization of multiclass classification, which is the single-label problem of categorizing instances into precisely one of more than two classes; in the multi-label problem there is no constraint on how many of the classes the instance can be assigned to.
The Matthews correlation coefficient (MCC) or phi coefficient is used in machine learning as a measure of the quality of binary (two-class) classifications, introduced by biochemist Brian W. Matthews in 1975. The MCC is defined identically to Pearson's phi coefficient, introduced by Karl Pearson, also known as the Yule phi coefficient from its introduction by Udny Yule in 1912. Despite these antecedents which predate Matthews's use by several decades, the term MCC is widely used in the field of bioinformatics and machine learning.

In pattern recognition, information retrieval and classification, precision is the fraction of relevant instances among the retrieved instances, while recall is the fraction of the total amount of relevant instances that were actually retrieved. Both precision and recall are therefore based on an understanding and measure of relevance.
In machine learning, multiclass or multinomial classification is the problem of classifying instances into one of three or more classes.
Thompson sampling, named after William R. Thompson, is a heuristic for choosing actions that addresses the exploration-exploitation dilemma in the multi-armed bandit problem. It consists of choosing the action that maximizes the expected reward with respect to a randomly drawn belief.
In machine learning, a given algorithm is said to be fair, or to have fairness, if its results are independent of given variables, especially those considered sensitive, such as the traits of individuals which should not correlate with the outcome.





