Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers (arithmetic).
The history of mathematics deals with the origin of discoveries in mathematics and the mathematical methods and notation of the past. Before the modern age and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. From 3000 BC the Mesopotamian states of Sumer, Akkad and Assyria, followed closely by Ancient Egypt and the Levantine state of Ebla began using arithmetic, algebra and geometry for purposes of taxation, commerce, trade and also in the field of astronomy to record time and formulate calendars.
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
Pythagoras of Samos was an ancient Ionian Greek philosopher, polymath and the eponymous founder of Pythagoreanism. His political and religious teachings were well known in Magna Graecia and influenced the philosophies of Plato, Aristotle, and, through them, the West in general. Knowledge of his life is clouded by legend; modern scholars disagree regarding Pythagoras's education and influences, but they do agree that, around 530 BC, he travelled to Croton in southern Italy, where he founded a school in which initiates were sworn to secrecy and lived a communal, ascetic lifestyle.
Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans. Pythagoras established the first Pythagorean community in the ancient Greek colony of Kroton, in modern Calabria (Italy). Early Pythagorean communities spread throughout Magna Graecia.
In Euclidean geometry, Carnot's theorem states that the sum of the signed distances from the circumcenter D to the sides of an arbitrary triangle ABC is
In mathematics, a proof by infinite descent, also known as Fermat's method of descent, is a particular kind of proof by contradiction used to show that a statement cannot possibly hold for any number, by showing that if the statement were to hold for a number, then the same would be true for a smaller number, leading to an infinite descent and ultimately a contradiction. It is a method which relies on the well-ordering principle, and is often used to show that a given equation, such as a Diophantine equation, has no solutions.
Pseudomathematics, or mathematical crankery, is a mathematics-like activity that does not adhere to the framework of rigor of formal mathematical practice. Common areas of pseudomathematics are solutions of problems proved to be unsolvable or recognized as extremely hard by experts, as well as attempts to apply mathematics to non-quantifiable areas. A person engaging in pseudomathematics is called a pseudomathematician or a pseudomath. Pseudomathematics has equivalents in other scientific fields, and may overlap with other topics characterized as pseudoscience.
Abū’l-‘Abbās al-Faḍl ibn Ḥātim al-Nairīzī was a Persian mathematician and astronomer from Nayriz, now in Fars Province, Iran.
The problem in number theory known as "Fermat's Last Theorem" has repeatedly received attention in fiction and popular culture. It was proved by Andrew Wiles in 1994.
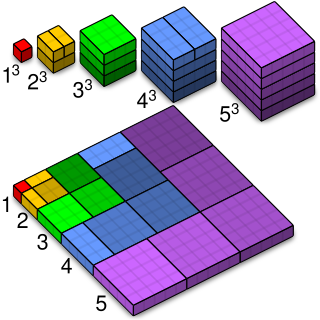
In mathematics, a proof without words is an illustration of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than formal or mathematically rigorous proofs due to their self-evident nature. When the diagram demonstrates a particular case of a general statement, to be a proof, it must be generalisable.
Mathematical beauty is the aesthetic pleasure derived from the abstractness, purity, simplicity, depth or orderliness of mathematics. Mathematicians may express this pleasure by describing mathematics as beautiful or describe mathematics as an art form, or, at a minimum, as a creative activity.
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c satisfy the equation an + bn = cn for any integer value of n greater than 2. The cases n = 1 and n = 2 have been known since antiquity to have infinitely many solutions.
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.
A Pythagorean tiling or two squares tessellation is a tiling of a Euclidean plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. Many proofs of the Pythagorean theorem are based on it, explaining its name. It is commonly used as a pattern for floor tiles. When used for this, it is also known as a hopscotch pattern or pinwheel pattern, but it should not be confused with the mathematical pinwheel tiling, an unrelated pattern.
Henry Perigal, Jr. FRAS MRI was a British stockbroker and amateur mathematician, known for his dissection-based proof of the Pythagorean theorem and for his unorthodox belief that the moon does not rotate.
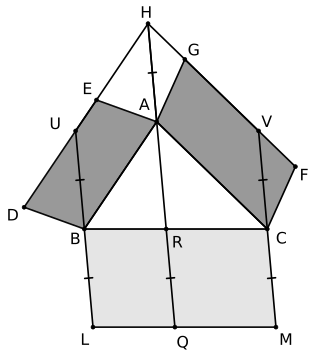
Pappus's area theorem describes the relationship between the areas of three parallelograms attached to three sides of an arbitrary triangle. The theorem, which can also be thought of as a generalization of the Pythagorean theorem, is named after the Greek mathematician Pappus of Alexandria, who discovered it.
Icons of Mathematics: An Exploration of Twenty Key Images is a book on elementary geometry for a popular audience. It was written by Roger B. Nelsen and Claudi Alsina, and published by the Mathematical Association of America in 2011 as volume 45 of their Dolciani Mathematical Expositions book series.
Street Musicians at the Door is an oil painting depicting members of a wealthy family interacting with two begging musicians at the door of their house. Dutch Golden Age artist Jacob Ochtervelt (1634–1682) painted it in Rotterdam in 1665, as an example of the "entrance hall painting", a genre he pioneered. It is in the collection of the Saint Louis Art Museum.
The eyeball theorem is a statement in elementary geometry about a property of a pair of disjoined circles.
Baugewerkeschule (Construction School) in Zittau, Germany
Minimalistic rendering
A high school student (presumably) wearing a red Pythagorean theorem t-shirt.
