
A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of both particles and waves, and quantum computing leverages this behavior using specialized hardware. Classical physics cannot explain the operation of these quantum devices, and a scalable quantum computer could perform some calculations exponentially faster than any modern "classical" computer. Theoretically a large-scale quantum computer could break some widely used encryption schemes and aid physicists in performing physical simulations; however, the current state of the art is largely experimental and impractical, with several obstacles to useful applications.
In quantum computing, Grover's algorithm, also known as the quantum search algorithm, is a quantum algorithm for unstructured search that finds with high probability the unique input to a black box function that produces a particular output value, using just evaluations of the function, where is the size of the function's domain. It was devised by Lov Grover in 1996.

Theoretical computer science is a subfield of computer science and mathematics that focuses on the abstract and mathematical foundations of computation.
In logic circuits, the Toffoli gate, also known as the CCNOT gate (“controlled-controlled-not”), invented by Tommaso Toffoli, is a CNOT gate with two control qubits and one target qubit. That is, the target qubit will be inverted if the first and second qubits are both 1. It is a universal reversible logic gate, which means that any classical reversible circuit can be constructed from Toffoli gates.

In quantum information theory, a quantum circuit is a model for quantum computation, similar to classical circuits, in which a computation is a sequence of quantum gates, measurements, initializations of qubits to known values, and possibly other actions. The minimum set of actions that a circuit needs to be able to perform on the qubits to enable quantum computation is known as DiVincenzo's criteria.
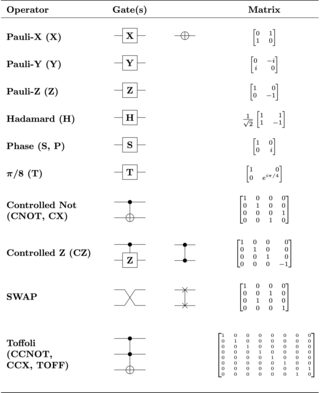
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate is a basic quantum circuit operating on a small number of qubits. Quantum logic gates are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.
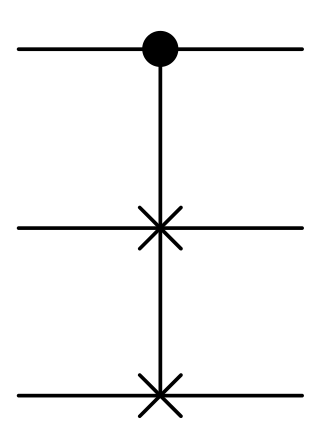
The Fredkin gate is a computational circuit suitable for reversible computing, invented by Edward Fredkin. It is universal, which means that any logical or arithmetic operation can be constructed entirely of Fredkin gates. The Fredkin gate is a circuit or device with three inputs and three outputs that transmits the first bit unchanged and swaps the last two bits if, and only if, the first bit is 1.
Quantum programming is the process of designing or assembling sequences of instructions, called quantum circuits, using gates, switches, and operators to manipulate a quantum system for a desired outcome or results of a given experiment. Quantum circuit algorithms can be implemented on integrated circuits, conducted with instrumentation, or written in a programming language for use with a quantum computer or a quantum processor.

Quantum neural networks are computational neural network models which are based on the principles of quantum mechanics. The first ideas on quantum neural computation were published independently in 1995 by Subhash Kak and Ron Chrisley, engaging with the theory of quantum mind, which posits that quantum effects play a role in cognitive function. However, typical research in quantum neural networks involves combining classical artificial neural network models with the advantages of quantum information in order to develop more efficient algorithms. One important motivation for these investigations is the difficulty to train classical neural networks, especially in big data applications. The hope is that features of quantum computing such as quantum parallelism or the effects of interference and entanglement can be used as resources. Since the technological implementation of a quantum computer is still in a premature stage, such quantum neural network models are mostly theoretical proposals that await their full implementation in physical experiments.
In quantum computing, the Gottesman–Knill theorem is a theoretical result by Daniel Gottesman and Emanuel Knill that states that stabilizer circuits–circuits that only consist of gates from the normalizer of the qubit Pauli group, also called Clifford group–can be perfectly simulated in polynomial time on a probabilistic classical computer. The Clifford group can be generated solely by using the controlled NOT, Hadamard, and phase gates ; and therefore stabilizer circuits can be constructed using only these gates.
Quantum complexity theory is the subfield of computational complexity theory that deals with complexity classes defined using quantum computers, a computational model based on quantum mechanics. It studies the hardness of computational problems in relation to these complexity classes, as well as the relationship between quantum complexity classes and classical complexity classes.
In quantum computing, the quantum Fourier transform (QFT) is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform. The quantum Fourier transform is a part of many quantum algorithms, notably Shor's algorithm for factoring and computing the discrete logarithm, the quantum phase estimation algorithm for estimating the eigenvalues of a unitary operator, and algorithms for the hidden subgroup problem. The quantum Fourier transform was discovered by Don Coppersmith. With small modifications to the QFT, it can also be used for performing fast integer arithmetic operations such as addition and multiplication.
Quantum optimization algorithms are quantum algorithms that are used to solve optimization problems. Mathematical optimization deals with finding the best solution to a problem from a set of possible solutions. Mostly, the optimization problem is formulated as a minimization problem, where one tries to minimize an error which depends on the solution: the optimal solution has the minimal error. Different optimization techniques are applied in various fields such as mechanics, economics and engineering, and as the complexity and amount of data involved rise, more efficient ways of solving optimization problems are needed. Quantum computing may allow problems which are not practically feasible on classical computers to be solved, or suggest a considerable speed up with respect to the best known classical algorithm.
Quantum counting algorithm is a quantum algorithm for efficiently counting the number of solutions for a given search problem. The algorithm is based on the quantum phase estimation algorithm and on Grover's search algorithm.
Quantum image processing (QIMP) is using quantum computing or quantum information processing to create and work with quantum images.
Open Quantum Assembly Language is a programming language designed for describing quantum circuits and algorithms for execution on quantum computers. It is designed to be an intermediate representation that can be used by higher-level compilers to communicate with quantum hardware, and allows for the description of a wide range of quantum operations, as well as classical feed-forward flow control based on measurement outcomes.
Quil is a quantum instruction set architecture that first introduced a shared quantum/classical memory model. It was introduced by Robert Smith, Michael Curtis, and William Zeng in A Practical Quantum Instruction Set Architecture. Many quantum algorithms require a shared memory architecture. Quil is being developed for the superconducting quantum processors developed by Rigetti Computing through the Forest quantum programming API. A Python library called pyQuil was introduced to develop Quil programs with higher level constructs. A Quil backend is also supported by other quantum programming environments.
Q# is a domain-specific programming language used for expressing quantum algorithms. It was initially released to the public by Microsoft as part of the Quantum Development Kit.
This glossary of quantum computing is a list of definitions of terms and concepts used in quantum computing, its sub-disciplines, and related fields.
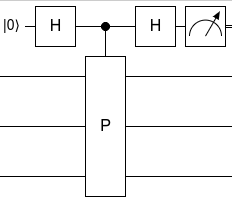
In quantum computing, phase kickback refers to the fact that controlled operations have effects on their controls, in addition to on their targets, and that these effects correspond to phasing operations. The phase of one qubit is effectively transferred to another qubit during a controlled operation, creating entanglement and computational advantages that enable various popular quantum algorithms and protocols.






