
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid phases which arise from electromagnetic forces between atoms. More generally, the subject deals with "condensed" phases of matter: systems of many constituents with strong interactions between them. More exotic condensed phases include the superconducting phase exhibited by certain materials at low temperature, the ferromagnetic and antiferromagnetic phases of spins on crystal lattices of atoms, and the Bose–Einstein condensate found in ultracold atomic systems. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theories to develop mathematical models.
The quantum Hall effect is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance Rxy exhibits steps that take on the quantized values

In particle physics, a magnetic monopole is a hypothetical elementary particle that is an isolated magnet with only one magnetic pole. A magnetic monopole would have a net north or south "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring theories, which predict their existence. The known elementary particles that have electric charge are electric monopoles.

In physics, the Kondo effect describes the scattering of conduction electrons in a metal due to magnetic impurities, resulting in a characteristic change i.e. a minimum in electrical resistivity with temperature. The cause of the effect was first explained by Jun Kondo, who applied third-order perturbation theory to the problem to account for scattering of s-orbital conduction electrons off d-orbital electrons localized at impurities. Kondo's calculation predicted that the scattering rate and the resulting part of the resistivity should increase logarithmically as the temperature approaches 0 K. Experiments in the 1960s by Myriam Sarachik at Bell Laboratories provided the first data that confirmed the Kondo effect. Extended to a lattice of magnetic impurities, the Kondo effect likely explains the formation of heavy fermions and Kondo insulators in intermetallic compounds, especially those involving rare earth elements such as cerium, praseodymium, and ytterbium, and actinide elements such as uranium. The Kondo effect has also been observed in quantum dot systems.
In physics, an anyon is a type of quasiparticle that occurs only in two-dimensional systems, with properties much less restricted than the two kinds of standard elementary particles, fermions and bosons. In general, the operation of exchanging two identical particles, although it may cause a global phase shift, cannot affect observables. Anyons are generally classified as abelian or non-abelian. Abelian anyons play a major role in the fractional quantum Hall effect. Non-abelian anyons have not been definitively detected, although this is an active area of research.
The fractional quantum Hall effect (FQHE) is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of . It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations have a fractional elementary charge and possibly also fractional statistics. The 1998 Nobel Prize in Physics was awarded to Robert Laughlin, Horst Störmer, and Daniel Tsui "for their discovery of a new form of quantum fluid with fractionally charged excitations" Laughlin's explanation only applies to fillings where is an odd integer. The microscopic origin of the FQHE is a major research topic in condensed matter physics.

In condensed matter physics, Hofstadter's butterfly is a graph of the spectral properties of non-interacting two-dimensional electrons in a perpendicular magnetic field in a lattice. The fractal, self-similar nature of the spectrum was discovered in the 1976 Ph.D. work of Douglas Hofstadter and is one of the early examples of modern scientific data visualization. The name reflects the fact that, as Hofstadter wrote, "the large gaps [in the graph] form a very striking pattern somewhat resembling a butterfly."

In physics, topological order is a kind of order in the zero-temperature phase of matter. Macroscopically, topological order is defined and described by robust ground state degeneracy and quantized non-Abelian geometric phases of degenerate ground states. Microscopically, topological orders correspond to patterns of long-range quantum entanglement. States with different topological orders cannot change into each other without a phase transition.

A Majorana fermion, also referred to as a Majorana particle, is a fermion that is its own antiparticle. They were hypothesised by Ettore Majorana in 1937. The term is sometimes used in opposition to a Dirac fermion, which describes fermions that are not their own antiparticles.
The quantum spin Hall state is a state of matter proposed to exist in special, two-dimensional semiconductors that have a quantized spin-Hall conductance and a vanishing charge-Hall conductance. The quantum spin Hall state of matter is the cousin of the integer quantum Hall state, and that does not require the application of a large magnetic field. The quantum spin Hall state does not break charge conservation symmetry and spin- conservation symmetry.
A composite fermion is the topological bound state of an electron and an even number of quantized vortices, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect, but subsequently took on a life of their own, exhibiting many other consequences and phenomena.

A topological insulator is a material that behaves as an insulator in its interior but whose surface contains conducting states, meaning that electrons can only move along the surface of the material. Topological insulators have non-trivial symmetry-protected topological order; however, having a conducting surface is not unique to topological insulators, since ordinary band insulators can also support conductive surface states. What is special about topological insulators is that their surface states are symmetry-protected Dirac fermions by particle number conservation and time-reversal symmetry. In two-dimensional (2D) systems, this ordering is analogous to a conventional electron gas subject to a strong external magnetic field causing electronic excitation gap in the sample bulk and metallic conduction at the boundaries or surfaces.
In quantum mechanics, fractionalization is the phenomenon whereby the quasiparticles of a system cannot be constructed as combinations of its elementary constituents. One of the earliest and most prominent examples is the fractional quantum Hall effect, where the constituent particles are electrons but the quasiparticles carry fractions of the electron charge. Fractionalization can be understood as deconfinement of quasiparticles that together are viewed as comprising the elementary constituents. In the case of spin–charge separation, for example, the electron can be viewed as a bound state of a 'spinon' and a 'chargon', which under certain conditions can become free to move separately.

Shoucheng Zhang was a Chinese-American physicist who was the JG Jackson and CJ Wood professor of physics at Stanford University. He was a condensed matter theorist known for his work on topological insulators, the quantum Hall effect, the quantum spin Hall effect, spintronics, and high-temperature superconductivity. According to the National Academy of Sciences:
He discovered a new state of matter called topological insulator in which electrons can conduct along the edge without dissipation, enabling a new generation of electronic devices with much lower power consumption. For this ground breaking work he received numerous international awards, including the Buckley Prize, the Dirac Medal and Prize, the Europhysics Prize, the Physics Frontiers Prize and the Benjamin Franklin Medal.
Symmetry-protected topological (SPT) order is a kind of order in zero-temperature quantum-mechanical states of matter that have a symmetry and a finite energy gap.

Xue Qikun is a Chinese physicist. He is a professor of Tsinghua University, Beijing. He has done much work in Condensed Matter Physics, especially on superconductors and topological insulators. In 2013, Xue was the first to achieve the quantum anomalous Hall effect (QAHE), an unusual orderly motion of electrons in a conductor, in his laboratory at Tsinghua University. Xue is a member of the Chinese Academy of Sciences, vice president for research of Tsinghua University, and director of State Key Lab of Quantum Physics. In 2016, he was one of the first recipients of the new Chinese Future Science Award for experimental discovery of high-temperature superconductivity at material interfaces and the QAHE. This award has been described as "China's Nobel Prize".
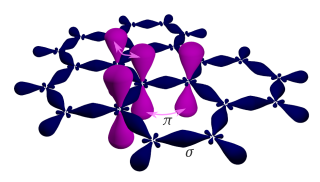
Graphene is a semimetal whose conduction and valence bands meet at the Dirac points, which are six locations in momentum space, the vertices of its hexagonal Brillouin zone, divided into two non-equivalent sets of three points. The two sets are labeled K and K'. The sets give graphene a valley degeneracy of gv = 2. By contrast, for traditional semiconductors the primary point of interest is generally Γ, where momentum is zero. Four electronic properties separate it from other condensed matter systems.
The term Dirac matter refers to a class of condensed matter systems which can be effectively described by the Dirac equation. Even though the Dirac equation itself was formulated for fermions, the quasi-particles present within Dirac matter can be of any statistics. As a consequence, Dirac matter can be distinguished in fermionic, bosonic or anyonic Dirac matter. Prominent examples of Dirac matter are Graphene, topological insulators, Dirac semimetals, Weyl semimetals, various high-temperature superconductors with -wave pairing and liquid Helium-3. The effective theory of such systems is classified by a specific choice of the Dirac mass, the Dirac velocity, the Dirac matrices and the space-time curvature. The universal treatment of the class of Dirac matter in terms of an effective theory leads to a common features with respect to the density of states, the heat capacity and impurity scattering.
Magnetic topological insulators are three dimensional magnetic materials with a non-trivial topological index protected by a symmetry other than time-reversal. In contrast with a non-magnetic topological insulator, a magnetic topological insulator can have naturally gapped surface states as long as the quantizing symmetry is broken at the surface. These gapped surfaces exhibit a topologically protected half-quantized surface anomalous Hall conductivity perpendicular to the surface. The sign of the half-quantized surface anomalous Hall conductivity depends on the specific surface termination.
Photonic topological insulators are artificial electromagnetic materials that support topologically non-trivial, unidirectional states of light. Photonic topological phases are classical electromagnetic wave analogues of electronic topological phases studied in condensed matter physics. Similar to their electronic counterparts, they, can provide robust unidirectional channels for light propagation.









