 | Look up Radius or radius in Wiktionary, the free dictionary. |
A radius is a straight line or distance from the center to the edge of a curve.
Radius may also refer to:
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for the diameter of a sphere.
In general, a node is a localized swelling or a point of intersection.
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians.
Network, networking and networked may refer to:
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
Vertex means the "top", or the highest geometric point of something, usually a curved surface or line, or a point where any two geometric sides or edges meet regardless of elevation; as opposed to an apex which is frequently a highest angular point such as possessed by a triangle, pyramid, or cone. It may refer to:
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
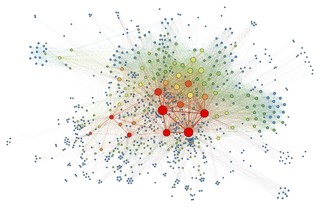
Force-directed graph drawing algorithms are a class of algorithms for drawing graphs in an aesthetically-pleasing way. Their purpose is to position the nodes of a graph in two-dimensional or three-dimensional space so that all the edges are of more or less equal length and there are as few crossing edges as possible, by assigning forces among the set of edges and the set of nodes, based on their relative positions, and then using these forces either to simulate the motion of the edges and nodes or to minimize their energy.
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance or shortest-path distance. Notice that there may be more than one shortest path between two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected components, then conventionally the distance is defined as infinite.
In classical geometry, a radius of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin radius, meaning ray but also the spoke of a chariot wheel. The plural of radius can be either radii or the conventional English plural radiuses. The typical abbreviation and mathematical variable name for radius is R or r. By extension, the diameter D is defined as twice the radius:
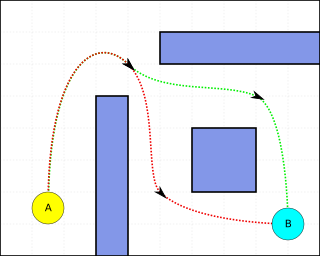
Pathfinding or pathing is the plotting, by a computer application, of the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra's algorithm for finding the shortest path on a weighted graph.
Two-dimensional Euclidean space or simply two-dimensional space is a geometric setting in which two values are required to determine the position of an element on the plane. The set of pairs of real numbers with appropriate structure often serves as the canonical example of a Euclidean plane, the two-dimensional Euclidean space; for a generalization of the concept, see dimension. Two-dimensional space can be seen as a projection of the physical universe onto a plane. Usually, it is thought of as a Euclidean space and the two dimensions are called length and width.
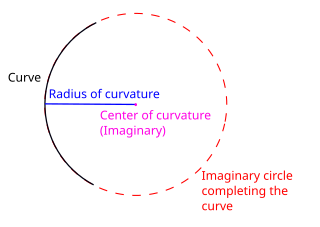
In differential geometry, the radius of curvature, R, is the reciprocal of the curvature. For a curve, it equals the radius of the circular arc which best approximates the curve at that point. For surfaces, the radius of curvature is the radius of a circle that best fits a normal section or combinations thereof.
The minimum railway curve radius is the shortest allowable design radius for the centerline of railway tracks under a particular set of conditions. It has an important bearing on construction costs and operating costs and, in combination with superelevation in the case of train tracks, determines the maximum safe speed of a curve. The minimum radius of a curve is one parameter in the design of railway vehicles as well as trams; monorails and automated guideways are also subject to a minimum radius.
A radial tree, or radial map, is a method of displaying a tree structure in a way that expands outwards, radially. It is one of many ways to visually display a tree, with examples extending back to the early 20th century. In use, it is a type of information graphic.
In technical applications of 3D computer graphics (CAx) such as computer-aided design and computer-aided manufacturing, surfaces are one way of representing objects. The other ways are wireframe and solids. Point clouds are also sometimes used as temporary ways to represent an object, with the goal of using the points to create one or more of the three permanent representations.
The stretched grid method (SGM) is a numerical technique for finding approximate solutions of various mathematical and engineering problems that can be related to an elastic grid behavior. In particular, meteorologists use the stretched grid method for weather prediction and engineers use the stretched grid method to design tents and other tensile structures.
A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is a special type of spatial network where (1) latent coordinates of nodes are sprinkled according to a probability density function into a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric. A HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.