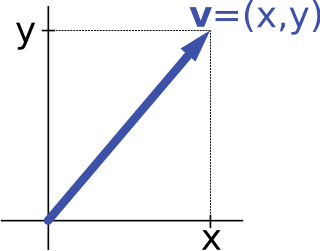 | This article has multiple issues. Please help improve it or discuss these issues on the talk page . (Learn how and when to remove these template messages) (Learn how and when to remove this template message)
|
Range rate defines a signed scalar value describing the time rate of change of the range (distance) between two locations.
Given a differentiable vector defining the instantaneous position of a target relative to an observer.
Let
| (1) |
with , the instantaneous velocity of the target with respect to the observer.
The magnitude of the position vector is defined as
| (2) |
The quantity range rate is the time derivative of the magnitude (norm) of , expressed as
| (3) |
Evaluating the derivative of the right-hand-side
using ( 1 ) the expression becomes
Since [1]
With
The range rate is simply defined as
the projection of the observer to target velocity vector onto the unit vector.
A singularity exists for coincident observer target, i.e. . In this case, range rate does not exist as .
In quantum mechanics, bra–ket notation, or Dirac notation, is ubiquitous. The notation uses the angle brackets, "" and "", and a vertical bar "", to construct "bras" and "kets".
In mathematics, an inner product space or a Hausdorff pre-Hilbert space is a vector space with a binary operation called an inner product. This operation associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors, often denoted using angle brackets. Inner products allow the rigorous introduction of intuitive geometrical notions, such as the length of a vector or the angle between two vectors. They also provide the means of defining orthogonality between vectors. Inner product spaces generalize Euclidean spaces to vector spaces of any dimension, and are studied in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.
In mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by potential forces, with that of the total potential energy of the system. Mathematically, the theorem states
In mathematics, the Cauchy–Schwarz inequality, also known as the Cauchy–Bunyakovsky–Schwarz inequality, is a useful inequality in many mathematical fields, such as linear algebra, analysis, probability theory, vector algebra and other areas. It is considered to be one of the most important inequalities in all of mathematics.
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance, and orientation. Every non-trivial rotation is determined by its axis of rotation and its angle of rotation. Composing two rotations results in another rotation; every rotation has a unique inverse rotation; and the identity map satisfies the definition of a rotation. Owing to the above properties, the set of all rotations is a group under composition. Rotations are not commutative, making it a nonabelian group. Moreover, the rotation group has a natural structure as a manifold for which the group operations are smoothly differentiable; so it is in fact a Lie group. It is compact and has dimension 3.
In mathematics, particularly in linear algebra, a skew-symmetricmatrix is a square matrix whose transpose equals its negative. That is, it satisfies the condition
In mathematics, a linear form is a linear map from a vector space to its field of scalars.
In physics, an operator is a function over a space of physical states onto another space of physical states. The simplest example of the utility of operators is the study of symmetry. Because of this, they are very useful tools in classical mechanics. Operators are even more important in quantum mechanics, where they form an intrinsic part of the formulation of the theory.
In mathematics, the Hodge star operator or Hodge star is a linear map defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. Applying the operator to an element of the algebra produces the Hodge dual of the element. This map was introduced by W. V. D. Hodge.
Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and the Euclidean space by methods of differential and integral calculus.
In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a continuous, differentiable curve in three-dimensional Euclidean space ℝ3, or the geometric properties of the curve itself irrespective of any motion. More specifically, the formulas describe the derivatives of the so-called tangent, normal, and binormal unit vectors in terms of each other. The formulas are named after the two French mathematicians who independently discovered them: Jean Frédéric Frenet, in his thesis of 1847, and Joseph Alfred Serret in 1851. Vector notation and linear algebra currently used to write these formulas were not yet in use at the time of their discovery.
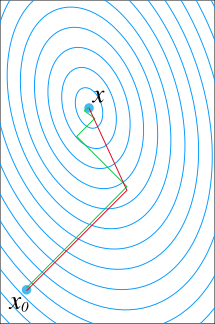
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-definite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.
A vector-valued function, also referred to as a vector function, is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors. The input of a vector-valued function could be a scalar or a vector ; the dimension of the domain is not defined by the dimension of the range.
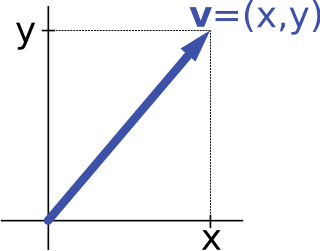
Vector notation is a commonly used mathematical notation for working with mathematical vectors, which may be geometric vectors or members of vector spaces.
In physics and engineering, mass flux is the rate of mass flow, . The common symbols are j, J, q, Q, φ, or Φ, sometimes with subscript m to indicate mass is the flowing quantity. Its SI units are kg m-2 s−1. Mass flux can also refer to an alternate form of flux in Fick's law that includes the molecular mass, or in Darcy's law that includes the mass density.
This article derives the main properties of rotations in 3-dimensional space.
In pure and applied mathematics, particularly quantum mechanics and computer graphics and their applications, a spherical basis is the basis used to express spherical tensors. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions.
In quantum mechanics, a translation operator is defined as an operator which shifts particles and fields by a certain amount in a certain direction.
Magnetic resonance is a quantum mechanical resonant effect that can appear when a magnetic dipole is exposed to a static magnetic field and perturbed with another, oscillating electromagnetic field. Due to the static field, the dipole can assume a number of discrete energy eigenstates, depending on the value of its angular momentum quantum number. The oscillating field can then make the dipole transit between its energy states with a certain probability and at a certain rate. The overall transition probability will depend on the field's frequency and the rate will depend on its amplitude. When the frequency of that field leads to the maximum possible transition probability between two states, a magnetic resonance has been achieved. In that case, the energy of the photons composing the oscillating field matches the energy difference between said states. If the dipole is tickled with a field oscillating far from resonance, it is unlikely to transition. That is analogous to other resonant effects, such as with the forced harmonic oscillator. The periodic transition between the different states is called Rabi cycle and the rate at which that happens is called Rabi frequency. The Rabi frequency should not be confused with the field's own frequency. Since many atomic nuclei species can behave as a magnetic dipole, this resonance technique is the basis of nuclear magnetic resonance, including nuclear magnetic resonance imaging and nuclear magnetic resonance spectroscopy.
