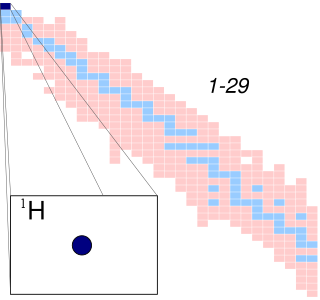
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe.
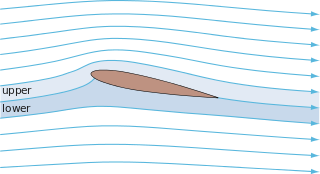
In fluid dynamics, potential flow is the ideal flow pattern of an inviscid fluid. Potential flows are described and determined by mathematical methods.
The Klein–Gordon equation is a relativistic wave equation, related to the Schrödinger equation. It is second-order in space and time and manifestly Lorentz-covariant. It is a quantized version of the relativistic energy–momentum relation . Its solutions include a quantum scalar or pseudoscalar field, a field whose quanta are spinless particles. Its theoretical relevance is similar to that of the Dirac equation. Electromagnetic interactions can be incorporated, forming the topic of scalar electrodynamics, but because common spinless particles like the pions are unstable and also experience the strong interaction the practical utility is limited.

In physics, the Rabi cycle is the cyclic behaviour of a two-level quantum system in the presence of an oscillatory driving field. A great variety of physical processes belonging to the areas of quantum computing, condensed matter, atomic and molecular physics, and nuclear and particle physics can be conveniently studied in terms of two-level quantum mechanical systems, and exhibit Rabi flopping when coupled to an optical driving field. The effect is important in quantum optics, magnetic resonance and quantum computing, and is named after Isidor Isaac Rabi.
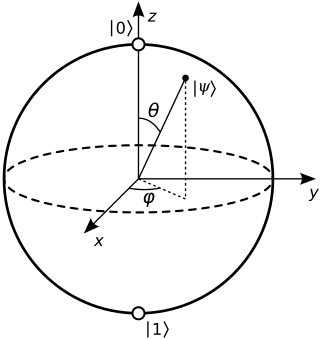
In quantum mechanics and computing, the Bloch sphere is a geometrical representation of the pure state space of a two-level quantum mechanical system (qubit), named after the physicist Felix Bloch.
In theoretical physics, the Wess–Zumino model has become the first known example of an interacting four-dimensional quantum field theory with linearly realised supersymmetry. In 1974, Julius Wess and Bruno Zumino studied, using modern terminology, dynamics of a single chiral superfield whose cubic superpotential leads to a renormalizable theory.

In classical mechanics, Routh's procedure or Routhian mechanics is a hybrid formulation of Lagrangian mechanics and Hamiltonian mechanics developed by Edward John Routh. Correspondingly, the Routhian is the function which replaces both the Lagrangian and Hamiltonian functions. Routhian mechanics is equivalent to Lagrangian mechanics and Hamiltonian mechanics, and introduces no new physics. It offers an alternative way to solve mechanical problems.
Hill's spherical vortex is an exact solution of the Euler equations that is commonly used to model a vortex ring. The solution is also used to model the velocity distribution inside a spherical drop of one fluid moving at a constant velocity through another fluid at small Reynolds number. The vortex is named after Micaiah John Muller Hill who discovered the exact solution in 1894. The two-dimensional analogue of this vortex is the Lamb–Chaplygin dipole.
In quantum mechanics, the angular momentum operator is one of several related operators analogous to classical angular momentum. The angular momentum operator plays a central role in the theory of atomic and molecular physics and other quantum problems involving rotational symmetry. Such an operator is applied to a mathematical representation of the physical state of a system and yields an angular momentum value if the state has a definite value for it. In both classical and quantum mechanical systems, angular momentum is one of the three fundamental properties of motion.
In abstract algebraic logic, a branch of mathematical logic, the Leibniz operator is a tool used to classify deductive systems, which have a precise technical definition and capture a large number of logics. The Leibniz operator was introduced by Wim Blok and Don Pigozzi, two of the founders of the field, as a means to abstract the well-known Lindenbaum–Tarski process, that leads to the association of Boolean algebras to classical propositional calculus, and make it applicable to as wide a variety of sentential logics as possible. It is an operator that assigns to a given theory of a given sentential logic, perceived as a term algebra with a consequence operation on its universe, the largest congruence on the algebra that is compatible with the theory.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.
In general relativity, the Vaidya metric describes the non-empty external spacetime of a spherically symmetric and nonrotating star which is either emitting or absorbing null dusts. It is named after the Indian physicist Prahalad Chunnilal Vaidya and constitutes the simplest non-static generalization of the non-radiative Schwarzschild solution to Einstein's field equation, and therefore is also called the "radiating(shining) Schwarzschild metric".
The Bowring series of the transverse mercator published in 1989 by Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy.
Calculations in the Newman–Penrose (NP) formalism of general relativity normally begin with the construction of a complex null tetrad, where is a pair of real null vectors and is a pair of complex null vectors. These tetrad vectors respect the following normalization and metric conditions assuming the spacetime signature
In physics, the distorted Schwarzschild metric is the metric of a standard/isolated Schwarzschild spacetime exposed in external fields. In numerical simulation, the Schwarzschild metric can be distorted by almost arbitrary kinds of external energy–momentum distribution. However, in exact analysis, the mature method to distort the standard Schwarzschild metric is restricted to the framework of Weyl metrics.
Conformastatic spacetimes refer to a special class of static solutions to Einstein's equation in general relativity.
In pure and applied mathematics, quantum mechanics and computer graphics, a tensor operator generalizes the notion of operators which are scalars and vectors. A special class of these are spherical tensor operators which apply the notion of the spherical basis and spherical harmonics. The spherical basis closely relates to the description of angular momentum in quantum mechanics and spherical harmonic functions. The coordinate-free generalization of a tensor operator is known as a representation operator.
Pure inductive logic (PIL) is the area of mathematical logic concerned with the philosophical and mathematical foundations of probabilistic inductive reasoning. It combines classical predicate logic and probability theory. Probability values are assigned to sentences of a first-order relational language to represent degrees of belief that should be held by a rational agent. Conditional probability values represent degrees of belief based on the assumption of some received evidence.










































