In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic at all finite points over the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function f(z) has a root at w, then f(z)/(z−w), taking the limit value at w, is an entire function. On the other hand, neither the natural logarithm nor the square root is an entire function, nor can they be continued analytically to an entire function.
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures, through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point.
In mathematics, a power series is an infinite series of the form
In mathematics, a formal power series is a generalization of a polynomial, where the number of terms is allowed to be infinite; this implies giving up the possibility of replacing the variable in the polynomial with an arbitrary number. Thus a formal power series differs from a polynomial in that it may have infinitely many terms, and differs from a power series, whose variables can take on numerical values. One way to view a formal power series is as an infinite ordered sequence of numbers. In this case, the powers of the variable are used only to indicate the order of the coefficients, so that the coefficient of is the fifth term in the sequence. In combinatorics, formal power series provide representations of numerical sequences and of multisets, and for instance allow concise expressions for recursively defined sequences regardless of whether the recursion can be explicitly solved; this is known as the method of generating functions. More generally, formal power series can include series with any finite number of variables, and with coefficients in an arbitrary ring. Formal power series can be created from Taylor polynomials using formal moduli.
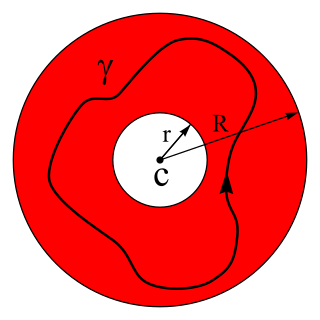
In mathematics, the radius of convergence of a power series is the radius of the largest disk in which the series converges. It is either a non-negative real number or . When it is positive, the power series converges absolutely and uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges.
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which it is initially defined becomes divergent.
In mathematics, a rational function is any function which can be defined by a rational fraction, i.e. an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field K. In this case, one speaks of a rational function and a rational fraction over K. The values of the variables may be taken in any field L containing K. Then the domain of the function is the set of the values of the variables for which the denominator is not zero and the codomain is L.
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit.
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original function. The function being expanded may be complex in general. Multipole expansions are very frequently used in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space.

In mathematics, the Riesz function is an entire function defined by Marcel Riesz in connection with the Riemann hypothesis, by means of the power series
In mathematics, the root test is a criterion for the convergence of an infinite series. It depends on the quantity
In mathematics, a series is the sum of the terms of an infinite sequence of numbers.
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt. It is an example of an important arithmetic function that is neither multiplicative nor additive.
In mathematics, the Cauchy condensation test, named after Augustin-Louis Cauchy, is a standard convergence test for infinite series. For a non-increasing sequence of non-negative real numbers, the series converges if and only if the "condensed" series converges. Moreover, if they converge, the sum of the condensed series is no more than twice as large as the sum of the original.
In complex analysis, a partial fraction expansion is a way of writing a meromorphic function f(z) as an infinite sum of rational functions and polynomials. When f(z) is a rational function, this reduces to the usual method of partial fractions.
In probability theory and directional statistics, a wrapped probability distribution is a continuous probability distribution that describes data points that lie on a unit n-sphere. In one dimension, a wrapped distribution will consist of points on the unit circle. If φ is a random variate in the interval (-∞,∞) with probability density function p(φ), then z = e i φ will be a circular variable distributed according to the wrapped distribution pzw(z) and θ=arg(z) will be an angular variable in the interval (-π,π ] distributed according to the wrapped distribution pw.
In mathematics, a multisection of a power series is a new power series composed of equally spaced terms extracted unaltered from the original series. Formally, if one is given a power series