The Riemann–Roch theorem is an important theorem in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles. It relates the complex analysis of a connected compact Riemann surface with the surface's purely topological genus g, in a way that can be carried over into purely algebraic settings.

In algebraic geometry, a projective variety over an algebraically closed field k is a subset of some projective n-space over k that is the zero-locus of some finite family of homogeneous polynomials of n + 1 variables with coefficients in k, that generate a prime ideal, the defining ideal of the variety. Equivalently, an algebraic variety is projective if it can be embedded as a Zariski closed subvariety of .
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a class of sheaves closely linked to the geometric properties of the underlying space. The definition of coherent sheaves is made with reference to a sheaf of rings that codifies this geometric information.
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.
In mathematics, the canonical bundle of a non-singular algebraic variety of dimension over a field is the line bundle , which is the nth exterior power of the cotangent bundle Ω on V.
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold into projective space. An ample line bundle is one such that some positive power is very ample. Globally generated sheaves are those with enough sections to define a morphism to projective space.
In algebraic geometry, the Kodaira dimensionκ(X) measures the size of the canonical model of a projective variety X.
In mathematics, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch, Bernhard Riemann, and Gustav Roch, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem for complex algebraic varieties of all dimensions. It was the first successful generalisation of the classical Riemann–Roch theorem on Riemann surfaces to all higher dimensions, and paved the way to the Grothendieck–Hirzebruch–Riemann–Roch theorem proved about three years later.
In algebraic geometry, a Fano variety, introduced by Gino Fano in, is a complete variety X whose anticanonical bundle KX* is ample. In this definition, one could assume that X is smooth over a field, but the minimal model program has also led to the study of Fano varieties with various types of singularities, such as terminal or klt singularities.
In mathematics, the Riemann–Roch theorem for surfaces describes the dimension of linear systems on an algebraic surface. The classical form of it was first given by Castelnuovo, after preliminary versions of it were found by Noether (1886) and Enriques (1894). The sheaf-theoretic version is due to Hirzebruch.
In algebraic geometry, the Chow groups of an algebraic variety over any field are algebro-geometric analogs of the homology of a topological space. The elements of the Chow group are formed out of subvarieties in a similar way to how simplicial or cellular homology groups are formed out of subcomplexes. When the variety is smooth, the Chow groups can be interpreted as cohomology groups and have a multiplication called the intersection product. The Chow groups carry rich information about an algebraic variety, and they are correspondingly hard to compute in general.
In mathematics, Arakelov theory is an approach to Diophantine geometry, named for Suren Arakelov. It is used to study Diophantine equations in higher dimensions.
In mathematics, a stable vector bundle is a vector bundle that is stable in the sense of geometric invariant theory. Any holomorphic vector bundle may be built from stable ones using Harder-Narasimhan filtration. Stable bundles were defined by David Mumford in Mumford (1963) and later built upon by David Gieseker, Fedor Bogomolov, Thomas Bridgeland and many others.
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaf cohomology is a technique for producing functions with specified properties. Many geometric questions can be formulated as questions about the existence of sections of line bundles or of more general coherent sheaves; such sections can be viewed as generalized functions. Cohomology provides computable tools for producing sections, or explaining why they do not exist. It also provides invariants to distinguish one algebraic variety from another.
Projective space plays a central role in algebraic geometry. The aim of this article is to define the notion in terms of abstract algebraic geometry and to describe some basic uses of projective space.
This is a glossary of algebraic geometry.
The Annals of Mathematics is a mathematical journal published every two months by Princeton University and the Institute for Advanced Study.

In computing, a Digital Object Identifier or DOI is a persistent identifier or handle used to identify objects uniquely, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.
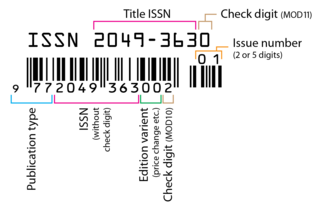
An International Standard Serial Number (ISSN) is an eight-digit serial number used to uniquely identify a serial publication, such as a magazine. The ISSN is especially helpful in distinguishing between serials with the same title. ISSN are used in ordering, cataloging, interlibrary loans, and other practices in connection with serial literature.










