Related Research Articles
Passive management is an investing strategy that tracks a market-weighted index or portfolio. Passive management is most common on the equity market, where index funds track a stock market index, but it is becoming more common in other investment types, including bonds, commodities and hedge funds.

In finance, the capital asset pricing model (CAPM) is a model used to determine a theoretically appropriate required rate of return of an asset, to make decisions about adding assets to a well-diversified portfolio.
Harry Max Markowitz was an American economist who received the 1989 John von Neumann Theory Prize and the 1990 Nobel Memorial Prize in Economic Sciences.
Modern portfolio theory (MPT), or mean-variance analysis, is a mathematical framework for assembling a portfolio of assets such that the expected return is maximized for a given level of risk. It is a formalization and extension of diversification in investing, the idea that owning different kinds of financial assets is less risky than owning only one type. Its key insight is that an asset's risk and return should not be assessed by itself, but by how it contributes to a portfolio's overall risk and return. The variance of return is used as a measure of risk, because it is tractable when assets are combined into portfolios. Often, the historical variance and covariance of returns is used as a proxy for the forward-looking versions of these quantities, but other, more sophisticated methods are available.
In finance, the beta is a statistic that measures the expected increase or decrease of an individual stock price in proportion to movements of the stock market as a whole. Beta can be used to indicate the contribution of an individual asset to the market risk of a portfolio when it is added in small quantity. It refers to an asset's non-diversifiable risk, systematic risk, or market risk. Beta is not a measure of idiosyncratic risk.
In finance, a portfolio is a collection of investments.
Equity risk is "the financial risk involved in holding equity in a particular investment." Equity risk is a type of market risk that applies to investing in shares. The market price of stocks fluctuates all the time, depending on supply and demand. The risk of losing money due to a reduction in the market price of shares is known as equity risk.
Investment management is the professional asset management of various securities, including shareholdings, bonds, and other assets, such as real estate, to meet specified investment goals for the benefit of investors. Investors may be institutions, such as insurance companies, pension funds, corporations, charities, educational establishments, or private investors, either directly via investment contracts/mandates or via collective investment schemes like mutual funds, exchange-traded funds, or Real estate investment trusts.

Asset allocation is the implementation of an investment strategy that attempts to balance risk versus reward by adjusting the percentage of each asset in an investment portfolio according to the investor's risk tolerance, goals and investment time frame. The focus is on the characteristics of the overall portfolio. Such a strategy contrasts with an approach that focuses on individual assets.
The following outline is provided as an overview of and topical guide to finance:
Asset location (AL) is a term used in personal finance to refer to how investors distribute their investments across savings vehicles including taxable accounts, tax-exempt accounts, tax-deferred accounts, trust accounts, variable life insurance policies, foundations, and onshore vs. offshore accounts.
In finance, the Black–Litterman model is a mathematical model for portfolio allocation developed in 1990 at Goldman Sachs by Fischer Black and Robert Litterman, and published in 1992. It seeks to overcome problems that institutional investors have encountered in applying modern portfolio theory in practice. The model starts with an asset allocation based on the equilibrium assumption and then modifies that allocation by taking into account the opinion of the investor regarding future asset performance.
Risk parity is an approach to investment management which focuses on allocation of risk, usually defined as volatility, rather than allocation of capital. The risk parity approach asserts that when asset allocations are adjusted to the same risk level, the risk parity portfolio can achieve a higher Sharpe ratio and can be more resistant to market downturns than the traditional portfolio. Risk parity is vulnerable to significant shifts in correlation regimes, such as observed in Q1 2020, which led to the significant underperformance of risk-parity funds in the Covid-19 sell-off.
Goals-Based Investing or Goal-Driven Investing is the use of financial markets to fund goals within a specified period of time. Traditional portfolio construction balances expected portfolio variance with return and uses a risk aversion metric to select the optimal mix of investments. By contrast, GBI optimizes an investment mix to minimize the probability of failing to achieve a minimum wealth level within a set period of time.
Maslowian portfolio theory (MaPT) creates a normative portfolio theory based on human needs as described by Abraham Maslow. It is in general agreement with behavioral portfolio theory, and is explained in Maslowian Portfolio Theory: An alternative formulation of the Behavioural Portfolio Theory, and was first observed in Behavioural Finance and Decision Making in Financial Markets.

Portfolio optimization is the process of selecting an optimal portfolio, out of a set of considered portfolios, according to some objective. The objective typically maximizes factors such as expected return, and minimizes costs like financial risk, resulting in a multi-objective optimization problem. Factors being considered may range from tangible to intangible.
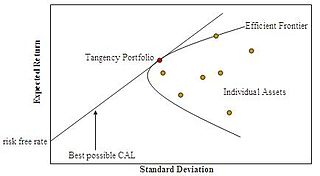
In modern portfolio theory, the efficient frontier is an investment portfolio which occupies the "efficient" parts of the risk–return spectrum. Formally, it is the set of portfolios which satisfy the condition that no other portfolio exists with a higher expected return but with the same standard deviation of return. The efficient frontier was first formulated by Harry Markowitz in 1952; see Markowitz model.
In portfolio theory, a mutual fund separation theorem, mutual fund theorem, or separation theorem is a theorem stating that, under certain conditions, any investor's optimal portfolio can be constructed by holding each of certain mutual funds in appropriate ratios, where the number of mutual funds is smaller than the number of individual assets in the portfolio. Here a mutual fund refers to any specified benchmark portfolio of the available assets. There are two advantages of having a mutual fund theorem. First, if the relevant conditions are met, it may be easier for an investor to purchase a smaller number of mutual funds than to purchase a larger number of assets individually. Second, from a theoretical and empirical standpoint, if it can be assumed that the relevant conditions are indeed satisfied, then implications for the functioning of asset markets can be derived and tested.
Philippe J.S. De Brouwer is a European investment and banking professional as well as academician in finance and investing. As a scientist he is mostly known for his solution to the Fallacy of Large Numbers and his formulation of the Maslowian Portfolio Theory in the field of investment advice.
In finance, the Markowitz model ─ put forward by Harry Markowitz in 1952 ─ is a portfolio optimization model; it assists in the selection of the most efficient portfolio by analyzing various possible portfolios of the given securities. Here, by choosing securities that do not 'move' exactly together, the HM model shows investors how to reduce their risk. The HM model is also called mean-variance model due to the fact that it is based on expected returns (mean) and the standard deviation (variance) of the various portfolios. It is foundational to Modern portfolio theory.
References
- ↑ Michaud, Richard O. (2002). "An Introduction to Resampled Efficiency" (PDF). New Frontier Advisors.
- ↑ Markowitz, H. (1959). Portfolio Selection: Efficient Diversification of Investments. New York: Wiley, 2nd ed. Cambridge, MA: Basil Blackwell, 1991.
- ↑ Sharpe, W. (2009). CFA Portfolio Management, Level III. Vol. 3. Pearson Publishing. p. 261 & 262. ISBN 978-0-536-53718-8.
- ↑ Michaud, R. (2008). Efficient Asset Management: A practical Guide to Stock Portfolio Optimization and Asset Allocation. Boston: Harvard Business School Press. 2nd ed. Oxford: Oxford University Press. ISBN 978-0-19-533191-2.