Resolution proof reduction via local context rewriting

Last updated January 17, 2024

In proof theory, an area of mathematical logic, resolution proof reduction via local context rewriting is a technique for resolution proof reduction via local context rewriting.^[1] This proof compression method was presented as an algorithm named ReduceAndReconstruct, that operates as a post-processing of resolution proofs.

ReduceAndReconstruct is based on a set of local proof rewriting rules that transform a subproof into an equivalent or stronger one.^[1] Each rule is defined to match a specific context.

A context^[1] involves two pivots ( $p$ and $q$ ) and five clauses ( $\alpha$ , $\beta$ , $\gamma$ , $\delta$ and $\eta$ ). The structure of a context is shown in ( 1 ). Note that this implies that $p$ is contained in $\beta$ and $\gamma$ (with opposite polarity) and $q$ is contained in $\delta$ and $\alpha$ (also with opposite polarity).

{\cfrac {{\cfrac {\beta \qquad \gamma }{\delta }}\,p\qquad \alpha }{\eta }}\,q

(1)

The table below shows the rewriting rules proposed by Simone et al..^[1] The idea of the algorithm is to reduce proof size by opportunistically applying these rules.

Context	Rule
Case A1: $s\notin \alpha ,t\in \gamma$	${\cfrac {{\cfrac {stC\qquad {\overline {s}}tD}{tCD}}\,\operatorname {var} (s)\qquad {\overline {t}}E}{CDE}}\,\operatorname {var} (t)\Rightarrow {\cfrac {{\cfrac {stC\qquad {\overline {t}}E}{sCE}}\,\operatorname {var} (t)\qquad {\cfrac {{\overline {t}}E\qquad {\overline {s}}tD}{{\overline {s}}DE}}\,\operatorname {var} (t)}{CDE}}\,\operatorname {var} (s)$
Case A2: $s\notin \alpha ,t\notin \gamma$	${\cfrac {{\cfrac {stC\qquad {\overline {s}}D}{tCD}}\,\operatorname {var} (s)\qquad {\overline {t}}E}{CDE}}\,\operatorname {var} (t)\Rightarrow {\cfrac {{\cfrac {stC\qquad {\overline {t}}E}{sCE}}\,\operatorname {var} (t)\qquad {\overline {s}}D}{CDE}}\,\operatorname {var} (s)$
Case B1: $s\in \alpha ,t\in \gamma$	${\cfrac {{\cfrac {stC\qquad {\overline {s}}tD}{tCD}}\,\operatorname {var} (s)\qquad s{\overline {t}}E}{sCDE}}\,\operatorname {var} (t)\Rightarrow {\cfrac {stC\qquad s{\overline {t}}E}{sCE}}\,\operatorname {var} (t)$
Case B2: $s\in \alpha ,t\notin \gamma$	${\cfrac {{\cfrac {stC\qquad {\overline {s}}D}{tDC}}\,\operatorname {var} (s)\qquad s{\overline {t}}E}{sCDE}}\,\operatorname {var} (t)\Rightarrow {\cfrac {{\cfrac {stC\qquad s{\overline {t}}E}{sCE}}\,\operatorname {var} (t)\qquad {\overline {s}}D}{CDE}}\,\operatorname {var} (s)$
Case B3: ${\overline {s}}\in \alpha ,t\notin \gamma$	${\cfrac {{\cfrac {stC\qquad {\overline {s}}D}{tDC}}\,\operatorname {var} (s)\qquad {\overline {s}}{\overline {t}}E}{{\overline {s}}CDE}}\,\operatorname {var} (t)\Rightarrow {\overline {s}}D$
Case A1'	${\cfrac {{\cfrac {stC\qquad {\overline {s}}tD}{tCD}}\,\operatorname {var} (s)\qquad {\overline {t}}E}{CDE}}\,\operatorname {var} (t)\Leftarrow {\cfrac {{\cfrac {stC\qquad {\overline {t}}E}{sCE}}\,\operatorname {var} (t)\qquad {\cfrac {{\overline {t}}E\qquad {\overline {s}}tD}{{\overline {s}}DE}}\,\operatorname {var} (t)}{CDE}}\,\operatorname {var} (s)$
Case B2': $t\notin \gamma$	${\cfrac {{\cfrac {stC\qquad {\overline {s}}D}{tCD}}\,\operatorname {var} (s)\qquad s{\overline {t}}E}{sCDE}}\,\operatorname {var} (t)\Rightarrow {\cfrac {stC\qquad s{\overline {t}}E}{sCE}}\,\operatorname {var} (t)$

The first five rules were introduced in an earlier paper.^[2] In addition:

Rule A2 does not perform any reduction on its own. However, it is still useful, because of its "shuffling" effect that can create new opportunities for applying the other rules;
Rule A1 is not used in practice, because it may increase proof size;
Rules B1, B2, B2' and B3 are directly responsible for the reduction, as they produce a transformed root clause stronger than the original one;
The application of a B rule may lead to an illegal proof (see the example below), as some literals missing in the transformed root clause may be involved in another resolution step along the path to the proof root. Therefore, the algorithm also has to "reconstruct" a legal proof when this happen.

The following example^[1] shows a situation where the proof becomes illegal after the application of B2' rule:

{\cfrac {{\cfrac {{\cfrac {{\cfrac {\mathbf {pq} \qquad \mathbf {{\overline {p}}o} }{\mathbf {qo} }}\,p\qquad \mathbf {p{\overline {q}}} }{\mathbf {po} }}\,q\qquad {\cfrac {qr\qquad {\overline {p}}{\overline {q}}}{{\overline {p}}r}}\,q}{or}}\,p\qquad {\overline {o}}s}{rs}}\,o

(2)

Applying rule B2' to the highlighted context:

{\cfrac {{\cfrac {{\cfrac {\mathbf {pq} \qquad \mathbf {p{\overline {q}}} }{\mathbf {p} }}\,q\qquad {\cfrac {qr\qquad {\overline {p}}{\overline {q}}}{{\overline {p}}r}}\,q}{or}}\,p\qquad {\overline {o}}s}{rs}}\,o

(3)

The proof is now illegal because the literal $o$ is missing from the transformed root clause. To reconstruct the proof, one can remove $o$ together with the last resolution step (that is now redundant). The final result is the following legal (and stronger) proof:

{\cfrac {{\cfrac {pq\qquad p{\overline {q}}}{p}}\,q\qquad {\cfrac {qr\qquad {\overline {p}}{\overline {q}}}{{\overline {p}}r}}\,q}{r}}\,p

(4)

A further reduction of this proof by applying rule A2 to create a new opportunity to apply rule B2'.^[1]

There are usually a huge number of contexts where rule A2 may be applied, so an exhaustive approach is not feasible in general. One proposal^[1] is to execute ReduceAndReconstruct as a loop with two termination criteria: number of iterations and a timeout (what is reached first). The pseudocode^[1] below shows this.

 1  function ReduceAndReconstruct( $\pi$ /* a proof */, timelimit, maxIterations):  2      for i = 1 to maxIterationsdo  3          ReduceAndReconstructLoop();  4          iftime > timelimitthen// timeout  5              break;  6      end for  7  end function

ReduceAndReconstruct uses the function ReduceAndReconstructLoop, which is specified below. The first part of the algorithm does a topological ordering of the resolution graph (considering that edges goes from antecedentes to resolvents). This is done to ensure that each node is visited after its antecedents (this way, broken resolution steps are always found and fixed).^[1]

 1  function ReduceAndReconstructLoop( $\pi$ /* a proof */):  2      TS = TopologicalSorting( $\pi$ );  3      for each node  $n$ inTS  4          if $n$  is not a leaf  5              if $n_{\text{piv}}\in n_{\text{clause}}^{\text{left}}$  and  ${\overline {n_{\text{piv}}}}\in n_{\text{clause}}^{\text{right}}$ then  6                   $n_{\text{clause}}$  = Resolution( $n_{\text{clause}}^{\text{left}}$ ,  $n_{\text{clause}}^{\text{right}}$ );  7                  Determine left context of  $n$ , if any;  8                  Determine right context of  $n$ , if any;  9                  Heuristically choose one context (if any) and apply the corresponding rule; 10              else if $n_{\text{piv}}\notin n_{\text{clause}}^{\text{left}}$  and  ${\overline {n_{\text{piv}}}}\in n_{\text{clause}}^{\text{right}}$ then 11                  Substitute  $n$  with  $n^{\text{left}}$ ; 12              else if $n_{\text{piv}}\in n_{\text{clause}}^{\text{left}}$  and  ${\overline {n_{\text{piv}}}}\notin n_{\text{clause}}^{\text{right}}$ then 13                  Substitute  $n$  with  $n^{\text{right}}$ ; 14              else if $n_{\text{piv}}\notin n_{\text{clause}}^{\text{left}}$  and  ${\overline {n_{\text{piv}}}}\notin n_{\text{clause}}^{\text{right}}$ then 15                  Heuristically choose an antecedent  $n^{\text{left}}$  or  $n^{\text{right}}$ ; 16                  Substitute  $n$  with  $n^{\text{left}}$  or  $n^{\text{right}}$ ; 17      end for 18  end function

If the input proof is not a tree (in general, resolution graphs are directed acyclic graphs), then the clause $\delta$ of a context may be involved in more than one resolution step. In this case, to ensure that an application of a rewriting rule is not going to interfere with other resolution steps, a safe solution is to create a copy of the node represented by clause $\delta$ .^[1] This solution increases proof size and some caution is needed when doing this.

The heuristic for rule selection is important to achieve a good compression performance. Simone et al.^[1] use the following order of preference for the rules (if applicable to the given context): B2 > B3 > { B2', B1 } > A1' > A2 (X > Y means that X is preferred over Y).

Experiments have shown that ReduceAndReconstruct alone has a worse compression/time ratio than the algorithm RecyclePivots.^[3] However, while RecyclePivots can be applied only once to a proof, ReduceAndReconstruct may be applied multiple times to produce a better compression. An attempt to combine ReduceAndReconstruct and RecyclePivots algorithms has led to good results.^[1]

Notes

1 2 3 4 5 6 7 8 9 10 11 12 Simone, S.F.; Brutomesso, R.; Sharygina, N. "An Efficient and Flexible Approach to Resolution Proof Reduction". 6th Haifa Verification Conference, 2010.
↑ Bruttomesso, R.; Rollini, S.; Sharygina, N.; Tsitovich, A. "Flexible Interpolation with Local Proof Transformations". The International Conference on Computer-Aided Design, 2010.
↑ Bar-Ilan, O.; Fuhrmann, O.; Hoory, S.; Shacham, O.; Strichman, O. "Linear-Time Reductions of Resolution Proofs". HVC, 2008.

Related Research Articles

In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form

In formal language theory, a context-free language (CFL) is a language generated by a context-free grammar (CFG).

Minmax is a decision rule used in artificial intelligence, decision theory, game theory, statistics, and philosophy for minimizing the possible loss for a worst case scenario. When dealing with gains, it is referred to as "maximin" – to maximize the minimum gain. Originally formulated for several-player zero-sum game theory, covering both the cases where players take alternate moves and those where they make simultaneous moves, it has also been extended to more complex games and to general decision-making in the presence of uncertainty.

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.

In vector calculus, Green's theorem relates a line integral around a simple closed curve $C$ to a double integral over the plane region $D$ bounded by $C$ . It is the two-dimensional special case of Stokes' theorem.

The Knuth–Bendix completion algorithm is a semi-decision algorithm for transforming a set of equations into a confluent term rewriting system. When the algorithm succeeds, it effectively solves the word problem for the specified algebra.

The Lenstra–Lenstra–Lovász (LLL) lattice basis reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982. Given a basis $with n -dimensional integer coordinates, for a lattice L with, the LLL algorithm calculates an LLL-reduced lattice basis in time$

In probability theory, if a large number of events are all independent of one another and each has probability less than 1, then there is a positive probability that none of the events will occur. The Lovász local lemma allows one to relax the independence condition slightly: As long as the events are "mostly" independent from one another and aren't individually too likely, then there will still be a positive probability that none of them occurs. It is most commonly used in the probabilistic method, in particular to give existence proofs.

In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation-complete theorem-proving technique for sentences in propositional logic and first-order logic. For propositional logic, systematically applying the resolution rule acts as a decision procedure for formula unsatisfiability, solving the Boolean satisfiability problem. For first-order logic, resolution can be used as the basis for a semi-algorithm for the unsatisfiability problem of first-order logic, providing a more practical method than one following from Gödel's completeness theorem.

In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.

In computer science, confluence is a property of rewriting systems, describing which terms in such a system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.

Wick's theorem is a method of reducing high-order derivatives to a combinatorics problem. It is named after Italian physicist Gian-Carlo Wick. It is used extensively in quantum field theory to reduce arbitrary products of creation and annihilation operators to sums of products of pairs of these operators. This allows for the use of Green's function methods, and consequently the use of Feynman diagrams in the field under study. A more general idea in probability theory is Isserlis' theorem.

A formal grammar describes how to form strings from an alphabet of a formal language that are valid according to the language's syntax. A grammar does not describe the meaning of the strings or what can be done with them in whatever context—only their form. A formal grammar is defined as a set of production rules for such strings in a formal language.

In theoretical computer science, the algorithmic Lovász local lemma gives an algorithmic way of constructing objects that obey a system of constraints with limited dependence.

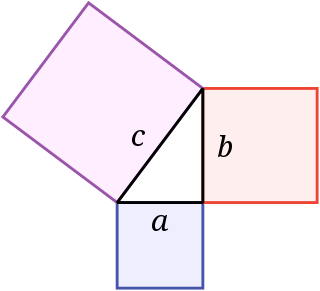
<span class="mw-page-title-main">Pythagorean theorem</span> Relation between sides of a right triangle

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides.

In the theory of quantum communication, the quantum capacity is the highest rate at which quantum information can be communicated over many independent uses of a noisy quantum channel from a sender to a receiver. It is also equal to the highest rate at which entanglement can be generated over the channel, and forward classical communication cannot improve it. The quantum capacity theorem is important for the theory of quantum error correction, and more broadly for the theory of quantum computation. The theorem giving a lower bound on the quantum capacity of any channel is colloquially known as the LSD theorem, after the authors Lloyd, Shor, and Devetak who proved it with increasing standards of rigor.

In proof theory, an area of mathematical logic, proof compression is the problem of algorithmically compressing formal proofs. The developed algorithms can be used to improve the proofs generated by automated theorem proving tools such as SAT solvers, SMT-solvers, first-order theorem provers and proof assistants.

In mathematical logic, proof compression by splitting is an algorithm that operates as a post-process on resolution proofs. It was proposed by Scott Cotton in his paper "Two Techniques for Minimizing Resolution Proof".

In mathematical logic, proof compression by RecycleUnits is a method for compressing propositional logic resolution proofs. Its main idea is to make use of intermediate proof results being unit clauses, i.e. clauses containing only one literal. Certain proof nodes can be replaced with the nodes representing these unit clauses. After this operation the obtained graph is transformed into a valid proof. The output proof is shorter than the original while being equivalent or stronger.

In proof compression LowerUnits (LU) is an algorithm used to compress propositional logic resolution proofs. The main idea of LowerUnits is to exploit the following fact:

Theorem: Let  $be a potentially redundant proof, and be the redundant proof | redundant node. If ’s clause is a unit clause, then is redundant.$

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Simone-1] 1 2 3 4 5 6 7 8 9 10 11 12 Simone, S.F.; Brutomesso, R.; Sharygina, N. "An Efficient and Flexible Approach to Resolution Proof Reduction". 6th Haifa Verification Conference, 2010.

[Bruttomesso-2] Bruttomesso, R.; Rollini, S.; Sharygina, N.; Tsitovich, A. "Flexible Interpolation with Local Proof Transformations". The International Conference on Computer-Aided Design, 2010.

[Bar-Ilan-3] Bar-Ilan, O.; Fuhrmann, O.; Hoory, S.; Shacham, O.; Strichman, O. "Linear-Time Reductions of Resolution Proofs". HVC, 2008.

[1]

[2]

[3]