Problem Representation
In propositional logic a resolution proof of a clause  from a set of clauses C is a directed acyclic graph (DAG): the input nodes are axiom inferences (without premises) whose conclusions are elements of C, the resolvent nodes are resolution inferences, and the proof has a node with conclusion
from a set of clauses C is a directed acyclic graph (DAG): the input nodes are axiom inferences (without premises) whose conclusions are elements of C, the resolvent nodes are resolution inferences, and the proof has a node with conclusion  . [1]
. [1]
The DAG contains an edge from a node  to a node
to a node  if and only if a premise of
if and only if a premise of  is the conclusion of
is the conclusion of  . In this case,
. In this case,  is a child of
is a child of  , and
, and  is a parent of
is a parent of  . A node with no children is a root.
. A node with no children is a root.
A proof compression algorithm will try to create a new DAG with fewer nodes that represents a valid proof of  or, in some cases, a valid proof of a subset of
or, in some cases, a valid proof of a subset of  .
.
A simple example
Let's take a resolution proof for the clause  from the set of clauses
from the set of clauses

Here we can see:
 and
and  are input nodes.
are input nodes.- The node
 has a pivot
has a pivot  ,
, - left resolved literal

- right resolved literal

 conclusion is the clause
conclusion is the clause 
 premises are the conclusion of nodes
premises are the conclusion of nodes  and
and  (its parents)
(its parents)- The DAG would be

 and
and  are parents of
are parents of 
 is a child of
is a child of  and
and 
 is a root of the proof
is a root of the proof
A (resolution) refutation of C is a resolution proof of  from C. It is a common given a node
from C. It is a common given a node  , to refer to the clause
, to refer to the clause  or
or  ’s clause meaning the conclusion clause of
’s clause meaning the conclusion clause of  , and (sub)proof
, and (sub)proof  meaning the (sub)proof having
meaning the (sub)proof having  as its only root.
as its only root.
In some works can be found an algebraic representation of resolution inferences. The resolvent of  and
and  with pivot
with pivot  can be denoted as
can be denoted as  . When the pivot is uniquely defined or irrelevant, we omit it and write simply
. When the pivot is uniquely defined or irrelevant, we omit it and write simply  . In this way, the set of clauses can be seen as an algebra with a commutative operator; and terms in the corresponding term algebra denote resolution proofs in a notation style that is more compact and more convenient for describing resolution proofs than the usual graph notation.
. In this way, the set of clauses can be seen as an algebra with a commutative operator; and terms in the corresponding term algebra denote resolution proofs in a notation style that is more compact and more convenient for describing resolution proofs than the usual graph notation.
In our last example the notation of the DAG would be  or simply
or simply 
We can identify  .
.
Freiling's axiom of symmetry is a set-theoretic axiom proposed by Chris Freiling. It is based on intuition of Stuart Davidson but the mathematics behind it goes back to Wacław Sierpiński.

In proof theory, the semantic tableau is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic. An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation-complete theorem-proving technique for sentences in propositional logic and first-order logic. For propositional logic, systematically applying the resolution rule acts as a decision procedure for formula unsatisfiability, solving the Boolean satisfiability problem. For first-order logic, resolution can be used as the basis for a semi-algorithm for the unsatisfiability problem of first-order logic, providing a more practical method than one following from Gödel's completeness theorem.
In theoretical physics, a source field is a background field coupled to the original field as
SLD resolution is the basic inference rule used in logic programming. It is a refinement of resolution, which is both sound and refutation complete for Horn clauses.

Spinodal decomposition is a mechanism by which a single thermodynamic phase spontaneously separates into two phases. Decomposition occurs when there is no thermodynamic barrier to phase separation. As a result, phase separation via decomposition does not require the nucleation events resulting from thermodynamic fluctuations, which normally trigger phase separation.
In number theory, the fundamental lemma of sieve theory is any of several results that systematize the process of applying sieve methods to particular problems. Halberstam & Richert write:
A curious feature of sieve literature is that while there is frequent use of Brun's method there are only a few attempts to formulate a general Brun theorem ; as a result there are surprisingly many papers which repeat in considerable detail the steps of Brun's argument.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Since the 8th and 9th centuries, the sine and other trigonometric functions have been used in Islamic mathematics and astronomy, reforming the production of sine tables. Khwarizmi and Habash al-Hasib later produced a set of trigonometric tables.
In proof theory, an area of mathematical logic, resolution proof reduction via local context rewriting is a technique for resolution proof reduction via local context rewriting. This proof compression method was presented as an algorithm named ReduceAndReconstruct, that operates as a post-processing of resolution proofs.
In mathematical logic, proof compression by splitting is an algorithm that operates as a post-process on resolution proofs. It was proposed by Scott Cotton in his paper "Two Techniques for Minimizing Resolution Proof".
In mathematical logic, proof compression by RecycleUnits is a method for compressing propositional logic resolution proofs. Its main idea is to make use of intermediate proof results being unit clauses, i.e. clauses containing only one literal. Certain proof nodes can be replaced with the nodes representing these unit clauses. After this operation the obtained graph is transformed into a valid proof. The output proof is shorter than the original while being equivalent or stronger.
In proof compression LowerUnits (LU) is an algorithm used to compress propositional logic resolution proofs. The main idea of LowerUnits is to exploit the following fact:
Theorem: Let be a potentially redundant proof, and be the redundant proof | redundant node. If ’s clause is a unit clause, then is redundant.
In mathematical logic, a redundant proof is a proof that has a subset that is a shorter proof of the same result. In other words, a proof is redundant if it has more proof steps than are actually necessary to prove the result. Formally, a proof of is considered redundant if there exists another proof of such that and where is the number of nodes in .
Exponential Tilting (ET), Exponential Twisting, or Exponential Change of Measure (ECM) is a distribution shifting technique used in many parts of mathematics. The different exponential tiltings of a random variable is known as the natural exponential family of .
In Einstein's theory of general relativity, the interior Schwarzschild metric is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric.
A proper reference frame in the theory of relativity is a particular form of accelerated reference frame, that is, a reference frame in which an accelerated observer can be considered as being at rest. It can describe phenomena in curved spacetime, as well as in "flat" Minkowski spacetime in which the spacetime curvature caused by the energy–momentum tensor can be disregarded. Since this article considers only flat spacetime—and uses the definition that special relativity is the theory of flat spacetime while general relativity is a theory of gravitation in terms of curved spacetime—it is consequently concerned with accelerated frames in special relativity.
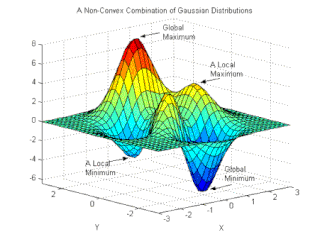
Stochastic gradient Langevin dynamics (SGLD) is an optimization and sampling technique composed of characteristics from Stochastic gradient descent, a Robbins–Monro optimization algorithm, and Langevin dynamics, a mathematical extension of molecular dynamics models. Like stochastic gradient descent, SGLD is an iterative optimization algorithm which uses minibatching to create a stochastic gradient estimator, as used in SGD to optimize a differentiable objective function. Unlike traditional SGD, SGLD can be used for Bayesian learning as a sampling method. SGLD may be viewed as Langevin dynamics applied to posterior distributions, but the key difference is that the likelihood gradient terms are minibatched, like in SGD. SGLD, like Langevin dynamics, produces samples from a posterior distribution of parameters based on available data. First described by Welling and Teh in 2011, the method has applications in many contexts which require optimization, and is most notably applied in machine learning problems.
In mathematics, Rathjen's psi function is an ordinal collapsing function developed by Michael Rathjen. It collapses weakly Mahlo cardinals to generate large countable ordinals. A weakly Mahlo cardinal is a cardinal such that the set of regular cardinals below is closed under . Rathjen uses this to diagonalise over the weakly inaccessible hierarchy.
Cubic equations of state are a specific class of thermodynamic models for modeling the pressure of a gas as a function of temperature and density and which can be rewritten as a cubic function of the molar volume.





















