An acid dissociation constant, Ka, is a quantitative measure of the strength of an acid in solution. It is the equilibrium constant for a chemical reaction
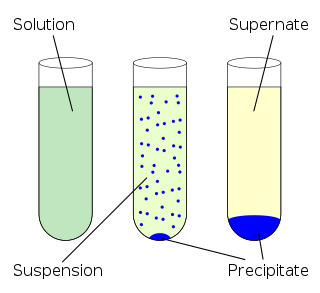
In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.
In chemical thermodynamics, activity is a measure of the "effective concentration" of a species in a mixture, in the sense that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution. The term "activity" in this sense was coined by the American chemist Gilbert N. Lewis in 1907.
In chemistry, the law of mass action is the proposition that the rate of the chemical reaction is directly proportional to the product of the activities or concentrations of the reactants. It explains and predicts behaviors of solutions in dynamic equilibrium. Specifically, it implies that for a chemical reaction mixture that is in equilibrium, the ratio between the concentration of reactants and products is constant.
A partial charge is a non-integer charge value when measured in elementary charge units. Partial charge is more commonly called net atomic charge. It is represented by the Greek lowercase letter 𝛿, namely 𝛿− or 𝛿+.
HSAB concept is a jargon for "hard and soft (Lewis) acids and bases". HSAB is widely used in chemistry for explaining stability of compounds, reaction mechanisms and pathways. It assigns the terms 'hard' or 'soft', and 'acid' or 'base' to chemical species. 'Hard' applies to species which are small, have high charge states, and are weakly polarizable. 'Soft' applies to species which are big, have low charge states and are strongly polarizable.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.

A chemical clock is a complex mixture of reacting chemical compounds in which the onset of an observable property occurs after a predictable induction time due to the presence of clock species at a detectable amount. In cases where one of the reagents has a visible color, crossing a concentration threshold can lead to an abrupt color change after a reproducible time lapse.
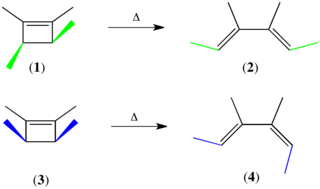
The Woodward–Hoffmann rules, devised by Robert Burns Woodward and Roald Hoffmann, are a set of rules used to rationalize or predict certain aspects of the stereochemistry and activation energy of pericyclic reactions, an important class of reactions in organic chemistry. The rules are best understood in terms of the concept of the conservation of orbital symmetry using orbital correlation diagrams. The Woodward–Hoffmann rules are a consequence of the changes in electronic structure that occur during a pericyclic reaction and are predicated on the phasing of the interacting molecular orbitals. They are applicable to all classes of pericyclic reactions, including (1) electrocyclizations, (2) cycloadditions, (3) sigmatropic reactions, (4) group transfer reactions, (5) ene reactions, (6) cheletropic reactions, and (7) dyotropic reactions. Due to their elegance, simplicity, and generality, the Woodward–Hoffmann rules are credited with first exemplifying the power of molecular orbital theory to experimental chemists.
Marcus theory is a theory originally developed by Rudolph A. Marcus, starting in 1956, to explain the rates of electron transfer reactions – the rate at which an electron can move or jump from one chemical species (called the electron donor) to another (called the electron acceptor). It was originally formulated to address outer sphere electron transfer reactions, in which the two chemical species only change in their charge with an electron jumping (e.g. the oxidation of an ion like Fe2+/Fe3+), but do not undergo large structural changes. It was extended to include inner sphere electron transfer contributions, in which a change of distances or geometry in the solvation or coordination shells of the two chemical species is taken into account (the Fe-O distances in Fe(H2O)2+ and Fe(H2O)3+ are different).

In chemistry, transition state theory (TST) explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.
In the field of computational chemistry, energy minimization is the process of finding an arrangement in space of a collection of atoms where, according to some computational model of chemical bonding, the net inter-atomic force on each atom is acceptably close to zero and the position on the potential energy surface (PES) is a stationary point. The collection of atoms might be a single molecule, an ion, a condensed phase, a transition state or even a collection of any of these. The computational model of chemical bonding might, for example, be quantum mechanics.
In coordination chemistry, a stability constant is an equilibrium constant for the formation of a complex in solution. It is a measure of the strength of the interaction between the reagents that come together to form the complex. There are two main kinds of complex: compounds formed by the interaction of a metal ion with a ligand and supramolecular complexes, such as host–guest complexes and complexes of anions. The stability constant(s) provide(s) the information required to calculate the concentration(s) of the complex(es) in solution. There are many areas of application in chemistry, biology and medicine.
In chemistry, frontier molecular orbital theory is an application of MO theory describing HOMO/LUMO interactions.
In chemistry, solvent effects are the influence of a solvent on chemical reactivity or molecular associations. Solvents can have an effect on solubility, stability and reaction rates and choosing the appropriate solvent allows for thermodynamic and kinetic control over a chemical reaction.
Equilibrium chemistry is concerned with systems in chemical equilibrium. The unifying principle is that the free energy of a system at equilibrium is the minimum possible, so that the slope of the free energy with respect to the reaction coordinate is zero. This principle, applied to mixtures at equilibrium provides a definition of an equilibrium constant. Applications include acid–base, host–guest, metal–complex, solubility, partition, chromatography and redox equilibria.
In chemistry, the Möbius–Hückel treatment is a methodology used to predict whether a reaction is allowed or forbidden. It is often used alone with the Woodward–Hoffmann approach. The description in this article uses the plus-minus sign notation for parity as shorthand while proceeding around a cycle of orbitals in a molecule or system, while the Woodward–Hoffmann methodology uses a large number of rules with the same consequences.
The Baylis–Hillman reaction is a carbon-carbon bond forming reaction between the α-position of an activated alkene and a carbon electrophile such as an aldehyde. Employing a nucleophilic catalyst, such as a tertiary amine and phosphine, this reaction provides a densely functionalized product. It is named for Anthony B. Baylis and Melville E. D. Hillman, two of the chemists who developed this reaction while working at Celanese. This reaction is also known as the Morita–Baylis–Hillman reaction or MBH reaction, as K. Morita had published earlier work on it.
Chemical reaction network theory is an area of applied mathematics that attempts to model the behaviour of real-world chemical systems. Since its foundation in the 1960s, it has attracted a growing research community, mainly due to its applications in biochemistry and theoretical chemistry. It has also attracted interest from pure mathematicians due to the interesting problems that arise from the mathematical structures involved.
In chemistry, catalytic resonance theory was developed to describe the kinetics of reaction acceleration using dynamic catalyst surfaces. Catalytic reactions occurring on surfaces that undergo variation in surface binding energy and/or entropy exhibit overall increase in reaction rate when the surface binding energy frequencies are comparable to the natural frequencies of the surface reaction, adsorption, and desorption.




