The eight queens puzzle is the problem of placing eight chess queens on an 8×8 chessboard so that no two queens threaten each other; thus, a solution requires that no two queens share the same row, column, or diagonal. There are 92 solutions. The problem was first posed in the mid-19th century. In the modern era, it is often used as an example problem for various computer programming techniques.

Derived from the Greek word for '5', and "domino", a pentomino is a polyomino of order 5; that is, a polygon in the plane made of 5 equal-sized squares connected edge to edge. When rotations and reflections are not considered to be distinct shapes, there are 12 different free pentominoes. When reflections are considered distinct, there are 18 one-sided pentominoes. When rotations are also considered distinct, there are 63 fixed pentominoes.

Reversi is a strategy board game for two players, played on an 8×8 uncheckered board. It was invented in 1883. Othello, a variant with a fixed initial setup of the board, was patented in 1971.
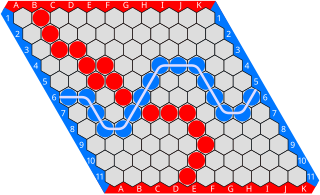
Hex is a two player abstract strategy board game in which players attempt to connect opposite sides of a rhombus-shaped board made of hexagonal cells. Hex was invented by mathematician and poet Piet Hein in 1942 and later rediscovered and popularized by John Nash.

Peg Solitaire, Solo Noble, Solo Goli, Marble Solitaire or simply Solitaire is a board game for one player involving movement of pegs on a board with holes. Some sets use marbles in a board with indentations. The game is known as solitaire in Britain and as peg solitaire in the US where 'solitaire' is now the common name for patience.
A solved game is a game whose outcome can be correctly predicted from any position, assuming that both players play perfectly. This concept is usually applied to abstract strategy games, and especially to games with full information and no element of chance; solving such a game may use combinatorial game theory and/or computer assistance.

A chess problem, also called a chess composition, is a puzzle set by the composer using chess pieces on a chess board, which presents the solver with a particular task. For instance, a position may be given with the instruction that White is to move first, and checkmate Black in two moves against any possible defence. A chess problem fundamentally differs from over-the-board play in that the latter involves a struggle between Black and White, whereas the former involves a competition between the composer and the solver. Most positions which occur in a chess problem unrealistic in the sense that they are very unlikely to occur in over-the-board play. There is a good deal of specialized jargon used in connection with chess problems.

Mastermind or Master Mind is a code-breaking game for two players invented in Israel. It resembles an earlier pencil and paper game called Bulls and Cows that may date back a century.
In the context of combinatorial game theory, which typically studies sequential games with perfect information, a game tree is a graph representing all possible game states within such a game. Such games include well-known ones such as chess, checkers, Go, and tic-tac-toe. This can be used to measure the complexity of a game, as it represents all the possible ways a game can pan out. Due to the large game trees of complex games such as chess, algorithms that are designed to play this class of games will use partial game trees, which makes computation feasible on modern computers. Various methods exist to solve game trees. If a complete game tree can be generated, a deterministic algorithm, such as backward induction or retrograde analysis can be used. Randomized algorithms and minmax algorithms such as MCTS can be used in cases where a complete game tree is not feasible.
The Shannon switching game is a connection game for two players, invented by American mathematician and electrical engineer Claude Shannon, the "father of information theory", some time before 1951. Two players take turns coloring the edges of an arbitrary graph. One player has the goal of connecting two distinguished vertices by a path of edges of their color. The other player aims to prevent this by using their color instead. The game is commonly played on a rectangular grid; this special case of the game was independently invented by American mathematician David Gale in the late 1950s and is known as Gale or Bridg-It.

Connect Four is a game in which the players choose a color and then take turns dropping colored tokens into a six-row, seven-column vertically suspended grid. The pieces fall straight down, occupying the lowest available space within the column. The objective of the game is to be the first to form a horizontal, vertical, or diagonal line of four of one's own tokens. It is therefore a type of m,n,k-game with restricted piece placement. Connect Four is a solved game. The first player can always win by playing the right moves.
Combinatorial game theory measures game complexity in several ways:
- State-space complexity,
- Game tree size,
- Decision complexity,
- Game-tree complexity,
- Computational complexity.

Robot Odyssey is a digital logic game developed by Mike Wallace and Dr. Leslie Grimm and published by The Learning Company in December 1984. It is a sequel to Rocky's Boots, and was released for the Apple II, TRS-80 Color Computer, and MS-DOS. Most players have found it challenging. The player is readying for bed when, suddenly, they fall through the floor into an underground city of robots, Robotropolis. The player begins in the sewers of the city with three programmable robots, and must make their way to the top of the city to try to find their way home again.
God's algorithm is a notion originating in discussions of ways to solve the Rubik's Cube puzzle, but which can also be applied to other combinatorial puzzles and mathematical games. It refers to any algorithm which produces a solution having the fewest possible moves. The allusion to the deity is based on the notion that an omniscient being would know an optimal step from any given configuration.
Computer bridge is the playing of the game contract bridge using computer software. After years of limited progress, since around the end of the 20th century the field of computer bridge has made major advances. In 1996 the American Contract Bridge League (ACBL) established an official World Computer-Bridge Championship, to be held annually along with a major bridge event. The first championship took place in 1997 at the North American Bridge Championships in Albuquerque. Since 1999 the event has been conducted as a joint activity of the American Contract Bridge League and the World Bridge Federation. Alvin Levy, ACBL Board member, initiated this championship and has coordinated the event annually since its inception. The event history, articles and publications, analysis, and playing records can be found at the official website.

Zillions of Games is a commercial general game playing system developed by Jeff Mallett and Mark Lefler in 1998. The game rules are specified with S-expressions, Zillions rule language. It was designed to handle mostly abstract strategy board games or puzzles. After parsing the rules of the game, the system's artificial intelligence can automatically play one or more players. It treats puzzles as solitaire games and its AI can be used to solve them.

Mutant Meeples is a 2012 board game designed by Ted Alspach and published by Beziér Games and Pegasus Spiele. The game has been inspired by Ricochet Robots by Alex Randolph.
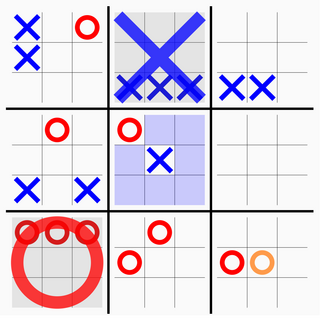
Ultimate tic-tac-toe is a board game composed of nine tic-tac-toe boards arranged in a 3 × 3 grid. Players take turns playing on the smaller tic-tac-toe boards until one of them wins on the larger board. Compared to traditional tic-tac-toe, strategy in this game is conceptually more difficult and has proven more challenging for computers.

Tic-tac-toe is an instance of an m,n,k-game, where two players alternate taking turns on an m×n board until one of them gets k in a row. Harary's generalized tic-tac-toe is an even broader generalization. The game can also be generalized as a nd game. The game can be generalised even further from the above variants by playing on an arbitrary hypergraph where rows are hyperedges and cells are vertices.












