Rigid unit modes

Last updated

Rigid unit modes (RUMs) represent a class of lattice vibrations or phonons that exist in network materials such as quartz, cristobalite or zirconium tungstate. Network materials can be described as three-dimensional networks of polyhedral groups of atoms such as SiO4 tetrahedra or TiO6 octahedra. A RUM is a lattice vibration in which the polyhedra are able to move, by translation and/or rotation, without distorting. RUMs in crystalline materials are the counterparts of floppy modes in glasses, as introduced by Jim Phillips and Mike Thorpe.

Contents

The interest in rigid unit modes

The idea of rigid unit modes was developed for crystalline materials to enable an understanding of the origin of displacive phase transitions in materials such as silicates, which can be described as infinite three-dimensional networks of corner-lined SiO4 and AlO4 tetrahedra. The idea was that rigid unit modes could act as the soft modes for displacive phase transitions.

The original work in silicates showed that many of the phase transitions in silicates could be understood in terms of soft modes that are RUMs.

After the original work on displacive phase transitions, the RUM model was also applied to understanding the nature of the disordered high-temperature phases of materials such as cristobalite, the dynamics and localised structural distortions in zeolites, and negative thermal expansion.

Why rigid unit modes can exist

The simplest way to understand the origin of RUMs is to consider the balance between the numbers of constraints and degrees of freedom of the network, an engineering analysis that dates back to James Clerk Maxwell and which was introduced to amorphous materials by Jim Phillips and Mike Thorpe. If the number of constraints exceeds the number of degrees of freedom, the structure will be rigid. On the other hand, if the number of degrees of freedom exceeds the number of constraints, the structure will be floppy.

For a structure that consists of corner-linked tetrahedra (such as the SiO4 tetrahedra in silica, SiO2) we can count the numbers of constraints and degrees of freedom as follows. For a given tetrahedron, the position of any corner has to have its three spatial coordinates (x,y,z) match the spatial coordinates of the corresponding corner of a linked tetrahedron. Thus each corner has three constraints. These are shared by the two linked tetrahedra, so contribute 1.5 constraints to each tetrahedron. There are 4 corners, so we have a total of 6 constraints per tetrahedron. A rigid three-dimensional object has 6 degrees of freedom, 3 translations and 3 rotations.[ citation needed ] Thus there is an exact balance between the numbers of constraints and degrees of freedom.

(Note that we can get an identical result by considering the atoms to be the basic units. There are 5 atoms in the structural tetrahedron, but 4 of there are shared by two tetrahedra, so that there are 3 + 4*3/2 = 9 degrees of freedom per tetrahedron. The number of constraints to hold together such a tetrahedron is 9 (4 distances and 5 angles)).

What this balance means is that a structure composed of structural tetrahedra joined at corners is exactly on the border between being rigid and floppy. What appears to happen is that symmetry reduces the number of constraints so that structures such as quartz and cristobalite are slightly floppy and thus support some RUMs.

The above analysis can be applied to any network structure composed of polyhedral groups of atoms. One example is the perovskite family of structures, which consist of corner-linked BX6 octahedra such as TiO6 or ZrO6. A simple counting analysis would in fact suggest that such structures are rigid, but in the ideal cubic phase symmetry allows some degree of flexibility. Zirconium tungstate, the archetypal material showing negative thermal expansion, contains ZrO6 octahedra and WO4 tetrahedra, with one of the corners of each WO4 tetrahedra having no linkage. The counting analysis shows that, like silica, zirconium tungstate has an exact balance between the numbers of constraints and degrees of freedom, and further analysis has shown the existence of RUMs in this material.

Related Research Articles

Mineral Element or chemical compound that is normally crystalline formed as a result of geological processes

In geology and mineralogy, a mineral or mineral species is, broadly speaking, a solid chemical compound with a fairly well-defined chemical composition and a specific crystal structure that occurs naturally in pure form.

Silicon Chemical element, symbol Si and atomic number 14

Silicon is a chemical element with the symbol Si and atomic number 14. It is a hard, brittle crystalline solid with a blue-grey metallic luster, and is a tetravalent metalloid and semiconductor. It is a member of group 14 in the periodic table: carbon is above it; and germanium, tin, lead, and flerovium are below it. It is relatively unreactive. Because of its high chemical affinity for oxygen, it was not until 1823 that Jöns Jakob Berzelius was first able to prepare it and characterize it in pure form. Its oxides form a family of anions known as silicates. Its melting and boiling points of 1414 °C and 3265 °C, respectively, are the second highest among all the metalloids and nonmetals, being surpassed only by boron. Silicon is the eighth most common element in the universe by mass, but very rarely occurs as the pure element in the Earth's crust. It is most widely distributed in space in cosmic dusts, planetoids, and planets as various forms of silicon dioxide (silica) or silicates. More than 90% of the Earth's crust is composed of silicate minerals, making silicon the second most abundant element in the Earth's crust, after oxygen. Silicon is a natural element, and when not previously present has a residence time of about 400 years in the world's oceans.

Silicate Class of chemical compounds

In chemistry, a silicate is any member of a family of anions consisting of silicon and oxygen, usually with the general formula [SiO(4−2x)−
4−x]
n, where 0 ≤ x < 2. The family includes orthosilicate SiO4−
4, metasilicate SiO2−
3, and pyrosilicate Si
2O6−
7. The name is also used for any salt of such anions, such as sodium metasilicate; or any ester containing the corresponding chemical group, such as tetramethyl orthosilicate.

An oxyanion, or oxoanion, is an ion with the generic formula A
xOz−
y. Oxyanions are formed by a large majority of the chemical elements. The formulae of simple oxyanions are determined by the octet rule. The corresponding oxyacid of an oxyanion is the compound H
zA
xO
y. The structures of condensed oxyanions can be rationalized in terms of AOn polyhedral units with sharing of corners or edges between polyhedra. The oxyanions adenosine monophosphate (AMP), adenosine diphosphate (ADP) and adenosine triphosphate (ATP) are important in biology.

Cristobalite Silica mineral, polymorph of quartz

Cristobalite is a mineral polymorph of silica that is formed at very high temperatures. It is used in dentistry as a component of alginate impression materials as well as for making models of teeth.

Silicate mineral Rock-forming minerals with predominantly silicate anions

Silicate minerals are rock-forming minerals made up of silicate groups. They are the largest and most important class of minerals and make up approximately 90 percent of Earth's crust.

Zirconium tungstate Chemical compound

Zirconium tungstate (ZrWO4) is the zirconium salt of tungstic acid and has unusual properties. The phase formed at ambient pressure by reaction of ZrO2 and WO3 is a metastable cubic phase, which has negative thermal expansion characteristics, namely it shrinks over a wide range of temperatures when heated. In contrast to most other ceramics exhibiting negative CTE (coefficient of thermal expansion), the CTE of ZrW2O8 is isotropic and has a large negative magnitude (average CTE of -7.2x10−6K−1) over a wide range of temperature (-273 °C to 777 °C). A number of other phases are formed at high pressures.

In condensed matter physics, the term geometrical frustration refers to a phenomenon where atoms tend to stick to non-trivial positions or where, on a regular crystal lattice, conflicting inter-atomic forces lead to quite complex structures. As a consequence of the frustration in the geometry or in the forces, a plenitude of distinct ground states may result at zero temperature, and usual thermal ordering may be suppressed at higher temperatures. Much studied examples are amorphous materials, glasses, or dilute magnets.

Tetrahedral molecular geometry Central atom with four substituents located at the corners of a tetrahedron

In a tetrahedral molecular geometry, a central atom is located at the center with four substituents that are located at the corners of a tetrahedron. The bond angles are cos−1(−1⁄3) = 109.4712206...° ≈ 109.5° when all four substituents are the same, as in methane as well as its heavier analogues. Methane and other perfectly symmetrical tetrahedral molecules belong to point group Td, but most tetrahedral molecules have lower symmetry. Tetrahedral molecules can be chiral.

Vanadate Coordination complex of vanadium

In chemistry, a vanadate is an anionic coordination complex of vanadium. Often vanadate refers to oxoanions of vanadium, most of which exist in its highest oxidation state of +5. The complexes [V(CN)6]3- and [V2Cl9]3- are referred to as hexacyanovanadate and nonachlorodivanadate.

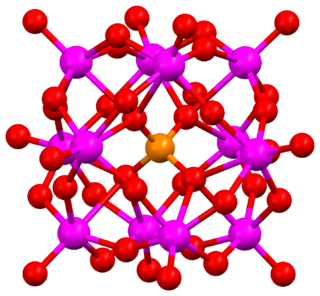
Keggin structure Best known structural form for heteropoly acids

Keggin structure is the best known structural form for heteropoly acids. It is the structural form of α-Keggin anions, which have a general formula of [XM12O40]n−, where X is the heteroatom, M is the addendum atom, and O represents oxygen. The structure self-assembles in acidic aqueous solution and is the most stable structure of polyoxometalate catalysts.

Partheite or parthéite is a calcium aluminium silicate and a member of the zeolite group of minerals, a group of silicates with large open channels throughout the crystal structure, which allow passage of liquids and gasses through the mineral. It was first discovered in 1979 in rodingitic dikes in an ophiolite zone of the Taurus Mountains in southwest Turkey. The second discovery occurred in gabbro-pegmatites in the Ural Mountains, Russia. Since its discovery and naming, the chemical formula for partheite has been revised from CaAl2Si2O8•2H2O to include not only water but hydroxyl groups as well. The framework of the mineral is interrupted due to these hydroxyl groups attaching themselves to aluminum centered oxygen tetrahedra. This type of interrupted framework is known in only one other zeolite, the mineral roggianite. As a silicate based mineral with the properties of a zeolite, partheite was first described as zeolite-like in 1984 and listed as a zeolite in 1985. Partheite and lawsonite are polymorphs. Associated minerals include prehnite, thomsonite, augite, chlorite and tremolite.

Plumbogummite Alunite supergroup, phosphate mineral

Plumbogummite is a rare secondary lead phosphate mineral, belonging to the alunite supergroup of minerals, crandallite subgroup. Some other members of this subgroup are:

Fluor-liddicoatite

Fluor-liddicoatite is a rare member of the tourmaline group of minerals, elbaite subgroup, and the theoretical calcium endmember of the elbaite-fluor-liddicoatite series; the pure end-member has not yet been found in nature. Fluor-liddicoatite is indistinguishable from elbaite by X-ray diffraction techniques. It forms a series with elbaite and probably also with olenite. Liddiocoatite is currently a non-approved mineral name, but Aurisicchio et al. (1999) and Breaks et al. (2008) found OH-dominant species. Formulae are

Vlasovite

Vlasovite is a rare inosilicate (chain silicate) mineral with sodium and zirconium, with the chemical formula Na2ZrSi4O11. It was discovered in 1961 at Vavnbed Mountain in the Lovozero Massif, in the Northern Region of Russia. The researchers who first identified it, R P Tikhonenkova and M E Kazakova, named it for Kuzma Aleksevich Vlasov (1905–1964), a Russian mineralogist and geochemist who studied the Lovozero massif, and who was the founder of the Institute of Mineralogy, Geochemistry, and Crystal Chemistry of Rare Elements, Moscow, Russia.

Structure of liquids and glasses Atomic-scale non-crystalline structure of liquids and glasses

The structure of liquids, glasses and other non-crystalline solids is characterized by the absence of long-range order which defines crystalline materials. Liquids and amorphous solids do, however, possess a rich and varied array of short to medium range order, which originates from chemical bonding and related interactions. Metallic glasses, for example, are typically well described by the dense random packing of hard spheres, whereas covalent systems, such as silicate glasses, have sparsely packed, strongly bound, tetrahedral network structures. These very different structures result in materials with very different physical properties and applications.

Silicon–oxygen tetrahedron

A silicon–oxygen tetrahedron is the SiO4 anionic group, or a silicon atom with four surrounding oxygen atoms arranged to define the corners of a tetrahedron. This is a fundamental component of most silicates in the Earth's crust. A variety of silicate minerals can be identified by the way that the tetrahedra links differ, also by the cations present in the mineral.

Rigidity theory, or topological constraint theory, is a tool for predicting properties of complex networks based on their composition. It was introduced by James Charles Phillips in 1979 and 1981, and refined by Michael Thorpe in 1983. Inspired by the study of the stability of mechanical trusses as pioneered by James Clerk Maxwell, and by the seminal work on glass structure done by William Houlder Zachariasen, this theory reduces complex molecular networks to nodes constrained by rods, thus filtering out microscopic details that ultimately don't affect macroscopic properties. An equivalent theory was developed by P.K. Gupta A.R. Cooper in 1990, where rather than nodes representing atoms, they represented unit polytopes. An example of this would be the SiO tetrahedra in pure glassy silica. This style of analysis has applications in biology and chemistry, such as understanding adaptability in protein-protein interaction networks. Rigidity theory applied to the molecular networks arising from phenotypical expression of certain diseases may provide insights regarding their structure and function.

NASICON

NASICON is an acronym for sodium (Na) Super Ionic CONductor, which usually refers to a family of solids with the chemical formula Na1+xZr2SixP3−xO12, 0 < x < 3. In a broader sense, it is also used for similar compounds where Na, Zr and/or Si are replaced by isovalent elements. NASICON compounds have high ionic conductivities, on the order of 10−3 S/cm, which rival those of liquid electrolytes. They are caused by hopping of Na ions among interstitial sites of the NASICON crystal lattice.

Tumchaite

Tumchaite, Na2(Zr,Sn)Si4O11·H2O, is a colorless to white monoclinic phyllosilicate mineral. It is associated with calcite, dolomite, and pyrite in the late dolomite-calcite carbonatites. It can be transparent to translucent; has a vitreous luster; and has perfect cleavage on {100}. Its hardness is 4.5, between fluorite and apatite. Tumchaite is isotypic with penkvilksite. The structure of the mineral is identified by silicate sheets parallel {100}, formed by alternation of clockwise and counterclockwise growing spiral chains of corner-sharing SiO4 tetrahedra. Tumchaite is named for the river Tumcha near Vuoriyarvi massif.

References

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.